The Condorcet paradox reveals inconsistencies in collective decision-making, where individual preferences can lead to cycles with no clear winner in majority voting. This paradox challenges the idea that majority rule always produces a rational and transitive group choice. Discover how this intriguing phenomenon impacts voting systems and what it means for Your decision-making processes in the full article.
Table of Comparison
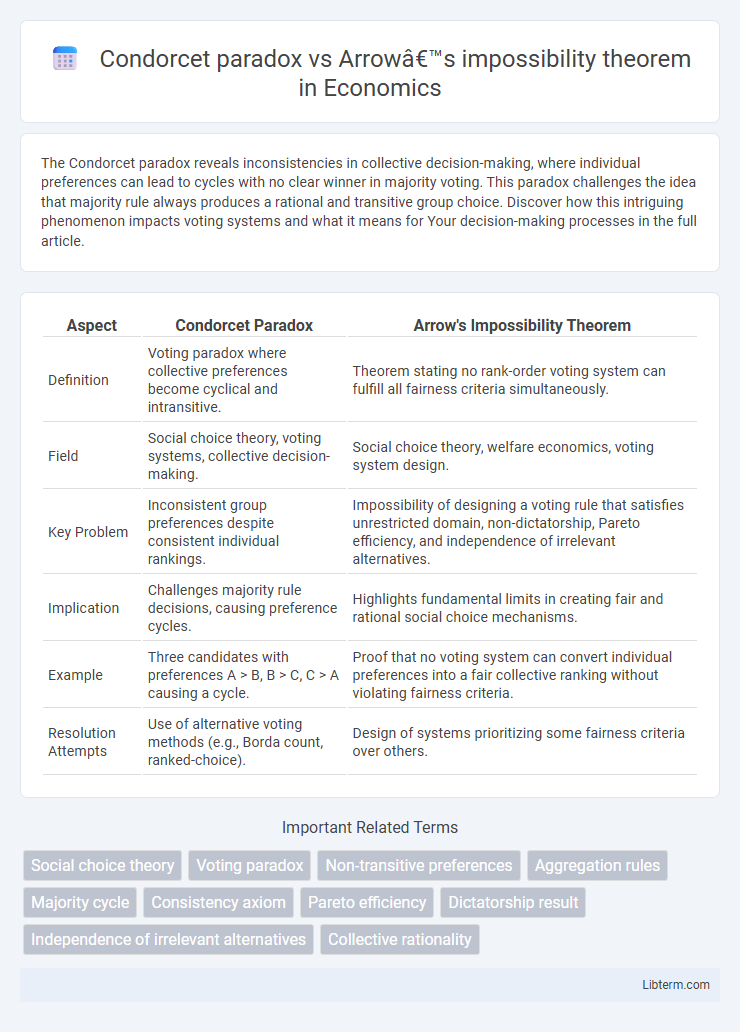
| Aspect | Condorcet Paradox | Arrow's Impossibility Theorem |
|---|---|---|
| Definition | Voting paradox where collective preferences become cyclical and intransitive. | Theorem stating no rank-order voting system can fulfill all fairness criteria simultaneously. |
| Field | Social choice theory, voting systems, collective decision-making. | Social choice theory, welfare economics, voting system design. |
| Key Problem | Inconsistent group preferences despite consistent individual rankings. | Impossibility of designing a voting rule that satisfies unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. |
| Implication | Challenges majority rule decisions, causing preference cycles. | Highlights fundamental limits in creating fair and rational social choice mechanisms. |
| Example | Three candidates with preferences A > B, B > C, C > A causing a cycle. | Proof that no voting system can convert individual preferences into a fair collective ranking without violating fairness criteria. |
| Resolution Attempts | Use of alternative voting methods (e.g., Borda count, ranked-choice). | Design of systems prioritizing some fairness criteria over others. |
Understanding the Condorcet Paradox
The Condorcet paradox occurs when collective preferences become cyclic, meaning no option is preferred by a majority over all others, revealing inconsistencies in majority voting systems. This paradox highlights challenges in aggregating individual voter preferences into a coherent social choice, demonstrating how collective decisions may lack a clear winner even when individual rankings are transitive. Understanding the Condorcet paradox is crucial for grasping the fundamental limits identified by Arrow's impossibility theorem, which proves that no rank-order voting system can simultaneously meet all fairness criteria like unanimity, non-dictatorship, and independence of irrelevant alternatives.
Exploring Arrow’s Impossibility Theorem
Arrow's Impossibility Theorem reveals fundamental limitations in designing a socially fair voting system that simultaneously satisfies unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. This theorem proves that no rank-order voting system can convert individual preferences into a collective decision without violating at least one of these criteria, highlighting intrinsic challenges in collective choice theory. Unlike the Condorcet paradox, which illustrates cyclical majorities in preference aggregation, Arrow's theorem generalizes the impossibility of a perfect social welfare function across all voting methods.
Historical Development of Voting Theory
The historical development of voting theory reveals the Condorcet paradox, identified by Marquis de Condorcet in the 18th century, as a fundamental challenge showing cycles in collective preferences despite individual rationality. Arrow's impossibility theorem, formulated by economist Kenneth Arrow in 1951, extended these insights by proving no voting system can perfectly convert individual preferences into a consistent group decision under certain fairness criteria. These foundational results profoundly influenced social choice theory, highlighting the inherent difficulties in designing fair and rational voting mechanisms.
Key Concepts: Preferences and Collective Choice
The Condorcet paradox illustrates the inconsistency in collective preferences where individual rational choices lead to cyclical majorities without a clear winner. Arrow's impossibility theorem formalizes the limitations of social choice mechanisms by proving no voting system can convert individual preferences into a collective decision while simultaneously satisfying fairness criteria like non-dictatorship, unanimity, and independence of irrelevant alternatives. Both highlight fundamental challenges in aggregating individual preferences into a coherent collective choice, emphasizing unavoidable trade-offs in designing voting methods.
The Mathematical Foundations of the Condorcet Paradox
The Condorcet paradox arises from the non-transitivity of collective preferences in majority voting, demonstrating that individual rationality does not guarantee collective rationality. Its mathematical foundation lies in preference cycles, where pairwise majority votes can produce intransitive social orders, highlighting inconsistencies in aggregating individual rankings. Arrow's impossibility theorem extends these insights by proving no rank-order voting system can simultaneously satisfy fairness criteria such as unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives.
Arrow’s Axioms: Fairness Criteria in Voting
Arrow's impossibility theorem highlights the challenge of designing a voting system that simultaneously satisfies fairness criteria such as unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The Condorcet paradox illustrates situations where collective preferences can cycle inconsistently, violating transitivity and complicating the aggregation of individual preferences into a fair social order. Arrow's axioms formalize fairness standards that no rank-order voting system can fully meet, revealing fundamental limitations in achieving a perfectly fair decision-making process.
Comparing Condorcet and Arrow: Core Differences
The Condorcet paradox reveals how collective preferences can become cyclic and intransitive, highlighting inconsistencies in majority voting outcomes. Arrow's impossibility theorem generalizes these issues by proving that no voting system can simultaneously satisfy fairness criteria like non-dictatorship, unanimity, and independence of irrelevant alternatives. The core difference lies in Condorcet's focus on preference cycles in pairwise comparisons, while Arrow addresses the broader challenge of creating a perfect social welfare function under realistic axioms.
Real-world Implications for Democratic Systems
The Condorcet paradox reveals inherent challenges in collective decision-making by demonstrating that majority preferences can become cyclical and inconsistent, undermining the notion of a clear winner in elections. Arrow's impossibility theorem further emphasizes these difficulties by proving that no voting system can perfectly translate individual preferences into a fair and consistent societal choice without violating key fairness criteria. These insights highlight fundamental limitations in democratic systems, prompting the need for carefully designed electoral methods, awareness of voting paradoxes, and continuous reform to enhance representative fairness and stability.
Critiques and Limitations of Each Theory
The Condorcet paradox highlights limitations in majority voting systems by demonstrating that collective preferences can be cyclic and intransitive, which challenges the consistency of social choice outcomes. Arrow's impossibility theorem critiques all voting systems by proving that no rank-order voting method can simultaneously satisfy fairness criteria such as non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. Both theories face critiques for their assumptions; the Condorcet paradox assumes rational voter preferences while Arrow's theorem relies on strict axioms that may not hold in practical scenarios, limiting their real-world applicability.
Future Directions in Social Choice Theory
Future directions in social choice theory explore resolving conflicts highlighted by the Condorcet paradox and Arrow's impossibility theorem through enhanced aggregation methods and algorithmic approaches. Research emphasizes developing preference aggregation models that incorporate machine learning and multi-agent systems to better reflect collective rationality and fairness. Advances in computational social choice aim to design voting rules mitigating cycle inconsistencies and improving social welfare despite inherent theoretical limitations.
Condorcet paradox Infographic
 libterm.com
libterm.com