The Black-Scholes model revolutionized options pricing by providing a mathematical framework to estimate the fair value of European-style options, relying on variables such as stock price, strike price, volatility, time to expiration, and risk-free interest rate. Understanding this model helps you grasp how financial markets assess risk and make trading decisions for derivatives. Explore the rest of the article to uncover the detailed mechanics and applications of the Black-Scholes model.
Table of Comparison
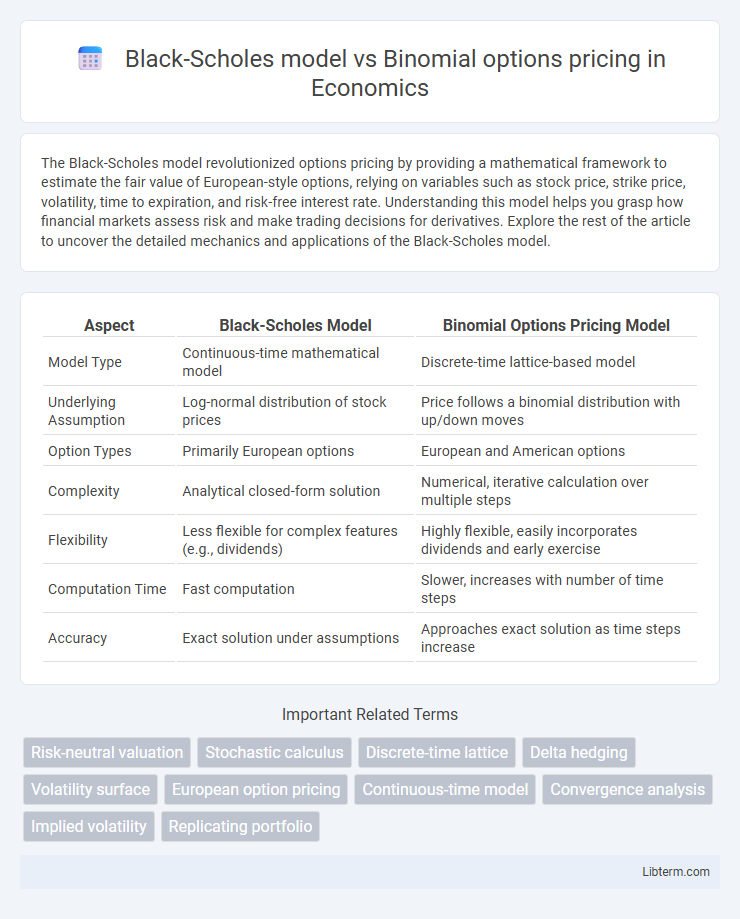
| Aspect | Black-Scholes Model | Binomial Options Pricing Model |
|---|---|---|
| Model Type | Continuous-time mathematical model | Discrete-time lattice-based model |
| Underlying Assumption | Log-normal distribution of stock prices | Price follows a binomial distribution with up/down moves |
| Option Types | Primarily European options | European and American options |
| Complexity | Analytical closed-form solution | Numerical, iterative calculation over multiple steps |
| Flexibility | Less flexible for complex features (e.g., dividends) | Highly flexible, easily incorporates dividends and early exercise |
| Computation Time | Fast computation | Slower, increases with number of time steps |
| Accuracy | Exact solution under assumptions | Approaches exact solution as time steps increase |
Introduction to Options Pricing Models
The Black-Scholes model provides a closed-form analytical solution for European option pricing, relying on assumptions such as constant volatility and lognormal asset price distribution. The Binomial options pricing model uses a discrete-time framework, constructing a price tree to evaluate options under varying market conditions and is adaptable to American options. Both models are fundamental for estimating fair option values but differ in approach, complexity, and flexibility in handling early exercise features.
Overview of the Black-Scholes Model
The Black-Scholes model provides a closed-form analytical solution for pricing European-style options by assuming constant volatility and continuous trading in an efficient market. It relies on partial differential equations to estimate the fair value of call and put options based on parameters such as stock price, strike price, time to expiration, risk-free interest rate, and volatility. In contrast to binomial option pricing, which uses discrete time steps and a recombining price lattice, the Black-Scholes model offers a faster, formula-driven approach but is less flexible for American options or cases with changing volatility.
Fundamentals of the Binomial Options Pricing Model
The Binomial Options Pricing Model fundamentally relies on a discrete-time framework that maps potential future asset prices over multiple periods, enabling precise option valuation through a backward induction process. It models asset price movements as an up or down factor per time step, incorporating risk-neutral probabilities to calculate the expected option payoff under a risk-neutral measure. This approach contrasts with the continuous-time Black-Scholes model by allowing flexibility in handling American options and varying dividend scenarios through a straightforward recombining price lattice.
Key Assumptions in Black-Scholes and Binomial Models
The Black-Scholes model assumes continuous trading, constant volatility, and a lognormal distribution of stock prices, with no dividends paid during the option's life, while the binomial model allows for discrete time steps, varying up and down price movements, and can incorporate dividends and early exercise opportunities. The Black-Scholes framework is built on the premise of a frictionless market without arbitrage and constant risk-free rates, whereas the binomial model relies on a recombining price tree, enabling flexible adjustments to changing market parameters. Both models require assumptions about the underlying asset's price dynamics but differ in their approach to time and exercise features, impacting their applicability to American and European options.
Mathematical Formulation: Black-Scholes vs Binomial
The Black-Scholes model uses a continuous-time stochastic differential equation to derive a closed-form solution for European options pricing, leveraging geometric Brownian motion and the partial differential equation known as the Black-Scholes equation. In contrast, the Binomial options pricing model applies a discrete-time lattice framework, calculating option values through backward induction on a recombining binomial tree, which accommodates American options and varying exercise styles. Black-Scholes assumes constant volatility and risk-free rate, while the Binomial model allows flexibility in modeling changing parameters over multiple time steps.
Practical Applications in Financial Markets
The Black-Scholes model offers a closed-form solution ideal for pricing European options with continuous trading and constant volatility assumptions, making it widely used in equity and index options markets. The Binomial options pricing model provides greater flexibility by accommodating American options and allowing for varying volatility and discrete time intervals, which is crucial for pricing early-exercise options and complex derivatives. Both models are integral to risk management, hedging strategies, and derivative valuation, but practitioners often prefer the Binomial model for its adaptability in dynamic market conditions.
Strengths and Limitations of the Black-Scholes Model
The Black-Scholes model offers analytical simplicity and closed-form solutions for European options, enabling quick and efficient pricing under the assumptions of constant volatility and lognormal asset price distribution. Its limitations include the inability to accurately price American options and the model's sensitivity to volatility estimates, which can lead to mispricing in markets exhibiting stochastic volatility or jumps. Compared to binomial options pricing, which accommodates early exercise and varying parameters through a discrete-time framework, Black-Scholes is less flexible but computationally faster for standard scenarios.
Advantages and Disadvantages of the Binomial Model
The Binomial options pricing model offers greater flexibility in handling American options and complex features such as early exercise and varying dividends, which the Black-Scholes model cannot easily accommodate due to its continuous-time framework. It provides a discrete-time lattice approach that can model multiple exercise dates and path-dependent options, enabling more precise valuations for options with complex payoff structures. However, the Binomial model can be computationally intensive as the number of time steps increases, making it slower and more resource-demanding compared to the closed-form Black-Scholes formula.
Comparative Analysis: Accuracy and Flexibility
The Black-Scholes model offers closed-form solutions ideal for European options with continuous trading assumptions, providing high accuracy in liquid markets but limited flexibility for American options or varying dividend scenarios. The binomial options pricing model employs a discrete-time lattice framework, enabling detailed modeling of American options and complex features such as early exercise and varying dividends, thus enhancing flexibility at the expense of computational intensity. Empirical studies show binomial methods converge to Black-Scholes values with increased steps, highlighting a trade-off between computational cost and precision depending on the option's characteristics.
Choosing the Right Model for Option Valuation
Choosing the right model for option valuation depends on the specific requirements of accuracy, computational complexity, and the option's characteristics. The Black-Scholes model provides a closed-form solution ideal for European options with constant volatility, while the Binomial options pricing model offers greater flexibility by accommodating American options and varying volatility through its discrete-time lattice framework. Analysts often prefer the Binomial model for options with early exercise features and complex payoffs, whereas Black-Scholes remains popular for its speed and simplicity in standard scenarios.
Black-Scholes model Infographic
 libterm.com
libterm.com