The Trinomial Tree Model offers a flexible approach to option pricing by allowing three possible price movements--up, down, or unchanged--at each step, enhancing accuracy compared to binomial models. This method effectively captures the complexities of asset price behavior over discrete intervals, making it valuable for pricing American and exotic options. Explore the rest of the article to understand how the Trinomial Tree Model can optimize your option valuation processes.
Table of Comparison
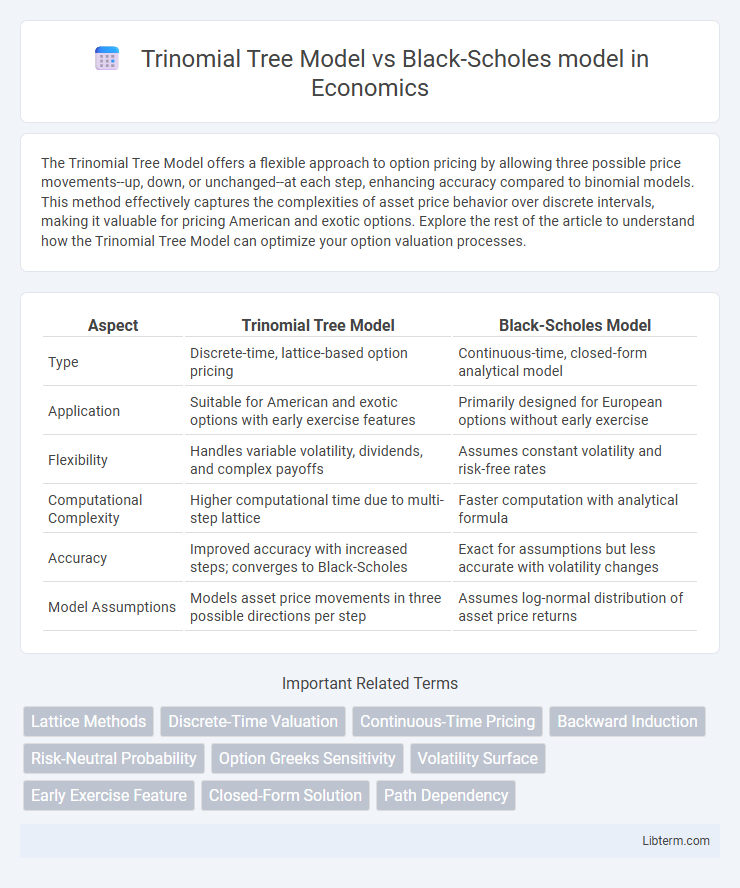
| Aspect | Trinomial Tree Model | Black-Scholes Model |
|---|---|---|
| Type | Discrete-time, lattice-based option pricing | Continuous-time, closed-form analytical model |
| Application | Suitable for American and exotic options with early exercise features | Primarily designed for European options without early exercise |
| Flexibility | Handles variable volatility, dividends, and complex payoffs | Assumes constant volatility and risk-free rates |
| Computational Complexity | Higher computational time due to multi-step lattice | Faster computation with analytical formula |
| Accuracy | Improved accuracy with increased steps; converges to Black-Scholes | Exact for assumptions but less accurate with volatility changes |
| Model Assumptions | Models asset price movements in three possible directions per step | Assumes log-normal distribution of asset price returns |
Introduction to Option Pricing Models
Option pricing models analyze the value of financial derivatives by assessing factors such as underlying asset price, volatility, time to expiration, and risk-free interest rates. The Trinomial Tree Model uses a discrete time lattice allowing three possible price movements at each step, providing flexibility and improved accuracy in capturing complex option features. The Black-Scholes model offers a closed-form solution under continuous-time assumptions and constant volatility, making it computationally efficient for European-style options but less adaptable to early exercise and path-dependent features.
Overview of the Trinomial Tree Model
The Trinomial Tree Model offers a versatile approach to option pricing by discretizing the price movements into three possible states--up, down, and unchanged--at each step, allowing greater accuracy in capturing market fluctuations compared to simpler binomial models. This model accommodates varying volatility and interest rates, making it effective for pricing American options where early exercise is possible. Its iterative structure supports fine-tuning time steps to balance computational efficiency and precision, providing a robust alternative to the continuous-time Black-Scholes model.
Fundamentals of the Black-Scholes Model
The Black-Scholes model, founded on the assumptions of continuous time trading, constant volatility, and log-normal distribution of asset prices, provides a closed-form solution for European option pricing. It employs partial differential equations to evaluate options by modeling the underlying asset's stochastic process as geometric Brownian motion with constant drift and volatility. Unlike the Trinomial Tree Model, which uses discrete time steps to approximate price movements, the Black-Scholes model emphasizes analytic tractability and assumes frictionless markets for risk-neutral valuation.
Underlying Assumptions: Trinomial Tree vs Black-Scholes
The Trinomial Tree Model assumes that the underlying asset price can move to three possible states (up, down, or unchanged) in discrete time intervals, capturing price paths with greater flexibility and allowing for varying volatility and dividend distributions. The Black-Scholes model relies on continuous-time assumptions with lognormal distribution of asset prices, constant volatility, and risk-free interest rates, assuming markets are frictionless and follow geometric Brownian motion. These foundational differences affect option pricing accuracy, with the trinomial tree accommodating more complex market conditions compared to the more restrictive Black-Scholes framework.
Computational Complexity Comparison
The Trinomial Tree Model involves discrete time steps and three possible price movements per step, resulting in computational complexity of O(n^2) for n time increments, making it more intensive for fine-grained simulations. The Black-Scholes Model, based on a closed-form analytical solution, offers constant time complexity O(1) for option pricing but lacks flexibility for American options and path-dependent features. Consequently, the Trinomial Tree Model is preferred for scenarios requiring early exercise features despite higher computational cost, whereas Black-Scholes excels in speed for European-style options.
Accuracy in Pricing American and Exotic Options
The Trinomial Tree Model offers greater accuracy in pricing American and exotic options by explicitly modeling early exercise features and complex payoff structures through discrete time steps. In contrast, the Black-Scholes model assumes continuous trading and constant volatility, limiting its precision for options with path-dependent characteristics or early exercise rights. Consequently, trinomial trees provide a more flexible framework for capturing market realities and option-specific features, enhancing valuation accuracy.
Flexibility in Modeling Volatility and Dividends
The Trinomial Tree Model offers greater flexibility in modeling volatility and dividends by allowing varying volatility at each node and accommodating discrete dividend payments. In contrast, the Black-Scholes model assumes constant volatility and continuous dividend yields, limiting its accuracy in scenarios with fluctuating market conditions or discrete dividends. This adaptability makes the trinomial approach more suitable for pricing complex options with path-dependent features or irregular dividend schedules.
Advantages of the Trinomial Tree Model
The Trinomial Tree Model offers greater flexibility and accuracy in option pricing by incorporating three possible price movements--up, down, and unchanged--at each step, which enhances its ability to model complex payoffs and American-style options with early exercise features. It provides a more fine-grained approximation of the underlying asset's price distribution compared to the Black-Scholes model, which assumes continuous price changes and lognormal distribution but may misprice options with path-dependent or discrete payoff structures. This model's adaptability to various volatility structures and dividend yields makes it superior for scenarios where the Black-Scholes assumptions of constant volatility and risk-free rates do not hold.
Strengths of the Black-Scholes Model
The Black-Scholes model excels in providing closed-form analytical solutions for European option pricing, enabling rapid and precise calculations compared to the iterative nature of the trinomial tree model. It effectively captures option sensitivities such as delta and gamma, facilitating risk management and hedging strategies. The model's assumptions, including constant volatility and lognormal asset price distribution, simplify complexity while providing robust price estimates in stable market conditions.
Choosing the Right Model for Your Needs
Choosing the right option pricing model depends on factors such as asset volatility, time horizon, and computational resources. The Trinomial Tree Model offers greater flexibility for American options and scenarios with complex early exercise features due to its stepwise approach and discrete asset price paths. The Black-Scholes model provides closed-form solutions for European options, favoring computational efficiency and simpler assumptions, making it suitable for standard options without dividends or early exercise.
Trinomial Tree Model Infographic
 libterm.com
libterm.com