Expected Shortfall measures the risk of potential losses in extreme market conditions by estimating the average loss beyond a specified confidence level, providing a more comprehensive risk assessment than Value at Risk. It captures tail risk and is widely used by financial institutions to ensure robust risk management and regulatory compliance. Explore the rest of the article to understand how Expected Shortfall can enhance your portfolio's risk evaluation.
Table of Comparison
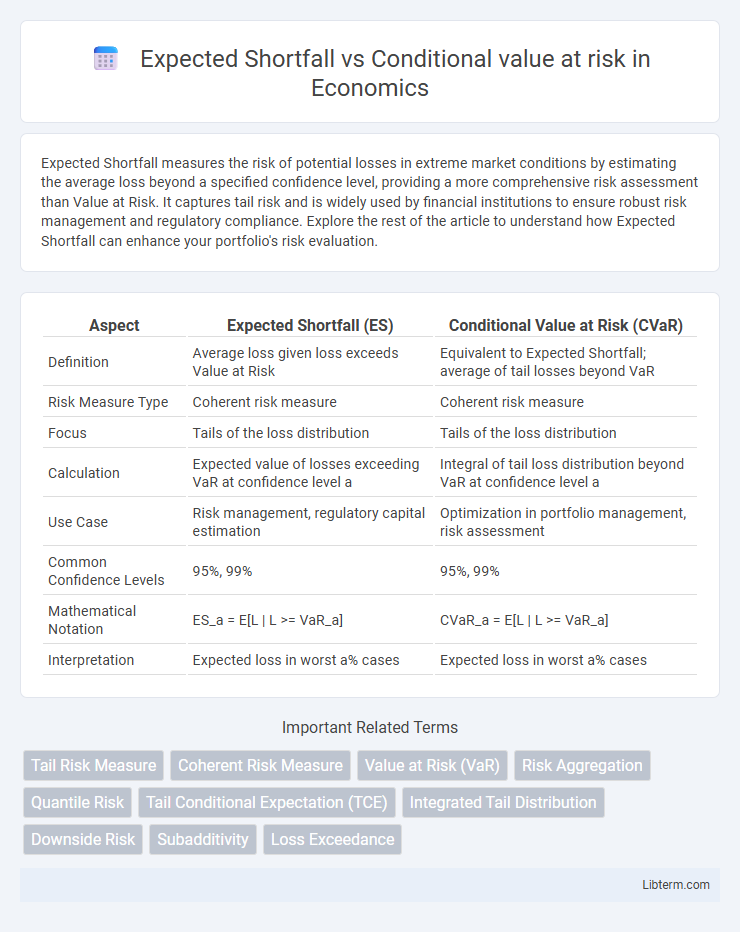
| Aspect | Expected Shortfall (ES) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | Average loss given loss exceeds Value at Risk | Equivalent to Expected Shortfall; average of tail losses beyond VaR |
| Risk Measure Type | Coherent risk measure | Coherent risk measure |
| Focus | Tails of the loss distribution | Tails of the loss distribution |
| Calculation | Expected value of losses exceeding VaR at confidence level a | Integral of tail loss distribution beyond VaR at confidence level a |
| Use Case | Risk management, regulatory capital estimation | Optimization in portfolio management, risk assessment |
| Common Confidence Levels | 95%, 99% | 95%, 99% |
| Mathematical Notation | ES_a = E[L | L >= VaR_a] | CVaR_a = E[L | L >= VaR_a] |
| Interpretation | Expected loss in worst a% cases | Expected loss in worst a% cases |
Introduction to Risk Measures in Finance
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) are coherent risk measures widely used in finance to assess potential losses in portfolios beyond a given confidence level. Both metrics provide insights into tail risk by evaluating the average loss occurring in the worst-case scenarios, improving upon Value at Risk (VaR) by addressing its lack of subadditivity and providing more comprehensive risk assessments. These measures are critical for risk management, regulatory compliance, and capital allocation, particularly under Basel Accords and modern financial risk frameworks.
What is Expected Shortfall?
Expected Shortfall (ES), also known as Conditional Value at Risk (CVaR), measures the average loss in the worst-case percentage of a portfolio's distribution beyond a specified Value at Risk (VaR) threshold. It provides a more comprehensive risk assessment by capturing the tail risk and the magnitude of extreme losses, unlike VaR which only indicates the loss threshold exceeded with a certain probability. Financial institutions and risk managers use Expected Shortfall to better understand potential losses during market stress and improve capital allocation.
Understanding Conditional Value at Risk (CVaR)
Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss exceeding the Value at Risk (VaR) at a given confidence level, providing a more comprehensive assessment of tail risk in financial portfolios. CVaR captures extreme downside risk by averaging outcomes in the worst percentile of a loss distribution, enhancing risk management beyond the VaR's threshold estimate. This risk metric is widely used in portfolio optimization and stress testing to quantify potential severe losses under adverse market conditions.
Historical Background: Evolution of ES and CVaR
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) originated from risk management practices aimed at improving the limitations of Value at Risk (VaR) during the 1990s. ES was initially introduced in the academic literature by Artzner et al. in 1999 as a coherent risk measure addressing VaR's lack of subadditivity, while Rockafellar and Uryasev further developed and popularized CVaR in optimization frameworks during the early 2000s. Both measures evolved to provide more comprehensive assessments of tail risks by accounting for losses beyond the VaR threshold, influencing regulatory standards like Basel III.
Key Differences Between Expected Shortfall and CVaR
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) both measure the tail risk of a loss distribution by focusing on the average losses beyond a specified Value at Risk (VaR) level. The key difference lies in their definitions and usage: ES commonly represents the expected loss given that the loss exceeds the VaR threshold, while CVaR often refers to the same concept but can also be defined as the weighted average of losses exceeding VaR or understood through optimization frameworks. ES is primarily used as a coherent risk measure satisfying subadditivity, whereas CVaR is widely applied in portfolio optimization due to its mathematical tractability and formulation as a convex function.
Calculation Methods for ES and CVaR
Expected Shortfall (ES) is calculated as the average loss exceeding the Value at Risk (VaR) at a specified confidence level, typically using historical simulation, variance-covariance, or Monte Carlo methods. Conditional Value at Risk (CVaR) often refers to the same risk measure as ES, emphasizing the tail expected loss beyond the VaR threshold, calculated similarly through averaging tail losses. Both metrics rely on integrating the tail distribution of losses, with CVaR frequently defined via optimization techniques in portfolio risk management.
Practical Applications in Portfolio Management
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) are interchangeable risk measures extensively applied in portfolio management to assess potential losses beyond the Value at Risk (VaR) threshold. Both ES and CVaR provide a coherent risk metric that captures tail risk, enabling portfolio managers to optimize asset allocation for downside protection under extreme market conditions. Practical applications include stress testing, optimizing portfolios to minimize tail risk, and regulatory capital allocation, enhancing risk-adjusted performance in diverse investment strategies.
Regulatory Perspective: Basel Accords and Risk Measures
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) are synonymous risk measures emphasized in Basel Accords for enhanced financial regulation, offering a coherent and tail-sensitive alternative to Value at Risk (VaR). Basel III mandates the integration of Expected Shortfall in market risk frameworks, particularly under the Fundamental Review of the Trading Book (FRTB), to capture extreme loss scenarios more accurately. Regulators prioritize ES for its subadditivity property and sensitivity to tail risk, promoting improved capital adequacy and systemic risk assessment in banking institutions.
Pros and Cons of ES and CVaR
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) both measure tail risk by assessing expected losses beyond a Value at Risk (VaR) threshold, with ES providing a coherent risk measure that addresses VaR's lack of subadditivity. ES offers advantages such as capturing extreme loss distributions and compatibility with regulatory frameworks like Basel III, but it can be computationally intensive and sensitive to model assumptions. CVaR, often used interchangeably with ES, serves as a risk metric convenient for optimization in portfolio management, yet may face challenges in interpretation and estimation accuracy under heavy-tailed asset return distributions.
Conclusion: Which Risk Measure Should You Use?
Expected Shortfall (ES) and Conditional Value at Risk (CVaR) both measure tail risk by assessing potential losses beyond a VaR threshold, but ES is widely recognized for its coherence and sensitivity to the shape of the loss distribution. CVaR provides a practical estimation of portfolio downside risk and is computationally efficient for optimization problems. Investors and risk managers should prefer Expected Shortfall when seeking a theoretically sound, coherent risk measure, while Conditional Value at Risk suits scenarios requiring straightforward calculation and implementation.
Expected Shortfall Infographic
 libterm.com
libterm.com