Exponential distribution models the time between events in a Poisson process, making it essential for reliability analysis and queuing theory. Its memoryless property means the probability of an event occurring in the future is independent of the past. Discover how understanding exponential distribution can enhance your data analysis by reading the full article.
Table of Comparison
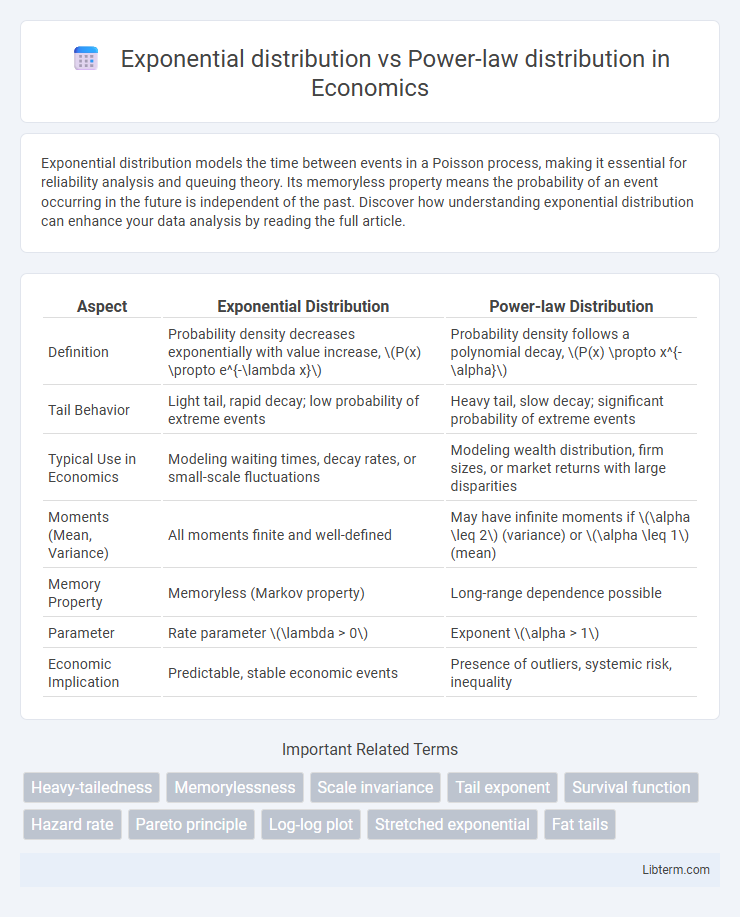
| Aspect | Exponential Distribution | Power-law Distribution |
|---|---|---|
| Definition | Probability density decreases exponentially with value increase, \(P(x) \propto e^{-\lambda x}\) | Probability density follows a polynomial decay, \(P(x) \propto x^{-\alpha}\) |
| Tail Behavior | Light tail, rapid decay; low probability of extreme events | Heavy tail, slow decay; significant probability of extreme events |
| Typical Use in Economics | Modeling waiting times, decay rates, or small-scale fluctuations | Modeling wealth distribution, firm sizes, or market returns with large disparities |
| Moments (Mean, Variance) | All moments finite and well-defined | May have infinite moments if \(\alpha \leq 2\) (variance) or \(\alpha \leq 1\) (mean) |
| Memory Property | Memoryless (Markov property) | Long-range dependence possible |
| Parameter | Rate parameter \(\lambda > 0\) | Exponent \(\alpha > 1\) |
| Economic Implication | Predictable, stable economic events | Presence of outliers, systemic risk, inequality |
Introduction to Exponential and Power-law Distributions
Exponential distribution models the time between events in a Poisson process, characterized by a constant hazard rate and an exponentially decreasing probability density function, making it ideal for describing memoryless processes. Power-law distribution exhibits a heavy tail where the probability of an event scales as a power of its size, often observed in natural and social phenomena with scale-invariance and large fluctuations. Understanding these distributions is crucial for modeling diverse data patterns, from failure rates and waiting times to wealth distribution and network connectivity.
Mathematical Definitions and Formulations
The Exponential distribution is defined by the probability density function \( f(x; \lambda) = \lambda e^{-\lambda x} \) for \( x \geq 0 \), where \( \lambda > 0 \) is the rate parameter, characterizing memoryless decay and constant failure rate. The Power-law distribution is expressed in its probability density function form as \( f(x; \alpha, x_{\min}) = \frac{\alpha - 1}{x_{\min}} \left(\frac{x}{x_{\min}}\right)^{-\alpha} \) for \( x \geq x_{\min} > 0 \), with scaling exponent \( \alpha > 1 \), indicating heavy-tailed probabilities and scale-invariance. Both formulations describe vastly different tail behaviors, with exponential distributions exhibiting rapid decay and power-law distributions showing polynomial decay, critical for modeling phenomena in various scientific fields.
Core Differences: Exponential vs Power-law
Exponential distribution features a constant hazard rate with probabilities that decay rapidly and predictably, making extreme events rare and less impactful. Power-law distribution exhibits heavy tails with probabilities that decay polynomially, allowing for frequent and significant extreme events that dominate the system's behavior. Unlike exponential decay, power-law distributions lack a characteristic scale, leading to scale-invariance and fractal-like structures in complex systems.
Real-world Applications and Examples
Exponential distributions model phenomena with a constant hazard rate, making them ideal for describing radioactive decay, waiting times in Poisson processes, and failure rates in reliability engineering. Power-law distributions capture heavy-tailed phenomena where large events occur with non-negligible probability, commonly observed in earthquake magnitudes, city population sizes, and wealth distribution in economics. These distinct distribution types guide risk assessment and decision-making in fields such as finance, natural disaster prediction, and network science.
Visualizing the Distributions: Plots and Patterns
Visualizing the exponential distribution reveals a rapidly decaying curve with a constant hazard rate, typically displayed as a smooth, downward-sloping exponential curve on log-linear plots. In contrast, power-law distribution visualizations show a straight line on log-log plots, indicating heavy tails and scale-invariance, highlighting the presence of extreme values with higher probabilities than exponential decay. These distinct plot patterns help differentiate memoryless processes from complex, self-similar phenomena across various scientific fields.
Statistical Properties and Behaviors
Exponential distributions exhibit a constant hazard rate with a rapid decay in tail probabilities, indicating events occur independently with a fixed rate parameter l, leading to memoryless behavior. Power-law distributions display heavy tails characterized by a polynomial decay function P(x) ~ x^(-a), often signifying scale-invariance and clustering behavior with higher probabilities for extreme values. Statistical properties of exponential distributions include finite mean and variance, whereas power-law distributions can have infinite variance or mean depending on the scaling exponent a, fundamentally affecting the modeling of phenomena like income inequality or natural disasters.
Common Misconceptions and Pitfalls
Exponential distribution is often mistaken for power-law distribution due to their heavy-tailed properties, but exponential decay is characterized by a constant hazard rate, while power-law exhibits scale invariance and a polynomial tail. A common pitfall is incorrectly fitting empirical data to an exponential model when the data follows a power-law, leading to significant underestimation of extreme events' probabilities. Misinterpreting the cutoff behavior in empirical distributions can cause confusion; exponential tails decay faster than power laws, which influences risk assessment and modeling in fields like finance and network theory.
Fitting Data to Exponential and Power-law Models
Fitting data to exponential and power-law models involves distinct statistical approaches tailored to their unique properties. Exponential distribution fitting often relies on maximum likelihood estimation (MLE) for its rate parameter l, which characterizes memoryless decay, while power-law fitting requires methods like MLE combined with goodness-of-fit tests such as the Kolmogorov-Smirnov statistic to estimate the scaling parameter a and determine the minimum cutoff value xmin. Accurate model fitting includes comparing log-likelihoods and employing likelihood ratio tests to discern whether data better follows an exponential or power-law tail, essential for applications in network theory, natural phenomena, and risk assessment.
Choosing the Right Distribution for Your Data
Exponential distribution suits datasets with a constant hazard rate and rapid decay in tail probabilities, ideal for modeling time between independent events like radioactive decay or Poisson processes. Power-law distribution effectively models data with heavy tails or scale-invariance, common in social networks, wealth distribution, and natural phenomena where large events have non-negligible probabilities. Selecting the right distribution involves analyzing the empirical data's tail behavior, assessing goodness-of-fit through methods like maximum likelihood estimation or Kolmogorov-Smirnov tests, and considering the underlying generative processes to ensure accurate representation and prediction.
Conclusion: Key Takeaways and Future Perspectives
Exponential distribution models decay processes with a characteristic scale, while power-law distribution captures scale-free, heavy-tailed phenomena often observed in natural and social systems. Key takeaways highlight exponential's suitability for well-defined events and power-law's relevance in complex networks and extreme event analysis. Future perspectives emphasize integrating hybrid models and advancing statistical methods for improved data fitting and prediction accuracy in diverse fields like physics, biology, and finance.
Exponential distribution Infographic
 libterm.com
libterm.com