Regression Discontinuity is a powerful statistical technique used to identify causal effects by exploiting a predetermined cutoff or threshold in observational data. This method helps you estimate treatment effects with higher validity when randomized experiments are not feasible. Explore the rest of the article to understand how Regression Discontinuity can enhance your data analysis approach.
Table of Comparison
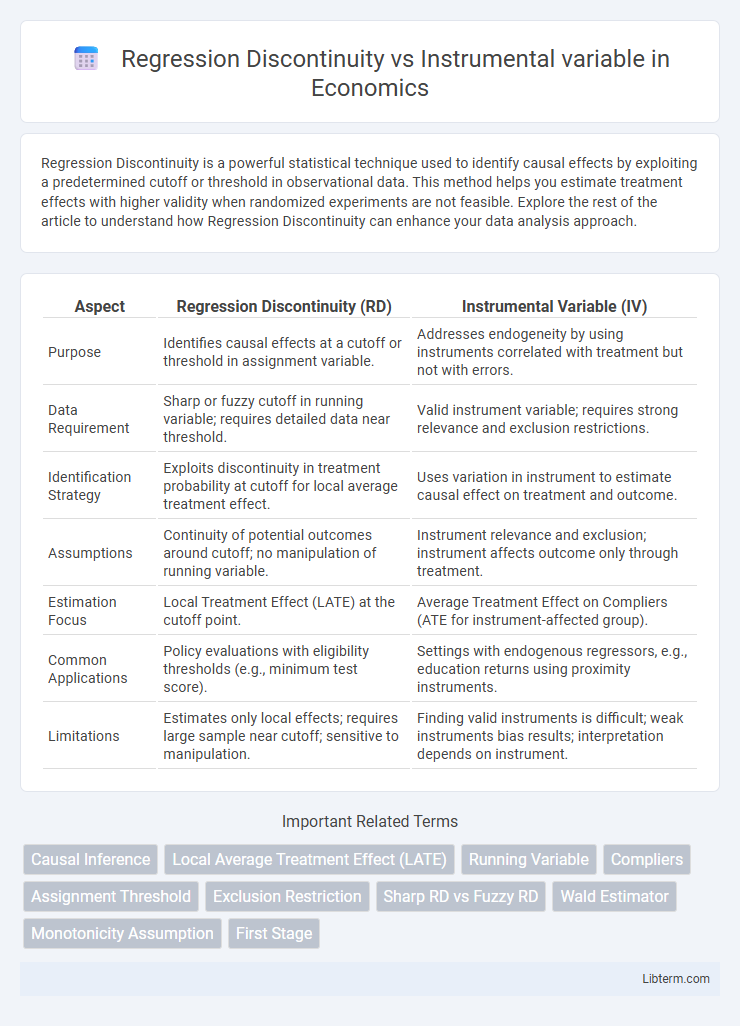
| Aspect | Regression Discontinuity (RD) | Instrumental Variable (IV) |
|---|---|---|
| Purpose | Identifies causal effects at a cutoff or threshold in assignment variable. | Addresses endogeneity by using instruments correlated with treatment but not with errors. |
| Data Requirement | Sharp or fuzzy cutoff in running variable; requires detailed data near threshold. | Valid instrument variable; requires strong relevance and exclusion restrictions. |
| Identification Strategy | Exploits discontinuity in treatment probability at cutoff for local average treatment effect. | Uses variation in instrument to estimate causal effect on treatment and outcome. |
| Assumptions | Continuity of potential outcomes around cutoff; no manipulation of running variable. | Instrument relevance and exclusion; instrument affects outcome only through treatment. |
| Estimation Focus | Local Treatment Effect (LATE) at the cutoff point. | Average Treatment Effect on Compliers (ATE for instrument-affected group). |
| Common Applications | Policy evaluations with eligibility thresholds (e.g., minimum test score). | Settings with endogenous regressors, e.g., education returns using proximity instruments. |
| Limitations | Estimates only local effects; requires large sample near cutoff; sensitive to manipulation. | Finding valid instruments is difficult; weak instruments bias results; interpretation depends on instrument. |
Understanding Regression Discontinuity and Instrumental Variables
Regression Discontinuity (RD) design exploits a predefined cutoff or threshold in an assignment variable to estimate causal effects, assuming units just above and below the cutoff are comparable, thereby mimicking randomized experiments. Instrumental Variables (IV) methods address endogeneity by using external variables, or instruments, that influence the treatment but do not directly affect the outcome except through the treatment. Both RD and IV techniques aim to identify causal relationships but rely on different assumptions: RD assumes a sharp or fuzzy cutoff, while IV depends on the validity and strength of the instrument.
Key Principles: Regression Discontinuity Design
Regression Discontinuity Design (RDD) leverages a predefined cutoff or threshold in an assignment variable to identify causal effects by comparing observations just above and below this boundary. The key principle involves exploiting this discontinuity to approximate a randomized experiment, ensuring that units near the cutoff are similar except for treatment status. This method relies on the assumption that no other factors systematically change at the threshold, enabling credible estimation of local treatment effects.
Key Principles: Instrumental Variable Approach
The Instrumental Variable (IV) approach relies on using an instrument that influences the treatment assignment but has no direct effect on the outcome except through the treatment, ensuring identification of causal effects in the presence of endogeneity. Key principles include relevance, where the instrument must be strongly correlated with the endogenous explanatory variable, and exclusion restriction, which requires the instrument to be independent of the error term in the outcome equation. IV estimation often addresses bias caused by omitted variables or measurement errors, providing consistent estimates when randomized experiments are infeasible.
Core Assumptions and Validity Criteria
Regression Discontinuity (RD) relies on a clearly defined cutoff or threshold to assign treatment, assuming individuals cannot precisely manipulate their assignment variable around this cutoff, ensuring local randomization. Instrumental Variable (IV) methods require a valid instrument that influences the treatment but affects the outcome only through that treatment, adhering to relevance, exclusion restriction, and independence assumptions. The validity of RD hinges on a continuous relationship of potential outcomes around the cutoff, while IV validity depends on the instrument's strength and the absence of direct paths to the outcome outside the treatment effect.
Causal Inference: Comparing Methodologies
Regression Discontinuity (RD) exploits a predefined cutoff to identify causal effects by comparing observations narrowly above and below the threshold, ensuring high internal validity with local treatment effects. Instrumental Variables (IV) address endogeneity by using external instruments correlated with the treatment but uncorrelated with the error term, enabling estimation of causal effects even in the presence of hidden confounders. Both RD and IV methodologies are pivotal in causal inference, with RD providing precise local average treatment effects and IV offering broader applicability when randomization is not feasible.
Strengths and Limitations of Regression Discontinuity
Regression Discontinuity (RD) offers a robust method for causal inference by exploiting a predetermined cutoff in assignment, providing clear identification with minimal reliance on instrumental variable assumptions. Its main strength lies in local validity near the threshold, reducing confounding biases when the cutoff is strictly enforced and the running variable is continuous. Limitations include reduced external validity beyond the cutoff region and sensitivity to bandwidth choices, making it less suitable for generalized treatment effect estimation compared to Instrumental Variable approaches.
Advantages and Challenges of Instrumental Variables
Instrumental variables (IV) offer a powerful method to address endogeneity by isolating exogenous variation correlated with the treatment but not directly with the outcome, enabling causal inference when randomized experiments are infeasible. A key advantage of IV lies in its applicability to settings where natural experiments or valid instruments exist, helping to overcome omitted variable bias and measurement errors. However, challenges include finding strong, valid instruments that satisfy relevance and exclusion restrictions, and the method's sensitivity to weak instrument bias which can lead to inconsistent estimators and unreliable inference.
Practical Applications in Empirical Research
Regression Discontinuity (RD) and Instrumental Variable (IV) methods are powerful tools for causal inference in empirical research, with RD excelling in settings where a clear cutoff or threshold determines treatment assignment, such as education policy evaluations or clinical trial eligibility. IV methods are more flexible, handling endogeneity in variables lacking sharp assignment rules by using external instruments, frequently applied in labor economics, health economics, and social sciences to address issues like measurement error or omitted variable bias. Both methods require strong assumptions--RD demands a well-defined cutoff and continuity of potential outcomes, while IV demands a valid instrument correlated with the endogenous regressor but uncorrelated with the error term--making their practical application context-dependent and crucial for credible identification.
Choosing the Right Method: Decision Factors
Choosing between Regression Discontinuity (RD) and Instrumental Variable (IV) methods hinges on the nature of the treatment assignment and data structure. RD is optimal when a clear cutoff or threshold determines treatment, ensuring local causal inference with strong internal validity, whereas IV is preferred for addressing endogeneity in continuous or non-threshold-based treatments through valid instruments. Key decision factors include the availability of a precise discontinuity, instrument relevance and exogeneity, sample size, and the specific causal estimand of interest.
Summary Table: Regression Discontinuity vs Instrumental Variables
Regression Discontinuity (RD) exploits a known cutoff or threshold in the assignment variable to identify causal effects locally around the discontinuity, ensuring high internal validity but limited generalizability beyond the cutoff region. Instrumental Variables (IV) use external instruments correlated with the endogenous explanatory variable but uncorrelated with the error term to identify causal effects, allowing broader applicability but relying heavily on instrument validity assumptions. The summary table highlights RD's precise local identification versus IV's wider, assumption-driven identification, emphasizing trade-offs between credibility and external validity in econometric analysis.
Regression Discontinuity Infographic
 libterm.com
libterm.com