The law of large numbers is a fundamental principle in probability stating that as the number of trials increases, the average of the results becomes closer to the expected value. This concept is crucial in fields like statistics, finance, and insurance for making reliable predictions from random events. Explore the full article to understand how the law of large numbers impacts your decision-making processes.
Table of Comparison
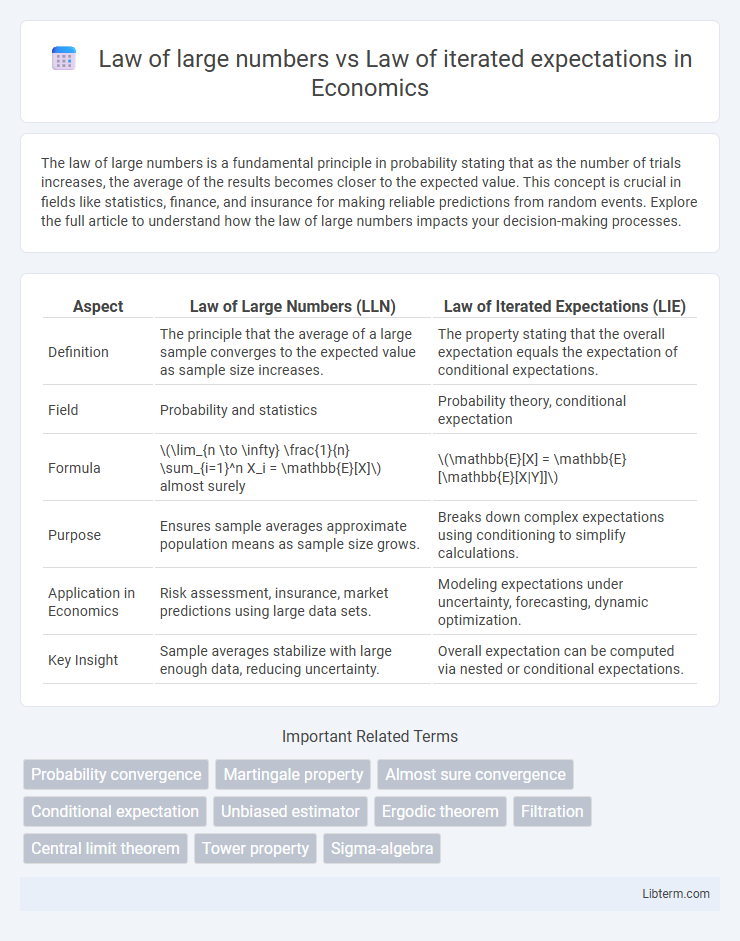
| Aspect | Law of Large Numbers (LLN) | Law of Iterated Expectations (LIE) |
|---|---|---|
| Definition | The principle that the average of a large sample converges to the expected value as sample size increases. | The property stating that the overall expectation equals the expectation of conditional expectations. |
| Field | Probability and statistics | Probability theory, conditional expectation |
| Formula | \(\lim_{n \to \infty} \frac{1}{n} \sum_{i=1}^n X_i = \mathbb{E}[X]\) almost surely | \(\mathbb{E}[X] = \mathbb{E}[\mathbb{E}[X|Y]]\) |
| Purpose | Ensures sample averages approximate population means as sample size grows. | Breaks down complex expectations using conditioning to simplify calculations. |
| Application in Economics | Risk assessment, insurance, market predictions using large data sets. | Modeling expectations under uncertainty, forecasting, dynamic optimization. |
| Key Insight | Sample averages stabilize with large enough data, reducing uncertainty. | Overall expectation can be computed via nested or conditional expectations. |
Introduction to Probability Theorems
The Law of Large Numbers states that as the number of independent, identically distributed random variables increases, their sample average converges to the expected value, ensuring long-term stability in probability. The Law of Iterated Expectations, also known as the Tower Property, expresses that the overall expectation of a random variable can be found by taking the expectation of its conditional expectation given another variable, effectively breaking down complex dependencies. Both theorems are fundamental in probability theory for analyzing expectations, providing tools to handle uncertainty and dependencies within stochastic processes.
Defining the Law of Large Numbers
The Law of Large Numbers (LLN) states that as the number of independent and identically distributed random variables increases, their sample average converges almost surely to the expected value or population mean. This principle underpins many statistical methods by ensuring long-term stability and predictability in averages computed from large datasets. Unlike the Law of Iterated Expectations, which concerns nested conditioning and the expectation of conditional expectations, the LLN focuses primarily on the convergence behavior of sample means to true expectations.
Understanding the Law of Iterated Expectations
The Law of Iterated Expectations states that the expected value of a conditional expectation equals the unconditional expectation, formalized as E[E(X|Y)] = E(X), ensuring consistency in hierarchical models. This principle is fundamental in econometrics and statistics for decomposing complex expectations when dealing with nested random variables or forecasting. Unlike the Law of Large Numbers, which concerns convergence of sample averages to the true mean with increasing sample size, the Law of Iterated Expectations provides a tool for managing expectations within conditioning frameworks.
Mathematical Formulations and Notations
The Law of Large Numbers (LLN) states that the sample average \( \bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i \) converges almost surely to the expected value \( \mathbb{E}[X] \) as \( n \to \infty \), emphasizing the stability of long-run averages. The Law of Iterated Expectations (LIE) is expressed as \( \mathbb{E}[X] = \mathbb{E}[\mathbb{E}[X \mid Y]] \), reflecting the tower property of conditional expectation where conditioning simplifies nested expectations. LLN focuses on convergence properties of empirical means with respect to probability measures, while LIE concerns the decomposition of expectations through conditional probabilities, both fundamental in probability theory and statistical inference.
Core Similarities: LLN vs LIE
The Law of Large Numbers (LLN) and the Law of Iterated Expectations (LIE) both underpin fundamental principles in probability theory related to the behavior of expectations and averages. LLN focuses on the convergence of sample averages to the expected value as the sample size increases, ensuring stability in empirical means. LIE, on the other hand, guarantees that the overall expected value equals the nested expectations taken iteratively over conditional distributions, highlighting the consistency of expectation computations in hierarchical or filtered information settings.
Key Differences in Assumptions and Applications
The Law of Large Numbers (LLN) assumes independent and identically distributed random variables, ensuring sample averages converge to the expected value, primarily applied in probability theory and statistics for estimating long-term frequencies. The Law of Iterated Expectations (LIE) relies on conditional expectations and sigma-algebras, emphasizing the nested structure of information, widely used in econometrics and decision theory to simplify complex expectations. LLN focuses on convergence properties of sample means, whereas LIE provides a foundational tool for decomposing expectations under varying information sets.
Practical Examples: LLN in Real-World Scenarios
The Law of Large Numbers (LLN) is observed in practical applications such as quality control, where the average defect rate stabilizes as the number of inspected items increases, ensuring reliable estimation of production quality. In finance, LLN explains how the average return of a diversified portfolio converges to the expected return over time, reducing the impact of random fluctuations. This contrasts with the Law of Iterated Expectations, which is primarily a theoretical tool used to evaluate nested conditional expectations rather than directly predicting long-run frequencies.
Use Cases for LIE in Economics and Statistics
The Law of Iterated Expectations (LIE) is essential in econometric modeling for breaking down complex conditional expectations into simpler, nested expectations, improving the analysis of dynamic economic processes. In statistics, LIE enables consistent estimation in hierarchical models by conditioning on intermediate sigma-algebras, facilitating unbiased predictions and variance decomposition. Applications in economics include policy evaluation through sequential decision-making models and predictive analysis of time series data, where LIE refines forecasts by incorporating additional information progressively.
Common Misconceptions and Clarifications
The Law of Large Numbers (LLN) states that the sample average converges to the expected value as the sample size increases, while the Law of Iterated Expectations (LIE) ensures that the expected value of a conditional expectation equals the unconditional expectation. A common misconception is that LLN implies convergence for any dependent observations, but it requires independence or weak dependence conditions, whereas LIE applies regardless of dependence structure in conditional expectations. Clarifying these distinctions prevents misapplication in statistical inference and reinforces the appropriate contexts for LLN's convergence and LIE's iterative averaging in probability theory.
Summary: Choosing the Right Law for Your Analysis
The Law of Large Numbers ensures that sample averages converge to the expected value as sample size increases, ideal for estimating population parameters from large datasets. The Law of Iterated Expectations breaks down complex expectations into nested conditional expectations, useful for sequential or hierarchical data structures. Selecting the right law depends on your analysis goal: use the Law of Large Numbers for long-run frequency interpretations and the Law of Iterated Expectations for conditional or multi-stage expectation modeling.
Law of large numbers Infographic
 libterm.com
libterm.com