The highest common factor (HCF) approach focuses on identifying the greatest number that divides two or more integers without leaving a remainder, optimizing problem-solving in mathematics. It simplifies fractions, improves number comparisons, and aids in algebraic expressions by efficiently reducing terms to their simplest forms. Explore the rest of the article to deepen your understanding of the HCF method and its practical applications.
Table of Comparison
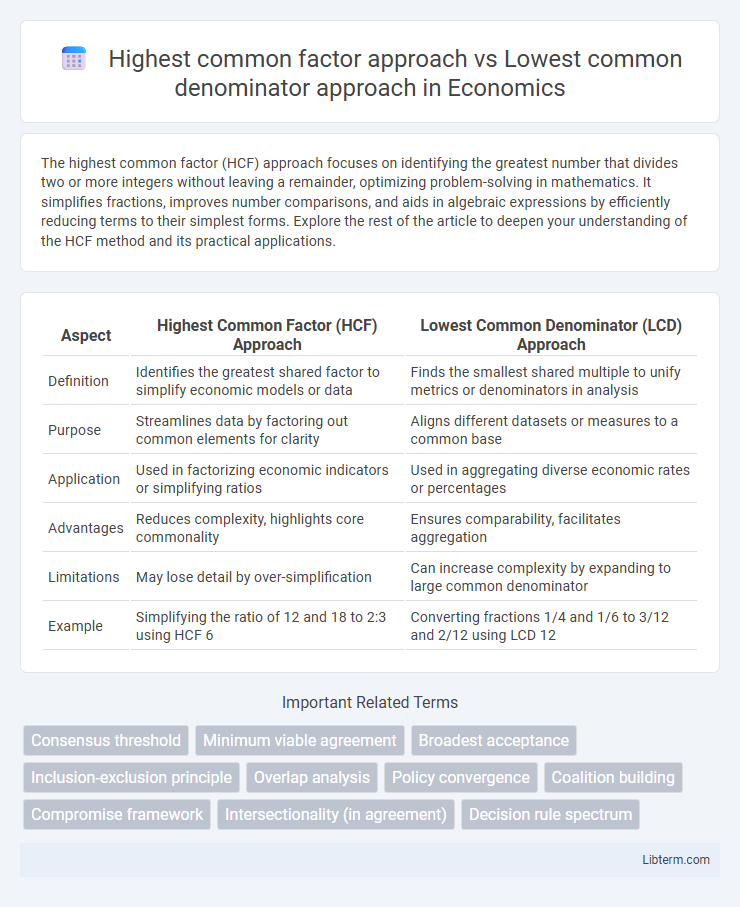
| Aspect | Highest Common Factor (HCF) Approach | Lowest Common Denominator (LCD) Approach |
|---|---|---|
| Definition | Identifies the greatest shared factor to simplify economic models or data | Finds the smallest shared multiple to unify metrics or denominators in analysis |
| Purpose | Streamlines data by factoring out common elements for clarity | Aligns different datasets or measures to a common base |
| Application | Used in factorizing economic indicators or simplifying ratios | Used in aggregating diverse economic rates or percentages |
| Advantages | Reduces complexity, highlights core commonality | Ensures comparability, facilitates aggregation |
| Limitations | May lose detail by over-simplification | Can increase complexity by expanding to large common denominator |
| Example | Simplifying the ratio of 12 and 18 to 2:3 using HCF 6 | Converting fractions 1/4 and 1/6 to 3/12 and 2/12 using LCD 12 |
Introduction to HCF and LCD Approaches
The Highest Common Factor (HCF) approach identifies the greatest integer that divides two or more numbers without leaving a remainder, optimizing problems involving divisibility and simplification. The Lowest Common Denominator (LCD) approach finds the smallest common multiple of denominators in fractions, facilitating efficient addition, subtraction, and comparison of fractional values. Both HCF and LCD are fundamental in number theory and arithmetic operations, enhancing computational accuracy and problem-solving efficiency.
Defining Highest Common Factor Approach
The Highest Common Factor (HCF) approach identifies the greatest divisor shared by two or more numbers, emphasizing commonalities to simplify fractions or solve problems involving divisibility. This method enhances efficiency in calculations by focusing on the maximum factor that evenly divides all given values. Utilizing HCF streamlines processes in number theory, algebra, and real-world applications requiring factorization or ratio simplification.
Understanding Lowest Common Denominator Approach
The Lowest Common Denominator (LCD) approach involves finding the smallest common multiple of denominators to simplify operations with fractions by converting them to equivalent fractions with the same denominator. This method streamlines addition, subtraction, and comparison of fractions, ensuring consistency and accuracy in calculations. Unlike the Highest Common Factor (HCF) approach that focuses on greatest common divisors to reduce fractions, the LCD approach prioritizes a common base for seamless fraction alignment.
Core Principles of Each Method
The Highest Common Factor (HCF) approach focuses on identifying the greatest common divisor shared by two or more numbers, emphasizing factorization to simplify expressions or solve problems efficiently. The Lowest Common Denominator (LCD) approach centers on finding the smallest common multiple of denominators in fractions, enabling uniformity for addition, subtraction, or comparison tasks. Both methods rely on prime factorization and multiples, but HCF targets maximization of divisors while LCD prioritizes minimization of shared multiples.
Application in Mathematical Problem Solving
The Highest Common Factor (HCF) approach simplifies problems involving divisibility and factorization by identifying the largest number that divides two or more integers without a remainder, facilitating solutions in fraction reduction and algebraic expressions. The Lowest Common Denominator (LCD) approach is critical for adding, subtracting, or comparing fractions by finding the smallest common multiple of denominators, ensuring uniformity in fractional operations. Both methods optimize mathematical problem-solving efficiency by addressing different aspects of number relationships: HCF for commonality in factors and LCD for harmonizing denominators.
Benefits of Using HCF Approach
The Highest Common Factor (HCF) approach simplifies fractions more efficiently by reducing them to their smallest equivalent form, ensuring minimal numerators and denominators. This method enhances accuracy in mathematical operations such as addition, subtraction, and comparison by preventing unnecessary complexity in calculations. Using HCF also improves problem-solving speed and facilitates easier interpretation of results in various practical applications like ratio analysis and simplifying algebraic expressions.
Advantages of LCD Approach
The Lowest Common Denominator (LCD) approach simplifies the addition and subtraction of fractions by converting them to a common base, minimizing complexity in calculations. This method reduces the risk of errors compared to the Highest Common Factor (HCF) approach, which often involves more intricate factorization and comparison steps. LCD ensures uniformity in denominator handling, making it especially beneficial in educational settings and computational algorithms.
Limitations and Challenges of Both Methods
The Highest Common Factor (HCF) approach often struggles with scalability issues when dealing with large numbers or complex fractions, limiting its efficiency in computational applications. The Lowest Common Denominator (LCD) method faces challenges in processing time and memory usage, particularly when denominators have multiple prime factors leading to large least common multiples. Both methods can encounter difficulties in handling irrational or algebraic expressions, reducing their applicability in advanced mathematical and engineering problems.
Choosing the Right Approach: Factors to Consider
Choosing the right approach between the Highest Common Factor (HCF) and Lowest Common Denominator (LCD) depends on the mathematical context and the problem's requirements. HCF is ideal for simplifying fractions by dividing both numerator and denominator by their greatest shared factor, enhancing fraction reduction efficiency. LCD is preferred when adding or subtracting fractions with different denominators, as it finds a common multiple to align denominators for accurate calculation.
Conclusion: HCF vs LCD Approach
The Highest Common Factor (HCF) approach simplifies problems by focusing on factors that divide numbers evenly, making it ideal for reducing fractions and finding commonalities efficiently. The Lowest Common Denominator (LCD) approach, however, is essential for adding or subtracting fractions as it identifies a common base for comparison. Choosing between HCF and LCD depends on the mathematical operation, with HCF optimizing simplification tasks and LCD facilitating combination processes.
Highest common factor approach Infographic
 libterm.com
libterm.com