Covered Interest Parity (CIP) ensures that the difference in interest rates between two countries is offset by the forward exchange rate, eliminating arbitrage opportunities in the foreign exchange market. This fundamental principle guarantees that investors cannot make riskless profits by exploiting discrepancies in interest rates and currency values. Discover how understanding CIP can enhance your strategies in international finance by exploring the full article.
Table of Comparison
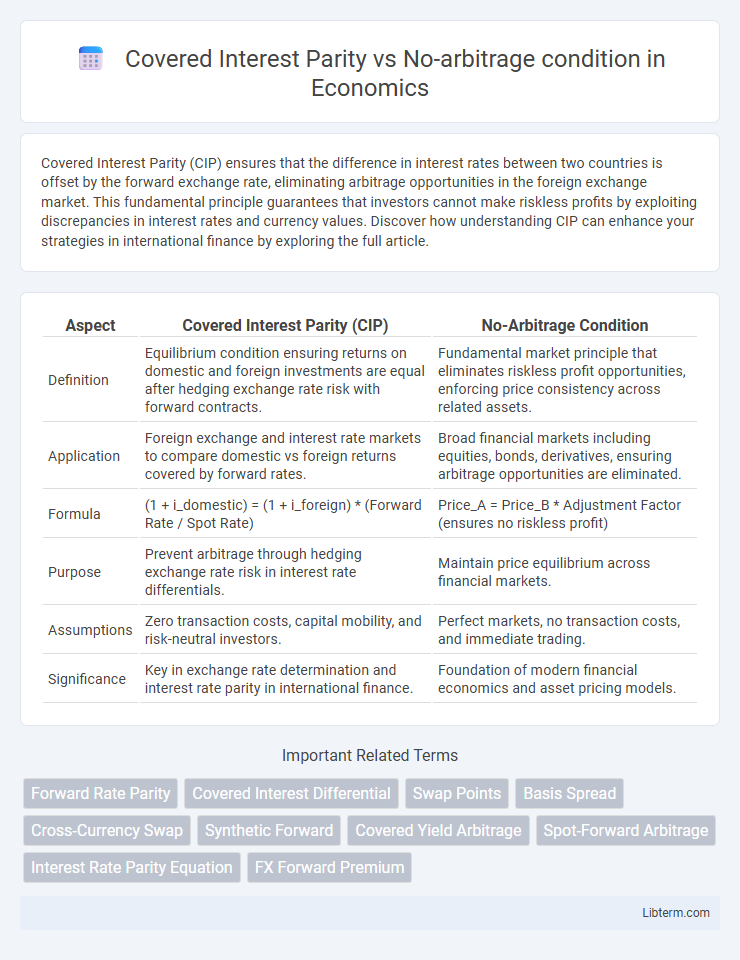
| Aspect | Covered Interest Parity (CIP) | No-Arbitrage Condition |
|---|---|---|
| Definition | Equilibrium condition ensuring returns on domestic and foreign investments are equal after hedging exchange rate risk with forward contracts. | Fundamental market principle that eliminates riskless profit opportunities, enforcing price consistency across related assets. |
| Application | Foreign exchange and interest rate markets to compare domestic vs foreign returns covered by forward rates. | Broad financial markets including equities, bonds, derivatives, ensuring arbitrage opportunities are eliminated. |
| Formula | (1 + i_domestic) = (1 + i_foreign) * (Forward Rate / Spot Rate) | Price_A = Price_B * Adjustment Factor (ensures no riskless profit) |
| Purpose | Prevent arbitrage through hedging exchange rate risk in interest rate differentials. | Maintain price equilibrium across financial markets. |
| Assumptions | Zero transaction costs, capital mobility, and risk-neutral investors. | Perfect markets, no transaction costs, and immediate trading. |
| Significance | Key in exchange rate determination and interest rate parity in international finance. | Foundation of modern financial economics and asset pricing models. |
Introduction to Covered Interest Parity (CIP)
Covered Interest Parity (CIP) is a fundamental principle in international finance that ensures the returns on domestic and foreign investments are equalized when hedged for exchange rate risk using forward contracts. It states that the interest rate differential between two countries is equal to the differential between the forward and spot exchange rates, eliminating arbitrage opportunities. CIP maintains equilibrium in foreign exchange and interest rate markets by tightly linking interest rates, spot currency prices, and forward exchange rates.
Defining the No-arbitrage Condition
The no-arbitrage condition in international finance ensures that there are no opportunities to earn riskless profits from discrepancies in interest rates and exchange rates between two countries. It requires the forward exchange rate to adjust so that the returns on domestic and foreign assets, when hedged against exchange rate risk, are equalized. Covered Interest Parity (CIP) is a direct application of this condition, linking spot and forward exchange rates with interest rate differentials to prevent arbitrage in currency markets.
Core Concepts of Covered Interest Parity
Covered Interest Parity (CIP) ensures that the return on domestic and foreign investments, when hedged for exchange rate risk via forward contracts, is equalized to prevent arbitrage opportunities. The core principle involves the relationship between spot exchange rates, forward exchange rates, and interest rates of two countries, such that the forward premium or discount offsets interest rate differentials. This no-arbitrage condition stipulates that any deviation from CIP would allow riskless profits through simultaneous borrowing and lending in different currencies, enforcing equilibrium in the foreign exchange and interest rate markets.
The Mechanics Behind No-arbitrage
The mechanics behind the no-arbitrage condition in covered interest parity (CIP) ensure that the forward exchange rates adjust to eliminate riskless profit opportunities from discrepancies between interest rates and spot exchange rates. Arbitrageurs exploit any deviation by simultaneously borrowing in a low-interest currency, converting at the spot rate, investing in a high-interest currency, and locking in the forward rate to cover future currency risk. This process enforces equality among spot rates, forward rates, and interest rate differentials, maintaining equilibrium in global foreign exchange and money markets.
Mathematical Representation of CIP and No-arbitrage
Covered Interest Parity (CIP) is mathematically represented as \( (1 + i_d) = \frac{F}{S}(1 + i_f) \), where \(i_d\) and \(i_f\) are domestic and foreign interest rates, \(F\) is the forward exchange rate, and \(S\) is the spot exchange rate, ensuring no arbitrage profits in currency markets. The no-arbitrage condition states that the return on domestic investment must equal the hedged return on foreign investment, encapsulated by the equation \( (1 + i_d) = \frac{F}{S}(1 + i_f) \), which guarantees equilibrium in international financial markets. Both CIP and the no-arbitrage principle rely on equality in returns adjusted for forward exchange contracts, preventing riskless profit opportunities through covered currency trades.
Real-world Applications of Covered Interest Parity
Covered Interest Parity (CIP) ensures that the returns on hedged foreign investments are aligned across countries, eliminating arbitrage opportunities in efficient markets. Real-world applications of CIP include managing currency risk in multinational corporations, guiding central banks in setting interest rates, and informing investors on pricing forward exchange contracts. Empirical studies show minor deviations from CIP during financial crises, highlighting its role in understanding market stress and currency market stability.
Factors Influencing No-arbitrage in Financial Markets
Factors influencing no-arbitrage in financial markets include interest rate differentials, exchange rate expectations, and transaction costs, all essential for maintaining Covered Interest Parity (CIP). Market liquidity and regulatory frameworks also play critical roles by affecting capital flows and pricing efficiency. Deviations from CIP often signal arbitrage opportunities until adjustments in these factors restore equilibrium.
Key Differences: CIP vs No-arbitrage
Covered Interest Parity (CIP) specifically relates to the equilibrium condition linking spot and forward exchange rates with interest rates in two countries, ensuring no arbitrage opportunities in currency markets through covered interest rate arbitrage. The no-arbitrage condition is a broader financial principle stating that asset prices must prevent riskless profit opportunities across all markets, including but not limited to FX and derivatives. Unlike the general no-arbitrage framework, CIP applies exclusively to foreign exchange markets and involves forward contracts, making it a specific application within the no-arbitrage paradigm.
Empirical Evidence and Case Studies
Empirical evidence on Covered Interest Parity (CIP) frequently reveals deviations, especially during financial crises, challenging the no-arbitrage condition that assumes perfect market equilibrium. Case studies from the 2008 global financial crisis and post-COVID-19 market disruptions illustrate persistent CIP violations due to factors like regulatory constraints, liquidity shortages, and credit risk premiums. These findings underscore that while the no-arbitrage condition remains a foundational principle for arbitrage-free pricing, real-world frictions often cause CIP deviations, impacting currency forward markets and hedging strategies.
Conclusion: Implications for Investors and Policymakers
Covered Interest Parity (CIP) ensures that arbitrage opportunities are eliminated in foreign exchange markets by linking spot and forward exchange rates with interest rate differentials, solidifying no-arbitrage conditions. For investors, adherence to CIP implies that returns on hedged foreign investments are predictable and risk-adjusted, reducing exposure to exchange rate fluctuations. Policymakers rely on CIP as a benchmark to maintain market efficiency and stability, with deviations signaling potential market distortions or regulatory interventions needed to restore equilibrium.
Covered Interest Parity Infographic
 libterm.com
libterm.com