The Laffer Curve illustrates the relationship between tax rates and tax revenue, showing that beyond a certain point, higher tax rates can lead to decreased revenue due to reduced economic activity. Understanding this concept helps policymakers balance taxation and growth to optimize fiscal outcomes. Explore the rest of the article to see how the Laffer Curve impacts your economy and tax planning.
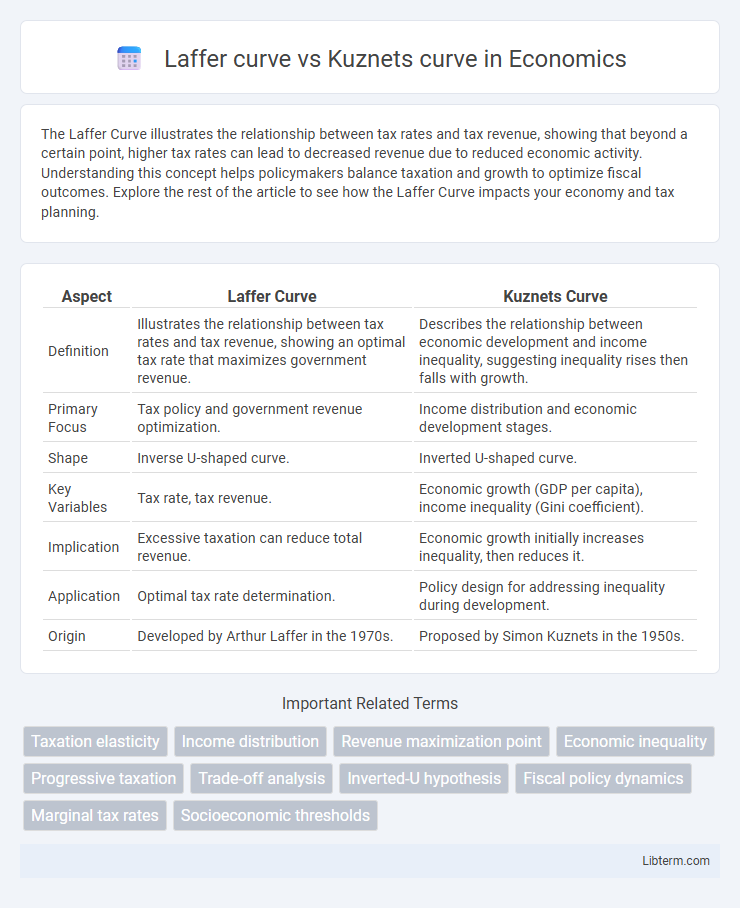
Table of Comparison
| Aspect | Laffer Curve | Kuznets Curve |
|---|---|---|
| Definition | Illustrates the relationship between tax rates and tax revenue, showing an optimal tax rate that maximizes government revenue. | Describes the relationship between economic development and income inequality, suggesting inequality rises then falls with growth. |
| Primary Focus | Tax policy and government revenue optimization. | Income distribution and economic development stages. |
| Shape | Inverse U-shaped curve. | Inverted U-shaped curve. |
| Key Variables | Tax rate, tax revenue. | Economic growth (GDP per capita), income inequality (Gini coefficient). |
| Implication | Excessive taxation can reduce total revenue. | Economic growth initially increases inequality, then reduces it. |
| Application | Optimal tax rate determination. | Policy design for addressing inequality during development. |
| Origin | Developed by Arthur Laffer in the 1970s. | Proposed by Simon Kuznets in the 1950s. |
Introduction to the Laffer Curve and Kuznets Curve
The Laffer Curve illustrates the relationship between tax rates and tax revenue, demonstrating that increasing tax rates beyond a certain point can reduce total revenue by discouraging economic activity. The Kuznets Curve depicts the trend between income inequality and economic development, showing that inequality tends to increase during early stages of growth and decrease after reaching a certain income level. Both curves offer critical insights into fiscal policy and economic inequality dynamics, shaping debates on taxation and social welfare.
Historical Background of Each Curve
The Laffer Curve, developed in the 1970s by economist Arthur Laffer, illustrates the relationship between tax rates and tax revenue, emphasizing how increasing tax rates beyond a certain point can decrease government revenue. The Kuznets Curve, introduced by economist Simon Kuznets in the 1950s, depicts the relationship between economic inequality and economic development, suggesting that inequality initially rises and then declines during the industrialization process. Both curves emerged from empirical observations during periods of significant economic policy and structural change in the United States.
Fundamental Concepts: Taxation vs. Economic Inequality
The Laffer Curve illustrates the relationship between tax rates and tax revenue, suggesting that there is an optimal tax rate that maximizes revenue without discouraging productivity. The Kuznets Curve hypothesizes an inverted U-shaped relationship between economic inequality and economic development, where inequality rises during early industrialization and decreases as a society becomes wealthier. While the Laffer Curve focuses on taxation efficiency and incentives, the Kuznets Curve addresses the dynamics of income distribution throughout economic growth stages.
Mathematical Representation: Laffer Curve
The Laffer Curve is mathematically represented as a parabolic function describing the relationship between tax rates and tax revenue, typically expressed as R = t(1 - t) where R is revenue and t is the tax rate. This quadratic function peaks at an optimal tax rate that maximizes revenue before decreasing as tax rates further increase, illustrating the diminishing returns of taxation. The curve highlights the economic principle that excessively high tax rates can lead to reduced incentives to work or invest, thus lowering overall tax revenue.
Mathematical Representation: Kuznets Curve
The Kuznets Curve is mathematically represented as an inverted U-shaped quadratic function depicting the relationship between income inequality and economic development, often expressed as \( I = \alpha + \beta Y + \gamma Y^2 + \epsilon \), where \( I \) is income inequality, \( Y \) denotes per capita income, and coefficients \( \beta > 0 \), \( \gamma < 0 \) capture the initial rise and subsequent decline in inequality. This functional form models how inequality first increases during early stages of economic growth before decreasing after reaching a certain income threshold. The quadratic nature of the Kuznets Curve contrasts with the Laffer Curve's tax revenue function, emphasizing nonlinear dynamics in socio-economic variables.
Key Assumptions and Criticisms
The Laffer Curve assumes a relationship between tax rates and government revenue, positing that beyond a certain tax rate, higher taxes discourage work and investment, reducing revenue, but it is criticized for oversimplifying economic behavior and lacking empirical precision in optimal tax rates. The Kuznets Curve assumes an inverse U-shaped relation between income inequality and economic development, where inequality rises in early growth stages and falls as economies mature, yet critics argue it overlooks institutional factors and varying country trajectories. Both curves rely on simplified models that abstract complex social dynamics, leading to debates over their universal applicability and policy relevance.
Policy Implications: Fiscal Policy vs. Social Policy
The Laffer curve illustrates the optimal tax rate that maximizes government revenue without discouraging productivity, guiding fiscal policy toward balancing taxation and economic growth. In contrast, the Kuznets curve emphasizes the relationship between economic development and income inequality, shaping social policy to address inequality through targeted redistribution and welfare programs. Policymakers use the Laffer curve to design efficient tax systems, while the Kuznets curve informs strategies for social equity and sustainable development.
Real-World Applications and Empirical Evidence
The Laffer Curve demonstrates the relationship between tax rates and tax revenue, with real-world applications seen in countries adjusting tax policies to optimize revenue without discouraging productivity, supported by empirical studies in the United States and Europe showing revenue declines beyond certain tax thresholds. The Kuznets Curve illustrates the inverse-U relationship between economic growth and income inequality, applied in policymaking to balance development and social equity, with empirical evidence from developing economies revealing inequality rises in early growth stages before declining as wealth distribution improves. Both curves inform fiscal and economic policies, guiding governments in taxation strategies and inequality management based on observed data trends and economic theory validations.
Comparative Analysis: Similarities and Differences
The Laffer Curve and Kuznets Curve both illustrate relationships between economic variables using a graphical representation that highlights trade-offs and optimal points. The Laffer Curve models the relationship between tax rates and tax revenue, showing how beyond a certain tax rate, revenue declines due to decreased economic activity, while the Kuznets Curve depicts income inequality relative to economic development, indicating inequality rises then falls with GDP growth. Key differences include the Laffer Curve's focus on fiscal policy and taxation efficiency versus the Kuznets Curve's emphasis on social inequality dynamics during economic transitions.
Conclusion: Lessons for Economic Policy
The Laffer curve illustrates the relationship between tax rates and tax revenue, emphasizing the balance needed to optimize fiscal policy without discouraging economic activity. The Kuznets curve highlights how income inequality initially worsens during economic development before improving, guiding policies toward inclusive growth. Policymakers must carefully calibrate tax strategies to foster growth while addressing inequality through targeted social and economic reforms.
Laffer curve Infographic
 libterm.com
libterm.com