The Efficient Market Hypothesis (EMH) asserts that financial markets are informationally efficient, meaning asset prices fully reflect all available information at any given time. This theory challenges the possibility of consistently outperforming the market through stock picking or market timing since price changes are essentially unpredictable. Explore this article to understand how EMH impacts investing strategies and market behavior.
Table of Comparison
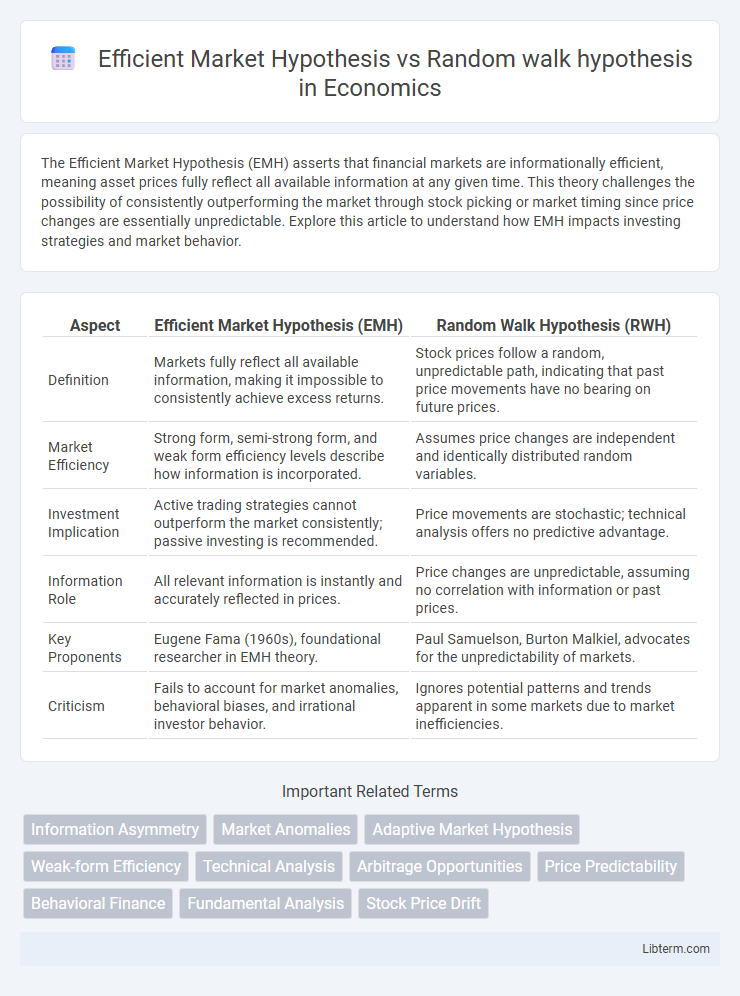
| Aspect | Efficient Market Hypothesis (EMH) | Random Walk Hypothesis (RWH) |
|---|---|---|
| Definition | Markets fully reflect all available information, making it impossible to consistently achieve excess returns. | Stock prices follow a random, unpredictable path, indicating that past price movements have no bearing on future prices. |
| Market Efficiency | Strong form, semi-strong form, and weak form efficiency levels describe how information is incorporated. | Assumes price changes are independent and identically distributed random variables. |
| Investment Implication | Active trading strategies cannot outperform the market consistently; passive investing is recommended. | Price movements are stochastic; technical analysis offers no predictive advantage. |
| Information Role | All relevant information is instantly and accurately reflected in prices. | Price changes are unpredictable, assuming no correlation with information or past prices. |
| Key Proponents | Eugene Fama (1960s), foundational researcher in EMH theory. | Paul Samuelson, Burton Malkiel, advocates for the unpredictability of markets. |
| Criticism | Fails to account for market anomalies, behavioral biases, and irrational investor behavior. | Ignores potential patterns and trends apparent in some markets due to market inefficiencies. |
Introduction to Market Theories
Efficient Market Hypothesis (EMH) asserts that asset prices fully reflect all available information, making it impossible to consistently achieve higher returns than the overall market. The Random Walk Hypothesis suggests that stock price changes are independent of each other and follow a random path, implying that past price movements cannot predict future prices. Both theories underpin fundamental market theories, shaping the understanding of price behavior and investment strategies in financial economics.
Defining the Efficient Market Hypothesis
The Efficient Market Hypothesis (EMH) posits that financial markets are informationally efficient, meaning asset prices fully reflect all available information at any given time. Under EMH, it is impossible to consistently achieve higher returns than the overall market through stock picking or market timing, as new information is quickly and accurately incorporated into prices. This contrasts with the Random Walk Hypothesis, which suggests that stock price changes are independent and unpredictable, emphasizing the inherent randomness in market movements.
Understanding the Random Walk Hypothesis
The Random Walk Hypothesis posits that stock price changes are independent and identically distributed, making future prices unpredictable based on past data. This theory implies that markets are inherently efficient in reflecting all available information, aligning closely with the Efficient Market Hypothesis (EMH) but emphasizing price randomness. Empirical studies support the random walk model by showing that price movements exhibit no discernible patterns, challenging investors' ability to consistently outperform the market through technical analysis.
Key Assumptions of Both Hypotheses
The Efficient Market Hypothesis (EMH) assumes that all available information is fully and instantaneously reflected in asset prices, implying investors cannot consistently achieve abnormal returns. The Random Walk Hypothesis posits that stock price changes are independent and identically distributed, making future price movements unpredictable and devoid of any pattern. Both hypotheses emphasize market unpredictability but differ on the role of information processing and market participant behavior in price formation.
Historical Background and Development
The Efficient Market Hypothesis (EMH), introduced by Eugene Fama in the 1960s, posits that asset prices fully reflect all available information, making consistent outperformance impossible. The Random Walk Hypothesis, stemming from earlier works by Maurice Kendall and later popularized by Burton Malkiel's 1973 book "A Random Walk Down Wall Street," suggests that stock price changes are independent and random, resembling a random walk. Both theories emerged from efforts to explain and model the unpredictability of financial markets, shaping modern financial economics and investment strategies.
Empirical Evidence Supporting Each Hypothesis
Empirical evidence for the Efficient Market Hypothesis (EMH) includes numerous studies showing that stock prices reflect all available information, making it impossible to consistently achieve abnormal returns through stock picking or market timing. Conversely, research supporting the Random Walk Hypothesis finds that stock price changes are statistically independent and follow a random pattern, reinforcing the idea that future price movements cannot be predicted from past trends. Both hypotheses rely on extensive analysis of market data, with EMH supported by event studies on information dissemination and Random Walk backed by statistical tests on price time series.
Differences Between EMH and Random Walk Theory
The Efficient Market Hypothesis (EMH) asserts that all available information is instantly reflected in stock prices, implying that predicting future price movements is impossible, whereas the Random Walk Hypothesis suggests that stock prices follow a completely unpredictable path, making past price patterns irrelevant. EMH categorizes market efficiency into weak, semi-strong, and strong forms, emphasizing varying degrees of information accessibility, while Random Walk Theory primarily focuses on the statistical randomness of price changes without categorizing market efficiency. Unlike EMH, Random Walk Theory does not explicitly account for the role of information or investor behavior in price formation, but rather assumes price changes are independent and identically distributed random variables.
Criticisms and Limitations of Both Models
The Efficient Market Hypothesis (EMH) faces criticism for assuming all information is instantly reflected in stock prices, overlooking market anomalies and investor irrationality. The Random Walk Hypothesis is challenged for ignoring predictable patterns and behavioral biases that can influence price movements. Both models are limited by their reliance on idealized assumptions, which fail to capture market complexities and the impact of psychological factors on asset pricing.
Implications for Investors and Portfolio Management
The Efficient Market Hypothesis (EMH) asserts that stock prices fully reflect all available information, implying that investors cannot consistently achieve alpha through stock selection or market timing, which supports passive portfolio management strategies like index investing. In contrast, the Random Walk Hypothesis suggests that price changes are unpredictable and independent, reinforcing the difficulty of forecasting market movements and endorsing diversification to manage risk rather than attempting to outperform the market. Both hypotheses emphasize market efficiency, guiding investors toward low-cost, broadly diversified portfolios to optimize risk-adjusted returns over the long term.
Conclusion: Evaluating Market Predictability
The Efficient Market Hypothesis (EMH) asserts that asset prices reflect all available information, making consistent market prediction impossible, while the Random Walk Hypothesis suggests price changes are independent and unpredictable. Both theories emphasize the difficulty of outperforming the market through forecasting, highlighting inherent market unpredictability. Empirical studies often support EMH's notion of informational efficiency, reinforcing the challenge of achieving abnormal returns through predictive models.
Efficient Market Hypothesis Infographic
 libterm.com
libterm.com