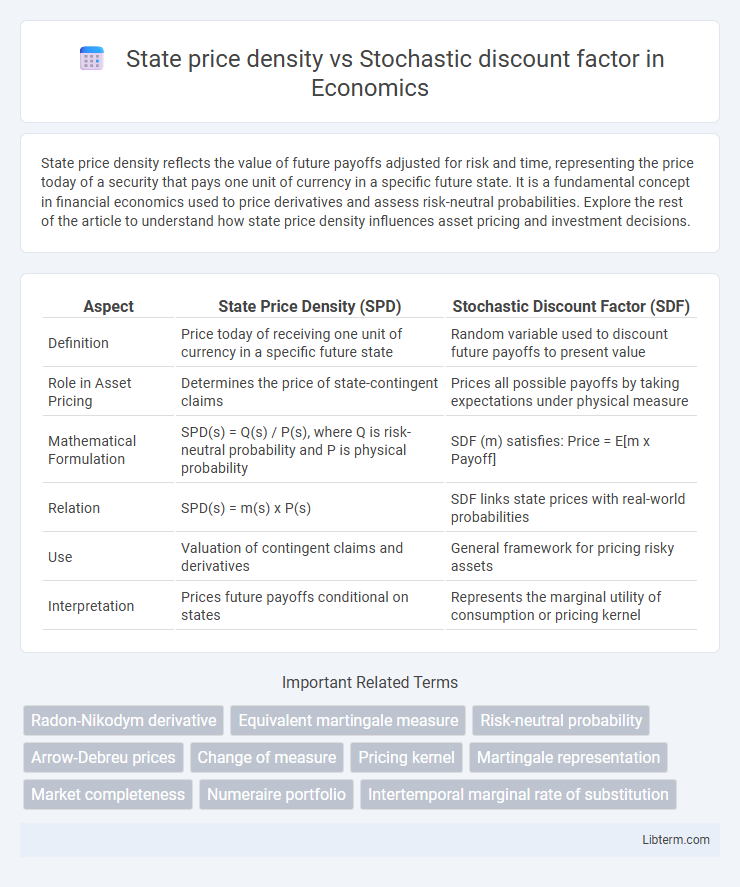
State price density reflects the value of future payoffs adjusted for risk and time, representing the price today of a security that pays one unit of currency in a specific future state. It is a fundamental concept in financial economics used to price derivatives and assess risk-neutral probabilities. Explore the rest of the article to understand how state price density influences asset pricing and investment decisions.
Table of Comparison
| Aspect | State Price Density (SPD) | Stochastic Discount Factor (SDF) |
|---|---|---|
| Definition | Price today of receiving one unit of currency in a specific future state | Random variable used to discount future payoffs to present value |
| Role in Asset Pricing | Determines the price of state-contingent claims | Prices all possible payoffs by taking expectations under physical measure |
| Mathematical Formulation | SPD(s) = Q(s) / P(s), where Q is risk-neutral probability and P is physical probability | SDF (m) satisfies: Price = E[m x Payoff] |
| Relation | SPD(s) = m(s) x P(s) | SDF links state prices with real-world probabilities |
| Use | Valuation of contingent claims and derivatives | General framework for pricing risky assets |
| Interpretation | Prices future payoffs conditional on states | Represents the marginal utility of consumption or pricing kernel |
Introduction to State Price Density and Stochastic Discount Factor
State price density represents the present value of a payoff in a specific future state, reflecting the price of a state-contingent claim in financial markets. The stochastic discount factor, also known as the pricing kernel, is a random variable used to discount future cash flows to their present value, capturing both time value and risk preferences. Both concepts are fundamental for asset pricing, linking probabilities and payoffs to market prices via risk-adjusted expectations.
Core Definitions and Mathematical Framework
State price density (SPD) represents the price today of a unit payoff contingent on a specific future state, mathematically defined as the Radon-Nikodym derivative of the equivalent martingale measure with respect to the physical probability measure. The stochastic discount factor (SDF), also known as the pricing kernel or marginal rate of substitution, discounts future payoffs to present value, linking asset prices to expected discounted payoffs under the real-world measure. Both concepts satisfy the fundamental pricing equation \( P_t = \mathbb{E}^P[M_{t+1} X_{t+1} | \mathcal{F}_t] \), where \( P_t \) is asset price, \( M_{t+1} \) the SDF, and \( X_{t+1} \) the payoff, with SPD functioning as the state-specific pricing weight derived from the SDF's decomposition.
Economic Intuition Behind State Price Density
State price density represents the price today of receiving one unit of currency in a specific future state, reflecting investor preferences and probabilities assigned to uncertain outcomes. It serves as a fundamental building block in pricing contingent claims by connecting probabilities with discounting, essentially weighting future payoffs according to their economic desirability. Unlike the stochastic discount factor, which is a random variable applied multiplicatively to payoffs, state price density directly encodes the value of each possible state, providing clearer intuition into how risk and time affect asset pricing.
Understanding the Stochastic Discount Factor (SDF)
The Stochastic Discount Factor (SDF) is a fundamental concept in asset pricing that captures the state-price density, reflecting the present value of a payoff contingent on future states of the world. Unlike deterministic discount factors, the SDF varies with uncertainty and encapsulates both time preference and risk aversion, enabling the pricing of assets in incomplete markets. Understanding the SDF facilitates insights into risk-neutral probabilities and the valuation of contingent claims by linking marginal utility growth to market prices.
Relationships Between State Price Density and SDF
State price density (SPD) represents the present value of a payoff in a particular state of the world, reflecting the price of a state-contingent claim. The stochastic discount factor (SDF), also known as the pricing kernel, discounts future payoffs by weighting them according to their marginal utility across states, establishing an intrinsic connection to SPD. Mathematically, the SPD equals the product of the risk-free discount factor and the SDF, making the SDF a key driver in determining state price densities and hence asset prices.
Role in Asset Pricing Models
State price density represents the price today of a security that pays one unit of currency if a particular state of the world occurs in the future, serving as a key input in derivative pricing and risk-neutral valuation. The stochastic discount factor (SDF) adjusts future payoffs for time value and risk, discounting them to present value while capturing investors' marginal utility of consumption across different states. Both concepts are fundamental in asset pricing models, where state price density helps identify risk-neutral probabilities, and the stochastic discount factor ensures equilibrium pricing by linking asset returns to agents' preferences and market risk.
Empirical Estimation Techniques for Each Concept
State price density estimation relies on nonparametric and kernel-based methods to extract risk-neutral probabilities from option prices and asset returns, highlighting market-implied information. Stochastic discount factor (SDF) estimation typically employs generalized method of moments (GMM) and Euler equation-based techniques, leveraging time-series data on consumption and asset returns to identify intertemporal marginal rates of substitution. Both approaches require careful calibration to address measurement errors and ensure consistency with observed market dynamics.
Applications in Financial Derivatives and Risk Management
State price density, also known as the Arrow-Debreu price, reflects the price today of a security paying off in a specific future state and serves as a fundamental tool for pricing financial derivatives by enabling the construction of risk-neutral probability measures. The stochastic discount factor (SDF) generalizes this concept by incorporating time and uncertainty preferences, allowing for dynamic pricing and comprehensive risk adjustments in derivatives valuation. Both tools are essential in risk management, where state price densities provide insights into the state-contingent payoffs while the SDF facilitates asset pricing under diverse stochastic processes, enhancing hedging strategies and risk assessment models.
Common Misconceptions and Pitfalls
State price density and stochastic discount factor are often confused, but they differ fundamentally: state price density represents the price today of a security paying off in a particular state tomorrow, whereas the stochastic discount factor (SDF) adjusts future payoffs to present value, reflecting risk preferences. A common misconception is treating state price density as an SDF, ignoring that the SDF normalizes by the real-world probability measure, which affects pricing and risk assessment. Misinterpreting these concepts can lead to incorrect asset pricing, improper hedging strategies, and flawed risk management models due to misaligned theoretical foundations.
Key Takeaways and Future Research Directions
State price density and stochastic discount factor are fundamental concepts in financial economics that facilitate asset pricing by linking payoffs to present values under uncertainty. Both represent equivalent pricing kernels but differ in interpretation: state price density quantifies the price of a unit payoff in each state of the world, while the stochastic discount factor adjusts payoffs for time value and risk preferences. Future research aims to refine estimation techniques under complex market dynamics, explore their roles in incomplete markets, and enhance empirical validation using high-frequency and big data methodologies.
State price density Infographic
 libterm.com
libterm.com