Shear modulus measures a material's ability to resist deformation under shear stress, reflecting its rigidity and elastic behavior. Understanding this property helps engineers design structures and materials that withstand forces without permanent distortion. Explore the rest of the article to learn how shear modulus impacts various applications in engineering and materials science.
Table of Comparison
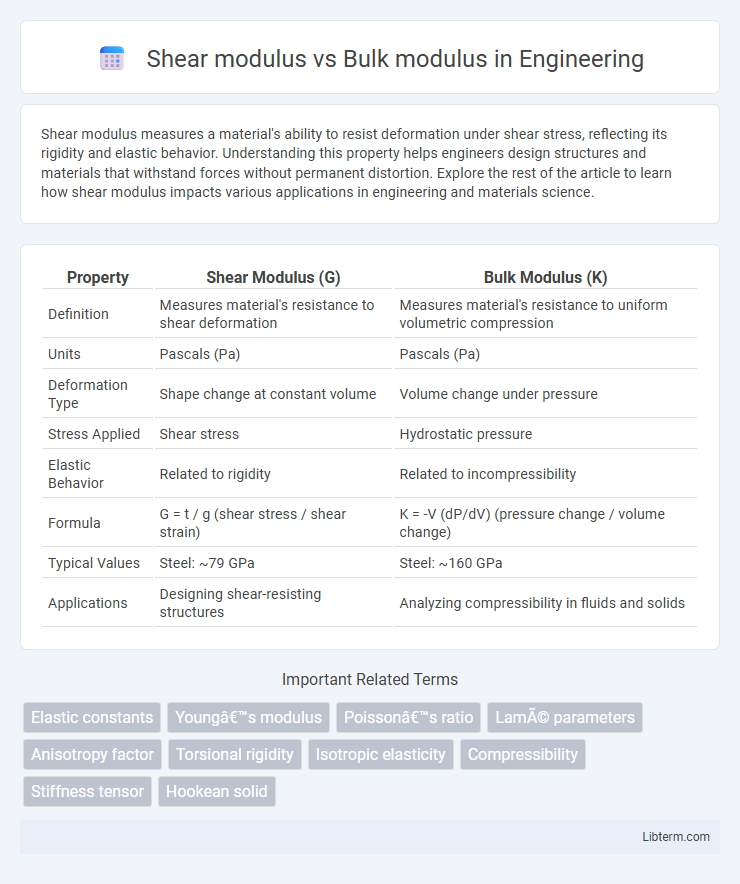
| Property | Shear Modulus (G) | Bulk Modulus (K) |
|---|---|---|
| Definition | Measures material's resistance to shear deformation | Measures material's resistance to uniform volumetric compression |
| Units | Pascals (Pa) | Pascals (Pa) |
| Deformation Type | Shape change at constant volume | Volume change under pressure |
| Stress Applied | Shear stress | Hydrostatic pressure |
| Elastic Behavior | Related to rigidity | Related to incompressibility |
| Formula | G = t / g (shear stress / shear strain) | K = -V (dP/dV) (pressure change / volume change) |
| Typical Values | Steel: ~79 GPa | Steel: ~160 GPa |
| Applications | Designing shear-resisting structures | Analyzing compressibility in fluids and solids |
Introduction to Shear Modulus and Bulk Modulus
Shear modulus measures a material's resistance to shape changes under shear stress, reflecting its rigidity and ability to withstand angular deformation. Bulk modulus quantifies a material's resistance to uniform compression, indicating its incompressibility under pressure. Both moduli are fundamental mechanical properties used to characterize elastic behavior in solids and influence material selection in engineering applications.
Fundamental Definitions
Shear modulus measures a material's resistance to shape changes under applied shear stress, reflecting its rigidity and deformation behavior in response to tangential forces. Bulk modulus quantifies a material's resistance to uniform compression, indicating how incompressible the material is when subjected to pressure in all directions. Both moduli serve as fundamental elastic constants essential for characterizing mechanical properties and predicting material response under different loading conditions.
Mathematical Formulations
Shear modulus (G) quantifies a material's response to shear stress and is mathematically defined as G = t/g, where t is the shear stress and g is the shear strain. Bulk modulus (K) measures a material's resistance to uniform compression, expressed by K = -V(P/V), indicating the ratio of volumetric stress to volumetric strain. Both moduli are intrinsic elastic constants that relate to Young's modulus (E) and Poisson's ratio (n) through the equations G = E/[2(1 + n)] and K = E/[3(1 - 2n)].
Key Differences Between Shear and Bulk Modulus
Shear modulus measures a material's resistance to shape changes under shear stress, while bulk modulus quantifies its resistance to uniform compression or volumetric changes. Shear modulus is crucial for understanding elasticity in materials subjected to forces parallel to their surfaces, whereas bulk modulus is vital for applications involving pressure and volume changes such as fluid mechanics and geophysics. The units for both moduli are pascals (Pa), but their physical implications differ, with shear modulus relating to rigidity and bulk modulus relating to incompressibility.
Physical Interpretation and Units
Shear modulus measures a material's resistance to shape changes under shear stress, quantified in pascals (Pa), reflecting elasticity in deformation without volume change. Bulk modulus quantifies a material's resistance to uniform compression, also in pascals (Pa), indicating the material's incompressibility by relating pressure change to volume change. Both moduli are fundamental in characterizing mechanical properties, with shear modulus relating to rigidity and bulk modulus to compressibility.
Role in Material Science
Shear modulus measures a material's resistance to shape changes under shear stress, crucial for understanding elasticity and deformation in solids. Bulk modulus quantifies a material's resistance to uniform compression, essential for analyzing volumetric changes under pressure. Both moduli help material scientists predict mechanical behavior, design resilient materials, and tailor properties for applications like structural engineering and aerospace.
Measurement Methods
Shear modulus is measured using torsional or transverse wave methods, which analyze an object's response to shear stress through oscillatory or deformation tests. Bulk modulus is determined by applying uniform pressure to a material and measuring the resulting volumetric strain using techniques such as ultrasonic pulse velocity tests or hydrostatic compression experiments. Both moduli require precise instrumentation to capture stress-strain relationships, enabling characterization of elastic properties under different loading conditions.
Applications in Engineering and Industry
Shear modulus and bulk modulus play critical roles in engineering and industrial applications by describing material behavior under different types of stress; shear modulus measures resistance to shape changes under shear stress, essential for designing beams, shafts, and gears, while bulk modulus quantifies resistance to uniform compression, vital for hydraulic systems, pressure vessels, and fluid mechanics. Materials with high shear modulus are preferred in structural components subjected to torsion or shear forces, ensuring stability and durability. High bulk modulus materials are crucial in applications requiring minimal volume change under pressure, such as in deep-sea exploration equipment and gas storage tanks.
Factors Affecting Shear and Bulk Moduli
Shear modulus and bulk modulus are influenced by factors such as the material's atomic bonding strength, temperature, and microstructural defects. Increased temperature generally decreases both moduli by weakening atomic interactions, while impurities and dislocations reduce shear modulus more significantly due to their impact on shape deformation resistance. The bulk modulus is mainly affected by the material's compressibility and density, with higher density materials typically exhibiting larger bulk moduli.
Summary and Comparative Analysis
Shear modulus measures a material's resistance to shape changes under shear stress, whereas bulk modulus quantifies resistance to uniform compression. Materials with high shear modulus exhibit rigidity against shape deformation, while those with high bulk modulus resist volumetric changes under pressure. Comparative analysis reveals that metals often have higher bulk moduli relative to their shear moduli, indicating stronger volume compression resistance compared to shape deformation.
Shear modulus Infographic
 libterm.com
libterm.com