The Brayton cycle describes the thermodynamic process underpinning gas turbine engines, involving compression, combustion, and expansion stages to convert fuel into mechanical energy efficiently. Its operation is fundamental in power plants and aircraft engines, where optimizing performance and fuel consumption are critical. Explore the full article to understand how your energy systems benefit from the Brayton cycle.
Table of Comparison
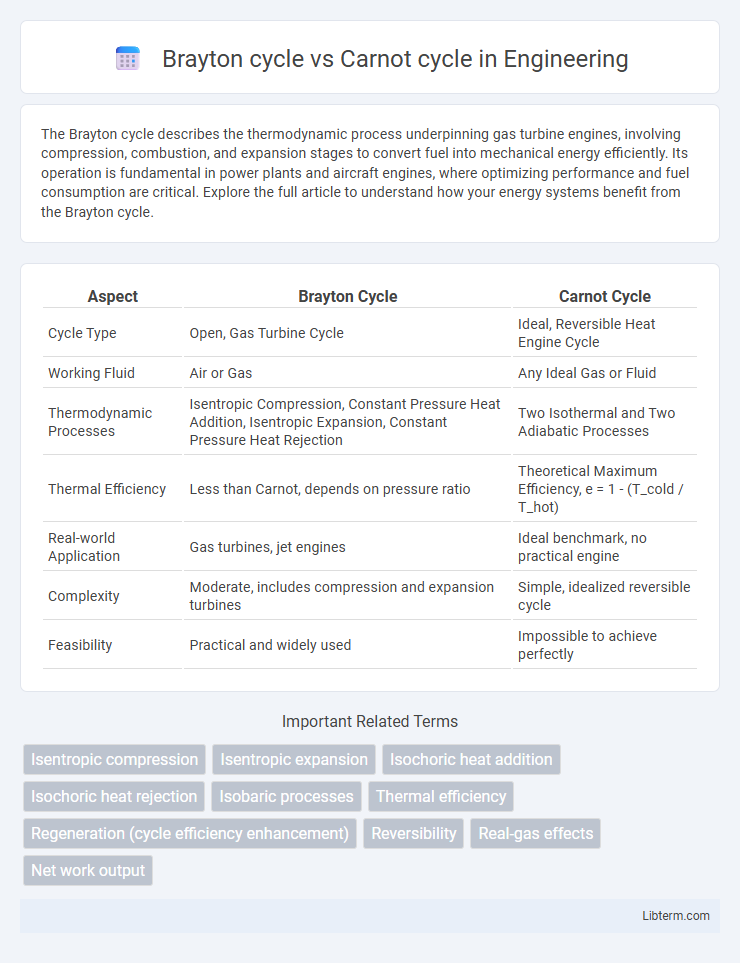
| Aspect | Brayton Cycle | Carnot Cycle |
|---|---|---|
| Cycle Type | Open, Gas Turbine Cycle | Ideal, Reversible Heat Engine Cycle |
| Working Fluid | Air or Gas | Any Ideal Gas or Fluid |
| Thermodynamic Processes | Isentropic Compression, Constant Pressure Heat Addition, Isentropic Expansion, Constant Pressure Heat Rejection | Two Isothermal and Two Adiabatic Processes |
| Thermal Efficiency | Less than Carnot, depends on pressure ratio | Theoretical Maximum Efficiency, e = 1 - (T_cold / T_hot) |
| Real-world Application | Gas turbines, jet engines | Ideal benchmark, no practical engine |
| Complexity | Moderate, includes compression and expansion turbines | Simple, idealized reversible cycle |
| Feasibility | Practical and widely used | Impossible to achieve perfectly |
Introduction to Brayton and Carnot Cycles
The Brayton cycle, commonly used in gas turbine engines, operates on a constant pressure heat addition process, making it ideal for jet propulsion and power generation. The Carnot cycle represents an idealized engine model with maximum thermal efficiency, functioning between two temperature reservoirs through reversible isothermal and adiabatic processes. Understanding the fundamental thermodynamic principles of both cycles highlights the practical efficiency and real-world application of Brayton cycles compared to the theoretical limits defined by the Carnot cycle.
Fundamental Principles of the Brayton Cycle
The Brayton cycle operates on the principle of constant-pressure heat addition and rejection, using a gas turbine unit that includes a compressor, combustion chamber, and turbine. Unlike the Carnot cycle, which is an idealized model based on reversible processes and maximum efficiency, the Brayton cycle reflects practical gas turbine engine operations with real fluid dynamics. The key components in the Brayton cycle work by compressing air, adding heat at constant pressure, and expanding the high-temperature gas to produce mechanical work.
Overview of the Carnot Cycle
The Carnot cycle is a theoretical thermodynamic cycle that defines the maximum possible efficiency achievable by a heat engine operating between two temperature reservoirs. It consists of two isothermal processes, where heat transfer occurs at constant temperature, and two adiabatic processes, where no heat exchange happens, ensuring reversible operation. This idealized cycle serves as a standard for evaluating real engine performance, contrasting with the Brayton cycle, which models practical gas turbine engines operating on continuous combustion and compression-expansion processes.
Key Components in Each Cycle
The Brayton cycle features key components such as a compressor, combustion chamber, and turbine, which facilitate continuous energy conversion from pressurized air and fuel. The Carnot cycle, idealized for maximum efficiency, consists of two isothermal processes and two adiabatic processes involving heat addition, heat rejection, compression, and expansion without specific mechanical parts. Understanding these components highlights the Brayton cycle's practical application in gas turbines and the Carnot cycle's role as a theoretical efficiency benchmark.
Thermodynamic Processes Compared
The Brayton cycle, used in gas turbine engines, operates on isentropic compression and expansion with constant-pressure heat addition and rejection, contrasting the Carnot cycle's isothermal heat transfer processes. The Carnot cycle, idealized for maximum efficiency, involves reversible isothermal and isentropic processes but is impractical for real engines due to its slow heat exchange requirements. The differences in thermodynamic processes directly impact the efficiency and feasibility of power cycles, with Brayton cycles favored in applied engineering due to their continuous flow and realistic operational conditions.
Efficiency: Brayton Cycle vs Carnot Cycle
The Brayton cycle, commonly used in jet engines and gas turbines, typically achieves lower thermal efficiency compared to the Carnot cycle due to inherent irreversibilities like friction and non-ideal gas behavior. While the Carnot cycle represents the theoretical maximum efficiency based on temperature limits, the Brayton cycle's efficiency depends on pressure ratio and turbine inlet temperature. Optimizing the Brayton cycle involves increasing pressure ratio and turbine inlet temperature, yet it remains less efficient than the idealized Carnot cycle operating between the same temperature limits.
Real-world Applications and Limitations
The Brayton cycle is widely used in jet engines and gas turbine power plants due to its ability to operate continuously and handle high power outputs efficiently. The Carnot cycle, while ideal for illustrating maximum thermodynamic efficiency, is impractical in real-world applications because it requires reversible processes and infinitely slow operation, making it unsuitable for power generation or propulsion. The Brayton cycle's real-world limitations include lower efficiency than the Carnot cycle and sensitivity to component losses, but its applicability in mechanical systems outweighs these constraints.
Impact on Power Generation Systems
The Brayton cycle, commonly used in gas turbine power plants, offers higher real-world efficiency due to continuous combustion and practical operating conditions compared to the idealized Carnot cycle. The Carnot cycle represents the maximum theoretical efficiency between two temperature reservoirs but is impractical for implementation in power generation systems because of its reversible and quasi-static processes. Power generation efficiency improvements rely on optimizing the Brayton cycle's pressure ratios and turbine inlet temperatures, making it more suitable for modern applications than the Carnot cycle.
Practical Considerations in Engineering
The Brayton cycle, commonly used in gas turbine engines, offers higher power output and efficiency at practical operating pressures and temperatures compared to the idealized Carnot cycle. Engineers prefer the Brayton cycle due to its compatibility with real-world components, such as compressors and turbines, and its ease of integration into combined cycle power plants. While the Carnot cycle establishes the theoretical maximum efficiency limit, it is impractical to implement because it requires reversible processes and infinite-time heat transfer, which are unattainable in engineering applications.
Future Trends and Developments
The future of Brayton cycle technology lies in enhancing efficiency through advanced materials and hybridization with renewable energy sources like solar and hydrogen. Innovations in high-temperature gas turbines and carbon capture integration are driving sustainable power generation trends. Carnot cycle developments primarily influence theoretical efficiency limits, guiding improvements in real-world thermodynamic cycles and next-generation heat engine designs.
Brayton cycle Infographic
 libterm.com
libterm.com