The Blasius correlation provides a simple empirical formula to estimate the friction factor for turbulent flow in smooth pipes, valid primarily for Reynolds numbers between 4,000 and 100,000. This relation, expressed as f = 0.316/Re^0.25, is widely used in engineering calculations to predict pressure drops and optimize fluid transport systems. Discover how the Blasius correlation can enhance your understanding of flow resistance by exploring the detailed applications and limitations outlined in the rest of this article.
Table of Comparison
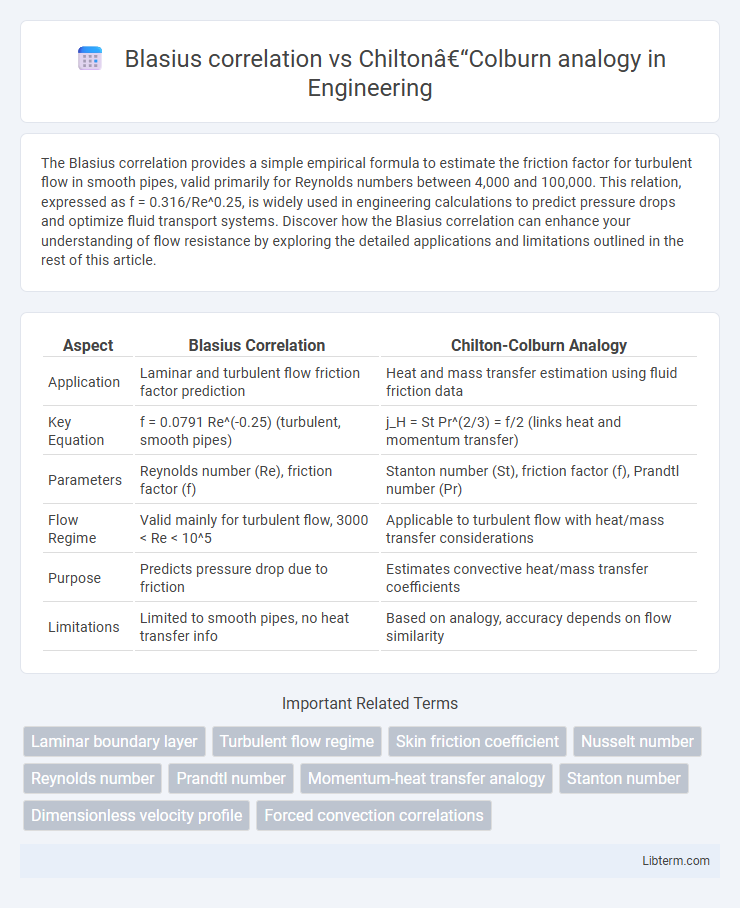
| Aspect | Blasius Correlation | Chilton-Colburn Analogy |
|---|---|---|
| Application | Laminar and turbulent flow friction factor prediction | Heat and mass transfer estimation using fluid friction data |
| Key Equation | f = 0.0791 Re^(-0.25) (turbulent, smooth pipes) | j_H = St Pr^(2/3) = f/2 (links heat and momentum transfer) |
| Parameters | Reynolds number (Re), friction factor (f) | Stanton number (St), friction factor (f), Prandtl number (Pr) |
| Flow Regime | Valid mainly for turbulent flow, 3000 < Re < 10^5 | Applicable to turbulent flow with heat/mass transfer considerations |
| Purpose | Predicts pressure drop due to friction | Estimates convective heat/mass transfer coefficients |
| Limitations | Limited to smooth pipes, no heat transfer info | Based on analogy, accuracy depends on flow similarity |
Introduction to Blasius Correlation and Chilton–Colburn Analogy
Blasius correlation provides an empirical formula to estimate the friction factor in turbulent flow within smooth pipes, primarily applicable for Reynolds numbers between 4,000 and 100,000. Chilton-Colburn analogy extends the relationship between momentum, heat, and mass transfer by correlating heat transfer coefficients to friction factors, facilitating the calculation of convective heat transfer in turbulent flows. Both models serve as foundational tools in fluid dynamics and heat transfer engineering for predicting flow behavior and thermal performance.
Historical Background and Development
The Blasius correlation, formulated in 1913, was one of the earliest empirical formulas describing turbulent flow friction factors in smooth pipes, derived from experimental observations by Paul Richard Heinrich Blasius. In contrast, the Chilton-Colburn analogy, developed in the mid-20th century by Chilton and Colburn, extended heat and mass transfer analogies by relating momentum, heat, and mass transfer coefficients through dimensionless parameters like the Stanton number and friction factor. Both contributions have significantly shaped turbulent flow and heat transfer modeling, with Blasius focusing on fluid friction and Chilton-Colburn providing a unifying framework for transfer phenomena.
Fundamental Concepts in Fluid Mechanics and Heat/Mass Transfer
Blasius correlation describes the relationship between the friction factor and Reynolds number for laminar flow in smooth pipes, providing a fundamental basis for predicting pressure drop due to friction in fluid mechanics. Chilton-Colburn analogy extends this concept by linking momentum transfer to heat and mass transfer through dimensionless groups like the Colburn j-factor, enabling simultaneous analysis of convective heat and mass transfer phenomena. Both approaches underscore the use of dimensionless parameters to model transport processes, with Blasius focusing on hydrodynamic behavior and Chilton-Colburn bridging fluid flow with thermal and concentration boundary layers.
Blasius Correlation: Definition, Formula, and Applicability
The Blasius correlation is an empirical formula used to estimate the friction factor for laminar and turbulent flow in smooth pipes, expressed as \( f = 0.079 \, \text{Re}^{-0.25} \) for Reynolds numbers between 4000 and 10^5. It is particularly applicable to turbulent flow in smooth circular pipes and provides a simpler alternative to more complex relations when surface roughness is negligible. Compared to the Chilton-Colburn analogy, which relates heat, mass, and momentum transfer coefficients through dimensionless numbers, the Blasius correlation specifically targets fluid friction without incorporating mass or heat transfer effects.
Chilton–Colburn Analogy: Definition, Formula, and Significance
The Chilton-Colburn analogy establishes a relationship between heat, mass, and momentum transfer, expressed by the formula \( j_H = j_D = j_M \), where \( j_H \) is the heat transfer Stanton number, \( j_D \) the mass transfer Stanton number, and \( j_M \) the friction factor divided by two. This analogy is significant in engineering for predicting heat and mass transfer coefficients from known fluid flow data, particularly in turbulent flow conditions. It surpasses the Blasius correlation by incorporating mass and heat transfer together, allowing more comprehensive analysis in convective heat and mass transfer applications.
Assumptions and Limitations of Each Approach
The Blasius correlation assumes turbulent flow in smooth pipes and is limited to Reynolds numbers between 4,000 and 100,000, neglecting entrance effects and surface roughness. The Chilton-Colburn analogy extends to heat, mass, and momentum transfer by relating friction factor with heat and mass transfer coefficients, but assumes similar boundary layer behavior and constant physical properties, limiting its accuracy in highly variable or complex flow conditions. Both approaches are less reliable in transitional flow regimes and flows with significant pressure gradients or variable fluid properties.
Comparative Analysis: Blasius Correlation vs Chilton–Colburn Analogy
Blasius correlation is primarily used for predicting friction factors in turbulent flow within smooth pipes, relying on empirical data for the Reynolds number range from 3000 to 100,000. Chilton-Colburn analogy extends the analysis to simultaneous momentum, heat, and mass transfer, linking dimensionless numbers such as the Stanton number, friction factor, and Colburn j-factor across various flow conditions. Comparative analysis reveals that while Blasius correlation provides straightforward friction factor estimation, Chilton-Colburn analogy offers a more comprehensive framework for engineering applications involving combined transfer phenomena.
Practical Applications in Engineering Systems
Blasius correlation is commonly applied to estimate friction factors in turbulent pipe flows with smooth surfaces, aiding in the design of efficient piping and duct systems. Chilton-Colburn analogy extends this by linking momentum, heat, and mass transfer, enabling engineers to predict heat exchanger performance and optimize thermal system designs. Both models support system efficiency improvements but Chilton-Colburn offers broader applicability across various transfer phenomena in chemical and mechanical engineering processes.
Accuracy and Relevance in Modern Engineering Calculations
The Blasius correlation provides a simple empirical formula for estimating friction factors in turbulent pipe flow, offering reasonable accuracy for smooth pipes and moderate Reynolds numbers but limited applicability in complex or rough pipe conditions. The Chilton-Colburn analogy extends beyond friction factors by linking heat, mass, and momentum transfer, delivering enhanced relevance in modern multiphysics engineering problems where simultaneous calculation of heat and mass transfer coefficients is essential. Engineers prioritize the Chilton-Colburn analogy for its versatility and better alignment with experimental data in convective heat transfer, while the Blasius correlation remains useful for quick, approximate friction estimations in streamlined flow scenarios.
Conclusion: Selection Criteria and Future Perspectives
Blasius correlation offers a robust empirical formula for predicting friction factors in turbulent pipe flow, primarily effective in smooth, fully developed conditions, while the Chilton-Colburn analogy extends heat and mass transfer predictions by correlating them with momentum transfer, applicable in more diverse flow regimes. Selection between these models depends on flow characteristics, surface roughness, and required accuracy for heat or mass transfer analysis in engineering applications. Future perspectives emphasize integrating machine learning with classical correlations to enhance predictive accuracy and extending analogies to complex, multiphase flow systems.
Blasius correlation Infographic
 libterm.com
libterm.com