Damped oscillation occurs when an oscillating system loses energy over time, causing its amplitude to gradually decrease until motion eventually stops. This behavior is common in mechanical, electrical, and other physical systems where friction or resistance dissipates energy. Explore this article further to understand how damping affects oscillations and practical applications of this phenomenon in your everyday life.
Table of Comparison
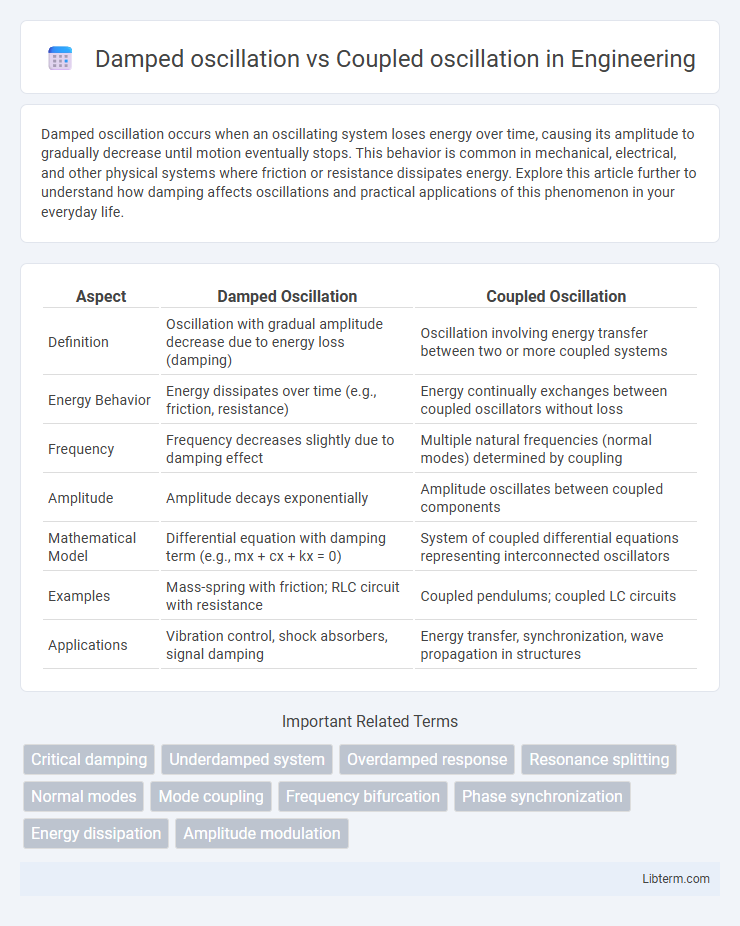
| Aspect | Damped Oscillation | Coupled Oscillation |
|---|---|---|
| Definition | Oscillation with gradual amplitude decrease due to energy loss (damping) | Oscillation involving energy transfer between two or more coupled systems |
| Energy Behavior | Energy dissipates over time (e.g., friction, resistance) | Energy continually exchanges between coupled oscillators without loss |
| Frequency | Frequency decreases slightly due to damping effect | Multiple natural frequencies (normal modes) determined by coupling |
| Amplitude | Amplitude decays exponentially | Amplitude oscillates between coupled components |
| Mathematical Model | Differential equation with damping term (e.g., mx + cx + kx = 0) | System of coupled differential equations representing interconnected oscillators |
| Examples | Mass-spring with friction; RLC circuit with resistance | Coupled pendulums; coupled LC circuits |
| Applications | Vibration control, shock absorbers, signal damping | Energy transfer, synchronization, wave propagation in structures |
Introduction to Damped and Coupled Oscillations
Damped oscillations occur when an oscillating system experiences energy loss due to resistive forces like friction or air resistance, causing the amplitude to gradually decrease over time. Coupled oscillations involve two or more oscillators linked in such a way that energy transfers between them, leading to synchronized or complex motion patterns. Understanding these phenomena is crucial in fields such as mechanical engineering, electronics, and wave physics for analyzing system stability and energy distribution.
Fundamental Concepts of Damped Oscillation
Damped oscillation occurs when an oscillatory system experiences a resistive force, such as friction or air resistance, causing the amplitude to decrease exponentially over time. The fundamental concepts include the damping coefficient, which quantifies the rate of energy loss, and the distinction between underdamped, critically damped, and overdamped regimes that determine the system's response. Unlike coupled oscillation, where two or more oscillators influence each other's motion, damped oscillation focuses on the single oscillator's energy dissipation and gradual cessation of motion.
Basics of Coupled Oscillation Explained
Coupled oscillation occurs when two or more oscillators influence each other's motion through a coupling mechanism, resulting in energy transfer between them and the formation of normal modes with distinct frequencies. Unlike damped oscillation, which involves the gradual loss of energy in a single system due to resistive forces, coupled oscillations maintain energy exchange, leading to complex periodic behavior. Understanding the stiffness of the coupling and the natural frequencies of individual oscillators is essential to analyze the behavior and amplitude modulation in coupled oscillation systems.
Key Differences Between Damped and Coupled Oscillations
Damped oscillation involves a single system where energy is gradually lost due to resistive forces like friction or air resistance, causing the amplitude to decrease over time until motion ceases. Coupled oscillation occurs in systems with two or more interconnected oscillators that exchange energy, resulting in complex motion characterized by synchronized or beat frequencies. The key difference lies in energy dissipation in damped oscillations versus energy transfer and interaction between oscillators in coupled oscillations.
Mathematical Modeling of Damped Oscillations
Damped oscillations are mathematically modeled by second-order differential equations incorporating a damping factor, typically expressed as \( m\frac{d^2x}{dt^2} + c\frac{dx}{dt} + kx = 0 \), where \( m \) is mass, \( c \) is the damping coefficient, and \( k \) is the spring constant. The solution to this equation reveals exponential decay in amplitude over time, characterizing underdamped, overdamped, or critically damped motion based on the damping ratio \( \zeta = \frac{c}{2\sqrt{mk}} \). In contrast, coupled oscillations involve multiple masses and springs, leading to systems of differential equations with interaction terms that require matrix methods and eigenvalue analysis for their mathematical modeling.
Mathematical Representation of Coupled Oscillations
Coupled oscillations are mathematically represented by a system of coupled differential equations describing the interaction between oscillators, often modeled as \( m\ddot{x}_1 + kx_1 + k_c(x_1 - x_2) = 0 \) and \( m\ddot{x}_2 + kx_2 + k_c(x_2 - x_1) = 0 \), where \( k_c \) represents the coupling constant. Unlike damped oscillations, which include a damping term \( c\dot{x} \) to account for energy loss, coupled oscillations emphasize energy transfer between oscillators without inherent dissipation. Eigenvalue analysis of the coefficient matrix yields normal mode frequencies, providing insight into the collective oscillatory behavior of the coupled system.
Real-World Applications of Damped Oscillation
Damped oscillation plays a critical role in automotive suspension systems by minimizing vibrations and enhancing ride comfort. This phenomenon is essential in bridge engineering to prevent structural damage from wind or traffic-induced oscillations. In electronic circuits, damped oscillations help stabilize signals in filters and oscillators, ensuring reliable device performance.
Real-World Applications of Coupled Oscillation
Coupled oscillation occurs in systems where two or more oscillators interact, sharing energy and influencing each other's motion, such as in synchronized clapping, coupled pendulums in clocks, and power grid stability. Real-world applications include wireless communication networks where coupled oscillators generate stable frequencies, and in biological systems like heart cells that beat in unison through coupled oscillations. Damped oscillation involves energy loss over time causing amplitude reduction, contrasting with coupled oscillation's energy exchange and synchronization properties vital for engineering and biological timing mechanisms.
Experimental Setups for Comparing Both Oscillations
Experimental setups for damped oscillation typically involve a mass-spring system or pendulum with adjustable damping elements such as air resistance plates or magnetic brakes to quantify energy loss over time. Coupled oscillation experiments use two or more linked oscillators, like coupled pendulums or masses connected by springs, enabling the study of energy transfer and mode synchronization between systems. Precise sensors and motion analysis tools enhance measurement accuracy for frequency, amplitude decay, and phase relationships in both setups, facilitating direct comparison of damping effects and coupling dynamics.
Conclusion: Choosing Between Damped and Coupled Oscillations
Choosing between damped and coupled oscillations depends on the system's energy dissipation and interaction characteristics. Damped oscillations are ideal for systems requiring energy loss management and stabilization, such as shock absorbers and electrical circuits with resistance. Coupled oscillations suit applications involving energy transfer between connected oscillators, like in mechanical watch mechanisms or coupled pendulums, optimizing synchronization and resonance effects.
Damped oscillation Infographic
 libterm.com
libterm.com