The Neper scale measures ratios of quantities such as amplitude or power using a logarithmic scale based on natural logarithms, commonly applied in fields like acoustics and signal processing to describe gain or loss. It provides a direct way to express relative changes without reference to an absolute value, which makes it useful for analyzing signals and systems. Explore the rest of this article to understand how the Neper scale compares to other measurement scales and its practical applications.
Table of Comparison
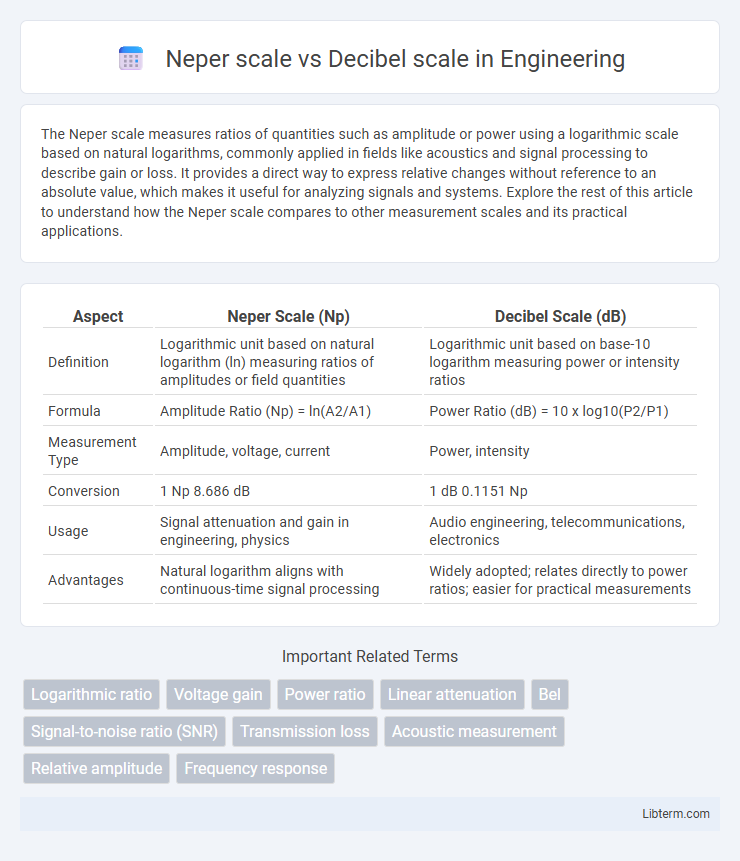
| Aspect | Neper Scale (Np) | Decibel Scale (dB) |
|---|---|---|
| Definition | Logarithmic unit based on natural logarithm (ln) measuring ratios of amplitudes or field quantities | Logarithmic unit based on base-10 logarithm measuring power or intensity ratios |
| Formula | Amplitude Ratio (Np) = ln(A2/A1) | Power Ratio (dB) = 10 x log10(P2/P1) |
| Measurement Type | Amplitude, voltage, current | Power, intensity |
| Conversion | 1 Np 8.686 dB | 1 dB 0.1151 Np |
| Usage | Signal attenuation and gain in engineering, physics | Audio engineering, telecommunications, electronics |
| Advantages | Natural logarithm aligns with continuous-time signal processing | Widely adopted; relates directly to power ratios; easier for practical measurements |
Introduction to Neper and Decibel Scales
The Neper and Decibel scales both measure signal ratios but differ fundamentally in their mathematical basis: the Neper uses natural logarithms and expresses ratios in nepers (Np), while the Decibel employs logarithms base 10 and expresses ratios in decibels (dB). The Neper scale is often used in fields like acoustics and telecommunications for voltage and current ratios, where it provides a direct relationship to exponential signal attenuation or gain. In contrast, the Decibel scale is more widespread in audio engineering and electronics due to its compatibility with power ratios and its intuitive logarithmic representation of sound intensity and signal strength.
Historical Background of Sound Measurement
The Neper scale, introduced by John Napier in the early 17th century, was initially developed for logarithmic calculations but later found application in measuring ratios such as sound intensity. The Decibel scale, created by Bell Laboratories in the 1920s, was specifically designed for quantifying sound levels in telecommunications and acoustics. Both scales utilize logarithmic principles, with the Decibel becoming the standard in audio engineering due to its practical alignment with human hearing sensitivity.
Defining the Neper Scale
The Neper scale measures ratios of amplitudes or field quantities using natural logarithms and represents gain or loss linearly in terms of nepers (Np). Defined as one neper equaling the natural logarithm of the amplitude ratio, it contrasts with the decibel scale, which uses logarithms base 10 and quantifies power ratios. The Neper scale is particularly useful in fields like signal processing and telecommunications for analyzing voltage, current, or electric field strength variations.
Understanding the Decibel Scale
The Decibel (dB) scale quantifies sound intensity and power levels using a logarithmic measurement relative to a reference value, enhancing sensitivity to large dynamic ranges. Unlike the Neper (Np) scale, which uses natural logarithms, the Decibel scale employs base-10 logarithms, making it more intuitive and widely adopted in acoustics, electronics, and telecommunications. Understanding the Decibel scale involves recognizing its ability to express ratios of power or amplitude, where every 10 dB increase corresponds to a tenfold increase in power, facilitating clear signal strength comparisons.
Mathematical Relationships: Neper vs Decibel
The Neper (Np) and Decibel (dB) scales both measure logarithmic ratios, with the Neper based on natural logarithms and the Decibel on base-10 logarithms. The mathematical relationship is defined as 1 Np = 20/log(10) dB 8.686 dB, linking amplitude ratios in Nepers to power ratios in Decibels. This conversion is critical in fields like acoustics and telecommunications where signal attenuation or gain must be accurately quantified across different logarithmic scales.
Applications of the Neper Scale
The Neper scale is primarily used in fields involving exponential growth or decay, such as signal processing and telecommunications, where it quantifies ratios of amplitudes and power using natural logarithms. Unlike the decibel scale, which employs common logarithms and is widely adopted in audio and acoustics, the Neper scale facilitates precise mathematical modeling of wave attenuation and amplification. Its application is particularly critical in microwave engineering and fiber optics for assessing signal loss with direct physical interpretation based on amplitude ratios.
Applications of the Decibel Scale
The decibel scale is widely used in telecommunications, audio engineering, and acoustics due to its logarithmic nature, which effectively represents sound intensity and signal power levels. This scale facilitates the measurement of gain, loss, and noise in electronic circuits, allowing engineers to easily compare and analyze signal strengths. Unlike the neper scale, the decibel scale is more intuitive for practical applications since it aligns closely with human hearing perception and is universally adopted in industry standards.
Key Differences Between Neper and Decibel
The Neper scale measures ratios using natural logarithms, primarily representing amplitude ratios, while the Decibel scale uses base-10 logarithms, commonly quantifying power ratios. Neper values are dimensionless and directly relate to voltage or pressure ratios, whereas Decibels often convert power ratios by a factor of ten and amplitude ratios by twenty. Conversions between the two involve the factor 1 Np 8.686 dB, highlighting their mathematical and application distinctions in signal processing and acoustics.
Conversion Between Neper and Decibel
The Neper (Np) and Decibel (dB) scales measure signal amplitude ratios, with Neper based on natural logarithms and Decibel on base-10 logarithms. To convert between Neper and Decibel, use the relation 1 Np 8.686 dB, derived from 20 log10(e), where e is Euler's number. This conversion is essential in signal processing and telecommunications to translate gain or attenuation values across systems using different logarithmic scales.
Choosing the Right Scale for Your Needs
Neper and decibel scales both measure ratios, but the decibel scale is more commonly used for audio and telecommunications due to its logarithmic nature matching human perception of sound. Neper values express ratios using natural logarithms, making them preferable in mathematical and engineering contexts involving power and amplitude calculations. Choosing the right scale depends on application requirements: decibels suit practical signal level measurements, while nepers are ideal for precise calculations in wave propagation and attenuation studies.
Neper scale Infographic
 libterm.com
libterm.com