Power ratio measures the efficiency between input power and output power in a system, crucial for optimizing performance and energy consumption. Understanding your device's power ratio helps you identify potential losses and improve overall functionality. Explore the rest of this article to learn how to accurately calculate and apply power ratio concepts.
Table of Comparison
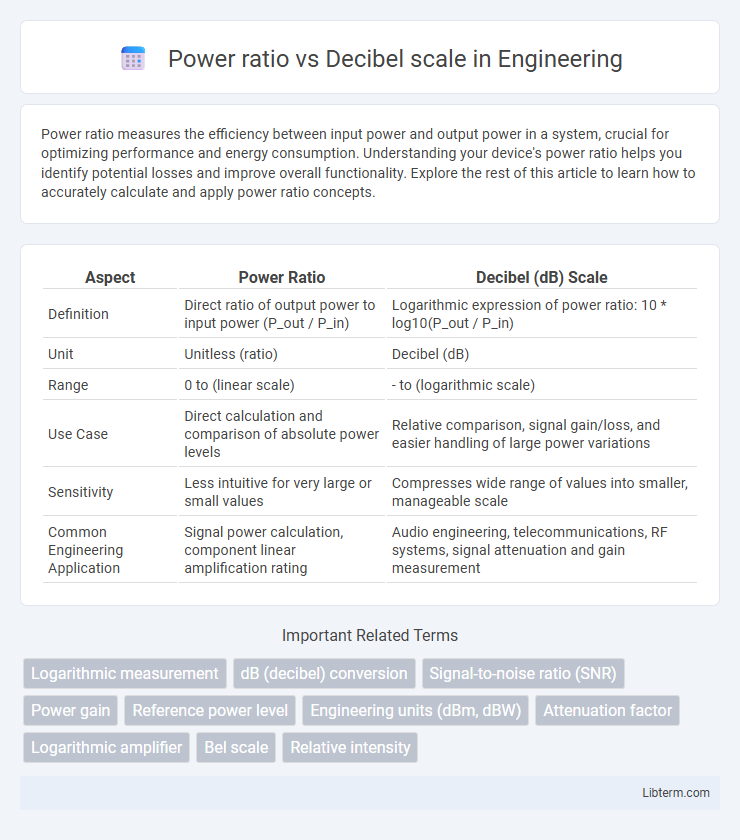
| Aspect | Power Ratio | Decibel (dB) Scale |
|---|---|---|
| Definition | Direct ratio of output power to input power (P_out / P_in) | Logarithmic expression of power ratio: 10 * log10(P_out / P_in) |
| Unit | Unitless (ratio) | Decibel (dB) |
| Range | 0 to (linear scale) | - to (logarithmic scale) |
| Use Case | Direct calculation and comparison of absolute power levels | Relative comparison, signal gain/loss, and easier handling of large power variations |
| Sensitivity | Less intuitive for very large or small values | Compresses wide range of values into smaller, manageable scale |
| Common Engineering Application | Signal power calculation, component linear amplification rating | Audio engineering, telecommunications, RF systems, signal attenuation and gain measurement |
Understanding Power Ratio in Signal Processing
Power ratio in signal processing quantifies the relationship between two power levels, often expressed as a simple numerical value or converted to decibels (dB) for easier interpretation of gain or loss. Unlike linear power ratio, the decibel scale uses a logarithmic transformation, defined as 10 times the base-10 logarithm of the power ratio, allowing for a compact representation of large dynamic ranges. Understanding the power ratio is fundamental in analyzing signal strength, noise levels, and system performance in communication and audio processing applications.
Introduction to the Decibel (dB) Scale
The decibel (dB) scale represents power ratios logarithmically, using the formula dB = 10 log10(P2/P1), where P2 and P1 are power levels. This scale compresses large power ranges into manageable numbers, making it ideal for audio, signal processing, and telecommunications. The logarithmic nature of decibels highlights relative changes, enabling precise measurement of gain, loss, and signal strength compared to linear power ratios.
The Mathematical Relationship: Power Ratio and Decibels
The mathematical relationship between power ratio and decibels expresses power ratio (P2/P1) in logarithmic form as 10 times the base-10 logarithm of the ratio, represented by dB = 10 log10(P2/P1). Decibels provide a convenient scale to compare power levels because they convert multiplicative power ratios into additive values. This relationship is fundamental in fields such as telecommunications and audio engineering for measuring signal strength and attenuation.
Why Use a Logarithmic Scale Like Decibels?
Using a logarithmic scale like decibels efficiently represents the vast range of power ratios encountered in fields such as acoustics and telecommunications, compressing large numerical variations into manageable values. Decibel scales also align with human perception, as the ear responds logarithmically to sound intensity, making decibel measurements more intuitive for measuring audio levels. This scale simplifies multiplication of power ratios into addition, aiding in signal analysis and system design by providing clearer insight into relative changes and cumulative effects.
Calculating Power Ratios Using Decibel Formulas
Calculating power ratios using decibel formulas involves expressing the ratio of two power levels as 10 times the base-10 logarithm of their quotient, represented as dB = 10 log10(P2/P1). The decibel scale effectively compresses large variations in power ratios into a manageable range, making comparisons and signal strength assessments more intuitive. Engineers utilize this logarithmic relationship to analyze amplification, signal loss, and system performance in telecommunications and audio systems.
Practical Examples: Converting Power Ratios to dB
Power ratios are frequently converted to decibel (dB) scale using the formula 10 log10(P2/P1), where P2 and P1 represent power levels. In practical applications like audio engineering, a power increase from 1 watt to 10 watts corresponds to a 10 dB gain, illustrating how decibels quantify power changes logarithmically. Telecommunication systems use similar conversions to express signal strength, where a 100-fold power increase equals a 20 dB rise, emphasizing the scalability and efficiency of the dB scale in real-world scenarios.
Advantages of Decibel Scaling in Engineering Applications
Decibel scaling simplifies the representation of power ratios by converting multiplicative relationships into additive ones, enabling easier analysis and comparison of signal strengths. It compresses wide-ranging values into a manageable scale, facilitating more accurate signal-to-noise ratio assessments and system performance evaluations in engineering fields such as telecommunications and audio engineering. This logarithmic approach also enhances the clarity of graphical data, making it indispensable for monitoring and diagnosing complex electronic systems.
Common Mistakes in Interpreting dB Values
Confusing power ratio and decibel (dB) scale often leads to misinterpretations, as dB is a logarithmic unit representing ratios, not absolute values. A common mistake is neglecting that a 3 dB increase corresponds to approximately doubling the power ratio, while a 10 dB increase indicates a tenfold increase. Misreading dB values without understanding their logarithmic nature can cause significant errors in signal strength and audio level analysis.
Power Ratio vs Voltage Ratio in dB Calculations
Power ratio in decibel (dB) calculations is defined as 10 times the base-10 logarithm of the power ratio (P2/P1), whereas voltage ratio in dB is calculated as 20 times the base-10 logarithm of the voltage ratio (V2/V1) due to power being proportional to the square of voltage. This distinction arises because power is proportional to the square of voltage over a constant resistance, making the voltage ratio expressible in dB by doubling the log value. Correct application of these formulas is critical in fields like electronics and signal processing to accurately quantify gains and losses.
Key Applications of Power Ratio and Decibel Scale in Real World
Power ratio and decibel scale are essential in telecommunications for measuring signal strength, where decibels provide a logarithmic representation simplifying large range comparisons. In audio engineering, decibel scales quantify sound levels, enabling precise calibration of equipment and noise control. Electrical engineers use power ratios to assess amplifier gains and losses, with decibel measurements facilitating standardized evaluations of system performance.
Power ratio Infographic
 libterm.com
libterm.com