The Peaucellier-Lipkin linkage is a mechanical device that converts rotary motion into perfect straight-line motion without the need for sliding guides. It consists of a series of connected rods arranged in a specific geometric pattern, ensuring precise and reliable linear movement ideal for engineering applications. Discover how this ingenious mechanism can enhance your understanding of mechanical linkages by exploring the detailed explanations ahead.
Table of Comparison
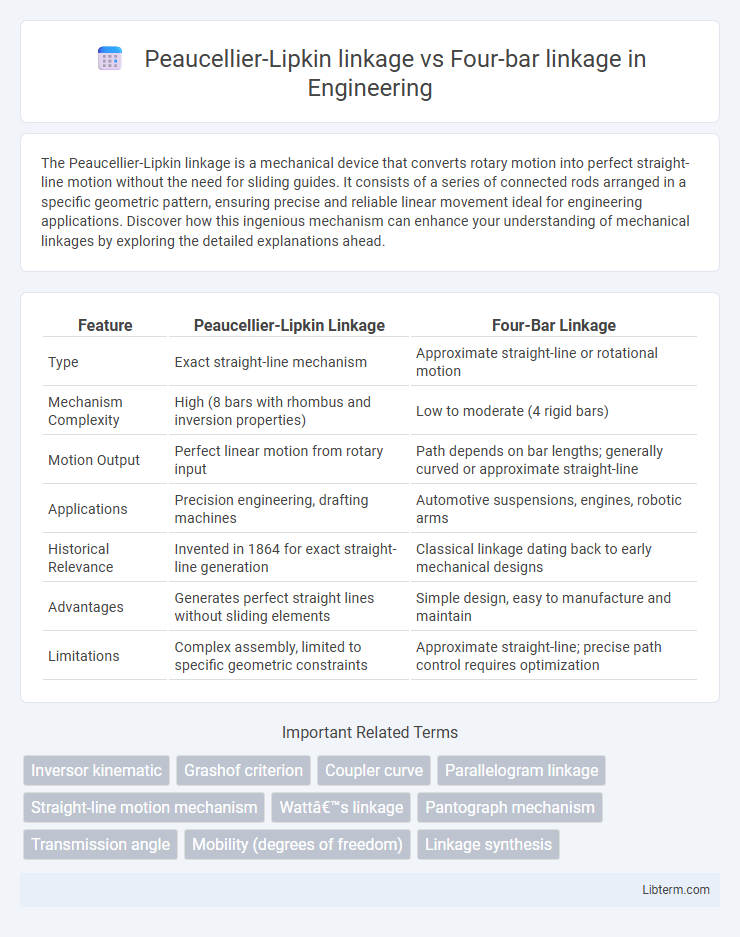
| Feature | Peaucellier-Lipkin Linkage | Four-Bar Linkage |
|---|---|---|
| Type | Exact straight-line mechanism | Approximate straight-line or rotational motion |
| Mechanism Complexity | High (8 bars with rhombus and inversion properties) | Low to moderate (4 rigid bars) |
| Motion Output | Perfect linear motion from rotary input | Path depends on bar lengths; generally curved or approximate straight-line |
| Applications | Precision engineering, drafting machines | Automotive suspensions, engines, robotic arms |
| Historical Relevance | Invented in 1864 for exact straight-line generation | Classical linkage dating back to early mechanical designs |
| Advantages | Generates perfect straight lines without sliding elements | Simple design, easy to manufacture and maintain |
| Limitations | Complex assembly, limited to specific geometric constraints | Approximate straight-line; precise path control requires optimization |
Introduction to Mechanical Linkages
The Peaucellier-Lipkin linkage is a mechanical linkage known for converting rotary motion into perfect straight-line motion, employing a unique arrangement of rods forming a rhombus and a fixed point, making it a milestone in kinematic synthesis. The Four-bar linkage, composed of four rigid bars connected by pivot joints, provides versatile planar motion, enabling a wide range of movements such as oscillation, rotation, and complex paths in mechanical systems. Both linkages serve fundamental roles in mechanical engineering, demonstrating key principles of constrained motion and the transformation of input movement into desired output trajectories.
Overview of Peaucellier-Lipkin Linkage
The Peaucellier-Lipkin linkage is a planar mechanism that converts rotary motion into perfect straight-line motion without relying on sliding guides, distinguishing it from the Four-bar linkage which approximates straight-line paths. This linkage consists of a complex configuration of rods arranged to maintain a precise geometric constraint, enabling exact linear tracing. Its unique design offers superior accuracy in applications requiring flawless linear motion, making it essential in certain mechanical engineering and kinematic tasks.
Overview of Four-Bar Linkage
The four-bar linkage consists of four rigid bars connected by pivot joints forming a closed loop, commonly used to convert rotational motion into complex planar motion. Its simplicity and versatility make it a fundamental mechanism in mechanical engineering applications such as engines, robotic arms, and suspension systems. Unlike the Peaucellier-Lipkin linkage, which generates exact straight-line motion, the four-bar linkage achieves approximate straight-line paths and diverse motion profiles depending on link length ratios.
Historical Development and Applications
The Peaucellier-Lipkin linkage, invented in 1864 by Charles-Nicolas Peaucellier and Yom Tov Lipman Lipkin, marked a key breakthrough as the first planar straight-line mechanism converting rotary motion into perfect linear motion, outperforming earlier approximate solutions like the four-bar linkage developed earlier in the 19th century by Franz Reuleaux. While the four-bar linkage features simpler construction and versatility, facilitating uses in engines, pumps, and robotics for approximate straight-line paths, the Peaucellier-Lipkin linkage found niche applications requiring high precision straight-line guidance, such as in the early design of planimeters and drafting machinery. The two linkages exemplify the evolution from practical mechanical approximations to mathematically exact mechanisms, influencing modern kinematic synthesis and engineering design.
Principle of Straight-Line Motion
The Peaucellier-Lipkin linkage achieves exact straight-line motion through the inversion principle, converting circular motion into perfect linear displacement without approximation. In contrast, the Four-bar linkage generates approximate straight-line motion via coupler curves, relying on specific geometric configurations for near-linear paths. The Peaucellier-Lipkin mechanism's precise straight-line output is critical in applications demanding high accuracy, whereas Four-bar linkages offer simpler construction with less exact linear motion.
Kinematic Analysis: Peaucellier-Lipkin vs Four-Bar
Peaucellier-Lipkin linkage provides an exact straight-line motion using a complex geometric inversion mechanism, making it ideal for precise path generation in kinematic applications. In contrast, the Four-bar linkage offers approximate straight-line motion or other controlled trajectories with simpler construction and easier analysis, relying on the relative angular displacements of its links. Kinematic analysis of the Peaucellier-Lipkin linkage involves nonlinear geometric transformations ensuring exact rectilinear output, whereas Four-bar linkage analysis utilizes loop-closure equations and Grashof conditions for determining range of motion and input-output angular relations.
Advantages and Limitations of Peaucellier-Lipkin Linkage
The Peaucellier-Lipkin linkage provides exact straight-line motion by transforming circular motion into perfect linear motion, a significant advantage over the approximate straight-line trajectory of the four-bar linkage. Its design enables high precision in applications such as drafting machines and mechanical linkages where exact geometry is critical. However, the Peaucellier-Lipkin linkage is more complex, bulkier, and less practical for compact or high-speed mechanisms due to the higher number of links and joints involved.
Advantages and Limitations of Four-Bar Linkage
The Four-bar linkage offers simplicity, ease of analysis, and compact design, making it widely used in mechanical systems for converting rotational motion into complex paths. Its limitations include restricted motion types, limited precision for exact straight-line generation, and potential issues with linkage interference or singular configurations. Despite these, its robustness and versatility in applications like engine mechanisms and robotic arms make it a foundational mechanism in mechanical engineering.
Comparative Performance and Use Cases
The Peaucellier-Lipkin linkage offers perfect straight-line motion ideal for precision applications such as drafting machines and mechanical plotters, outperforming the Four-bar linkage which typically generates approximate straight paths better suited for simpler, less precise mechanical tasks like linkages in engines or robotic arms. While the Four-bar linkage excels in versatility and ease of design for a wide range of mechanical movements including oscillations and rotations, the Peaucellier-Lipkin's complex geometry limits its use to specialized scenarios demanding exact linear output. Engineering applications requiring exact linearity and minimal error prioritize Peaucellier-Lipkin mechanisms, whereas those prioritizing cost, simplicity, and flexibility commonly implement Four-bar linkages.
Future Trends in Mechanical Linkage Design
Emerging research in mechanical linkage design emphasizes increased precision and adaptability, with Peaucellier-Lipkin linkages offering perfect straight-line motion vital for advanced robotics and micro-mechanical systems. Four-bar linkages continue to dominate due to their simplicity and versatility but face integration challenges with smart materials and actuators aimed at enhancing responsiveness and energy efficiency. Future trends indicate hybrid systems combining the Peaucellier-Lipkin's geometric exactness with the four-bar linkage's robustness for optimized performance in automation and biomedical devices.
Peaucellier-Lipkin linkage Infographic
 libterm.com
libterm.com