Torsion refers to the twisting of an object due to an applied torque, causing shear stress and deformation within its material. It plays a crucial role in engineering and mechanics, influencing the design of shafts, beams, and structural components to ensure safety and functionality. Explore the full article to understand how torsion impacts your designs and applications.
Table of Comparison
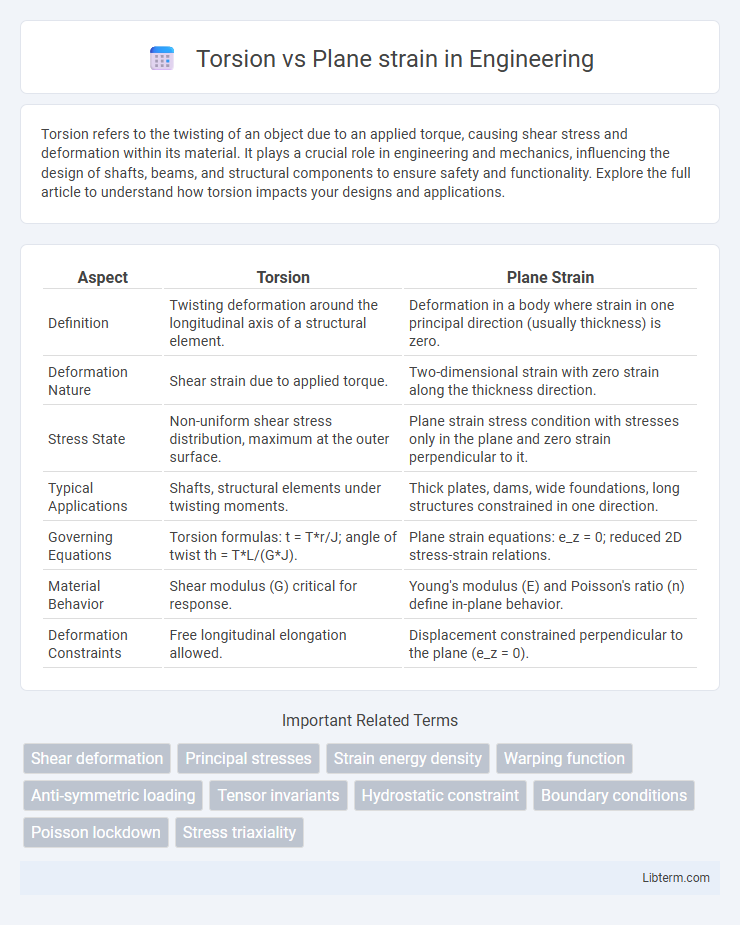
| Aspect | Torsion | Plane Strain |
|---|---|---|
| Definition | Twisting deformation around the longitudinal axis of a structural element. | Deformation in a body where strain in one principal direction (usually thickness) is zero. |
| Deformation Nature | Shear strain due to applied torque. | Two-dimensional strain with zero strain along the thickness direction. |
| Stress State | Non-uniform shear stress distribution, maximum at the outer surface. | Plane strain stress condition with stresses only in the plane and zero strain perpendicular to it. |
| Typical Applications | Shafts, structural elements under twisting moments. | Thick plates, dams, wide foundations, long structures constrained in one direction. |
| Governing Equations | Torsion formulas: t = T*r/J; angle of twist th = T*L/(G*J). | Plane strain equations: e_z = 0; reduced 2D stress-strain relations. |
| Material Behavior | Shear modulus (G) critical for response. | Young's modulus (E) and Poisson's ratio (n) define in-plane behavior. |
| Deformation Constraints | Free longitudinal elongation allowed. | Displacement constrained perpendicular to the plane (e_z = 0). |
Introduction to Torsion and Plane Strain
Torsion refers to the twisting of an object due to an applied torque, causing shear stress over the cross-section, commonly analyzed in shafts and cylindrical structures under rotational forces. Plane strain describes a two-dimensional deformation state where strain in one principal direction (usually thickness) is negligible, typically observed in long structures such as dams or tunnels where deformation is constrained. Understanding the fundamental differences between torsion-induced shear stresses and plane strain conditions is crucial for accurately predicting stress distribution and material behavior in engineering applications.
Fundamental Concepts and Definitions
Torsion refers to the twisting of an object due to an applied torque, resulting in shear stresses and angular deformation along the longitudinal axis. Plane strain describes a deformation state where strain in one principal direction is zero, typically used in scenarios like thick-walled cylinders or long structures where out-of-plane deformation is constrained. Understanding the distinctions between torsion-induced shear stresses and plane strain's constrained deformation is crucial in elasticity and structural analysis.
Key Differences Between Torsion and Plane Strain
Torsion involves twisting a structural element around its longitudinal axis, generating shear stress and angle deformation, whereas plane strain refers to deformation in a two-dimensional plane with negligible strain in the perpendicular direction. In torsion, shear stress distribution is crucial, while plane strain primarily concerns normal stresses and strains within the constrained plane. Material response under torsion emphasizes shear modulus, but plane strain analysis focuses on Young's modulus and Poisson's ratio for stress-strain relationships.
Stress Distribution in Torsion vs Plane Strain
Stress distribution in torsion is characterized by shear stresses that vary linearly from zero at the center to a maximum at the outer surface, following a circular pattern around the axis of the shaft. Plane strain, in contrast, involves stress components primarily in two dimensions, with normal stresses dominating and restricted deformation in the third dimension, leading to uniform strain along the constrained direction. Understanding these differences is crucial for accurately predicting failure modes and designing structural elements subjected to complex loading conditions.
Deformation Characteristics
Torsion deformation involves shear stresses causing angular displacement and twisting of cylindrical or circular cross-section materials, resulting in warping and non-uniform strain distribution. Plane strain deformation restricts strain in one direction, producing linearized strain patterns and predominantly normal stresses with minimal shear, common in thick bodies under compression. Understanding these distinct deformation characteristics aids in predicting material behavior under complex loading conditions and optimizing design for structural integrity.
Common Applications in Engineering
Torsion is primarily applied in engineering designs involving shafts, drive trains, and structural members subjected to twisting forces, such as in automotive axles and helicopter rotor blades. Plane strain conditions are common in geotechnical engineering for analyzing soil deformation and in the design of thick-walled pressure vessels where deformation in one dimension is constrained. Both concepts are critical for ensuring structural integrity and performance in materials subjected to specific loading scenarios.
Material Behavior Under Torsion and Plane Strain
Material behavior under torsion involves shear stress distribution across the cross-section, causing angular deformation mainly governed by shear modulus and yield strength in shear. In plane strain, deformation is constrained in one direction, leading to biaxial stress states with dominant normal stresses and minimal lateral strain, significantly affecting the material's yield and failure characteristics. Understanding the difference in stress-strain responses under these conditions is critical for accurate modeling of ductility and fracture in metals and composites.
Analysis Methods and Mathematical Models
Torsion analysis typically employs Saint-Venant's theory, using polar moment of inertia and shear stress distribution models to predict angular deformation in circular shafts. Plane strain problems utilize two-dimensional elasticity solutions and Airy stress functions, simplifying three-dimensional stress states under constrained strain conditions along one axis. Finite Element Methods (FEM) are widely applied for complex geometries in both torsion and plane strain analyses, enabling numerical approximation of stress-strain responses using element discretization and boundary condition formulations.
Key Factors Affecting Performance
Torsion performance is primarily influenced by material shear strength, cross-sectional geometry, and the distribution of shear stresses, while plane strain behavior depends on the modulus of elasticity, Poisson's ratio, and in-plane stress constraints. The deformation in torsion involves twisting along the axis causing shear strain, whereas plane strain conditions restrict deformation perpendicular to the strain plane, affecting stress distribution and failure modes. Key factors such as boundary conditions, load application, and material anisotropy critically define the response and durability in both torsion and plane strain scenarios.
Choosing Between Torsion and Plane Strain in Design
Choosing between torsion and plane strain in design depends on the loading conditions and geometry of the component. Torsion is essential for shafts and circular elements subjected to twisting moments, where shear stress distribution around the axis must be analyzed. Plane strain is ideal for long, prismatic structures under uniaxial loading, enabling simplification of stress analysis in two dimensions while assuming negligible strain in the out-of-plane direction.
Torsion Infographic
 libterm.com
libterm.com