The Arbitrary Lagrangian-Eulerian (ALE) approach combines the advantages of both Lagrangian and Eulerian frameworks to efficiently handle problems involving fluid-structure interaction and large deformations. This method allows the mesh to move independently of the material, providing greater flexibility and accuracy in simulating complex physical phenomena. Discover how the ALE approach can enhance your computational models by exploring the detailed applications and benefits in the article below.
Table of Comparison
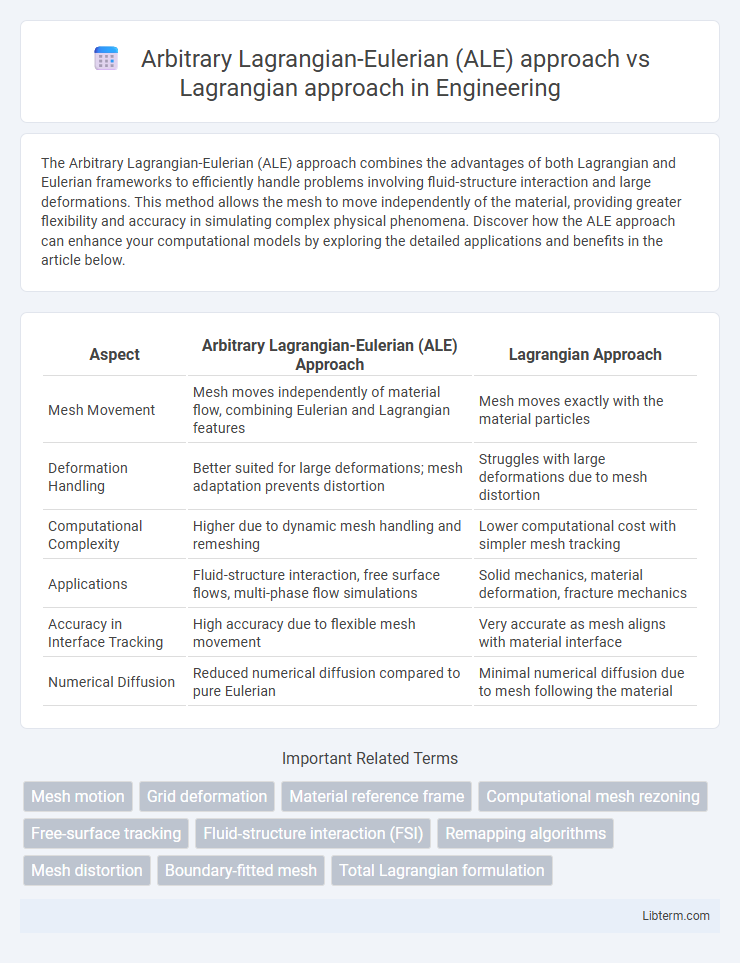
| Aspect | Arbitrary Lagrangian-Eulerian (ALE) Approach | Lagrangian Approach |
|---|---|---|
| Mesh Movement | Mesh moves independently of material flow, combining Eulerian and Lagrangian features | Mesh moves exactly with the material particles |
| Deformation Handling | Better suited for large deformations; mesh adaptation prevents distortion | Struggles with large deformations due to mesh distortion |
| Computational Complexity | Higher due to dynamic mesh handling and remeshing | Lower computational cost with simpler mesh tracking |
| Applications | Fluid-structure interaction, free surface flows, multi-phase flow simulations | Solid mechanics, material deformation, fracture mechanics |
| Accuracy in Interface Tracking | High accuracy due to flexible mesh movement | Very accurate as mesh aligns with material interface |
| Numerical Diffusion | Reduced numerical diffusion compared to pure Eulerian | Minimal numerical diffusion due to mesh following the material |
Introduction to Computational Mechanics Methods
The Arbitrary Lagrangian-Eulerian (ALE) approach combines the mesh-moving advantages of the Lagrangian method with the fixed spatial reference of the Eulerian method, enabling better handling of large deformations and fluid-structure interactions in computational mechanics. Unlike the purely Lagrangian approach, which tracks material particles and often suffers from mesh distortion in large strain problems, ALE allows mesh movement independent of material flow, improving accuracy and stability in simulations. This flexibility makes ALE particularly effective in computational mechanics methods involving complex multiphysics problems such as metal forming, fluid flow, and wave propagation.
Overview of the Lagrangian Approach
The Lagrangian approach tracks individual material particles by following their trajectories through time, making it ideal for problems involving large deformations and complex material interfaces. This method offers precise mesh deformation control, enhancing accuracy in simulations of solid mechanics, fluid-structure interactions, and fracture dynamics. However, it may suffer from mesh distortion in cases of extreme deformation, limiting computational stability and requiring remeshing techniques.
Fundamentals of the Arbitrary Lagrangian-Eulerian (ALE) Formalism
The Arbitrary Lagrangian-Eulerian (ALE) formalism integrates the Lagrangian and Eulerian frameworks by allowing mesh movement to be independent of material flow, enhancing computational flexibility in fluid-structure interaction problems. Unlike the purely Lagrangian approach, where the mesh moves with the material, ALE introduces a mesh velocity field that can be arbitrarily specified, optimizing mesh quality and reducing distortion. This approach is fundamental in solving nonlinear dynamics and multiphase flows, providing improved accuracy and stability compared to traditional fixed or fully material-bound meshes.
Mathematical Formulations: Lagrangian vs ALE
The Lagrangian approach tracks mesh nodes moving with material flow, resulting in equations formulated solely in material coordinates, leading to strong coupling between geometry and deformation. The Arbitrary Lagrangian-Eulerian (ALE) approach introduces an independent mesh velocity field, allowing mesh motion to differ from material motion and decoupling mesh deformation from physical deformation. This flexibility in ALE modifies the governing equations by incorporating mesh velocity terms, enhancing numerical stability and accuracy in problems with large deformations compared to the purely Lagrangian framework.
Handling Mesh Deformation: Lagrangian and ALE Comparison
The Arbitrary Lagrangian-Eulerian (ALE) approach enables controlled mesh deformation by allowing mesh nodes to move independently from material motion, effectively minimizing mesh distortion in complex flow simulations. In contrast, the pure Lagrangian approach moves the mesh with the material, often leading to severe mesh distortion and numerical inaccuracies in problems involving large deformations. ALE methods preserve mesh quality by combining Lagrangian motion with Eulerian remeshing or smoothing techniques, enhancing stability and accuracy in fluid-structure interaction and multiphase flow analyses.
Application Scenarios and Use Cases
The Arbitrary Lagrangian-Eulerian (ALE) approach excels in complex fluid-structure interaction problems, such as in automotive crash simulations and biomedical device modeling, where it effectively manages mesh distortion by combining both Lagrangian and Eulerian frameworks. The pure Lagrangian approach is ideal for solid mechanics and metal forming processes, where tracking material deformation without mesh entanglement is crucial. ALE is preferred in applications involving large deformations and moving boundaries, while the Lagrangian method suits scenarios requiring precise material interface tracking and strain history.
Advantages and Limitations of Each Approach
The Arbitrary Lagrangian-Eulerian (ALE) approach offers significant advantages in handling large deformations and fluid-structure interactions by combining mesh movement flexibility with computational stability, making it ideal for complex simulations involving both fluids and solids. In contrast, the pure Lagrangian approach excels in tracking material interfaces and deformation history with high accuracy but struggles with mesh distortion during large deformations and complex flow scenarios. While ALE reduces mesh tangling through grid adaptation, it introduces higher computational complexity, whereas the Lagrangian method maintains simpler implementation at the expense of robustness in highly dynamic environments.
Numerical Stability and Accuracy Analysis
The Arbitrary Lagrangian-Eulerian (ALE) approach enhances numerical stability by allowing mesh motion to adapt dynamically, reducing mesh distortion commonly encountered in pure Lagrangian simulations and thereby maintaining higher accuracy in tracking fluid-structure interfaces. Lagrangian methods track material deformation directly but often suffer from mesh tangling and numerical instability in large deformation scenarios, decreasing solution accuracy. Comparative analyses highlight ALE's superior ability to balance mesh quality and solution fidelity, particularly in complex transient flow problems requiring precise interface capture.
Computational Efficiency and Resource Requirements
The Arbitrary Lagrangian-Eulerian (ALE) approach offers enhanced computational efficiency over the purely Lagrangian method by allowing mesh deformation to be controlled independently from material motion, reducing mesh distortion and the need for frequent remeshing. This flexibility leads to lower computational resource requirements as ALE can maintain mesh quality and stability in complex simulations with large deformations, whereas the Lagrangian approach often incurs higher costs due to mesh entanglement and refinement processes. Consequently, ALE is generally preferred in applications requiring a balance between accuracy and computational expense, such as fluid-structure interaction and large-deformation solid mechanics.
Future Trends in Mesh-Based Simulation Methods
Future trends in mesh-based simulation methods emphasize enhancing adaptability and accuracy through the Arbitrary Lagrangian-Eulerian (ALE) approach, which combines the strengths of both Lagrangian and Eulerian frameworks to manage mesh distortion and fluid-structure interactions more effectively. The ALE method's ability to dynamically adjust mesh motion independently from material flow positions it as a pivotal technique for complex multiphysics simulations, offering significant improvements over the purely Lagrangian approach that struggles with severe mesh distortion. Advances in computational algorithms and high-performance computing are expected to further optimize ALE simulations, enabling real-time, high-fidelity analysis in fields such as aerospace, biomechanics, and geophysics.
Arbitrary Lagrangian-Eulerian (ALE) approach Infographic
 libterm.com
libterm.com