The steady-state response describes how a system behaves after initial transients have settled, maintaining consistent output under constant input conditions. This concept is crucial for understanding system stability and performance in engineering and signal processing. Explore the rest of the article to learn how the steady-state response impacts your system design and analysis.
Table of Comparison
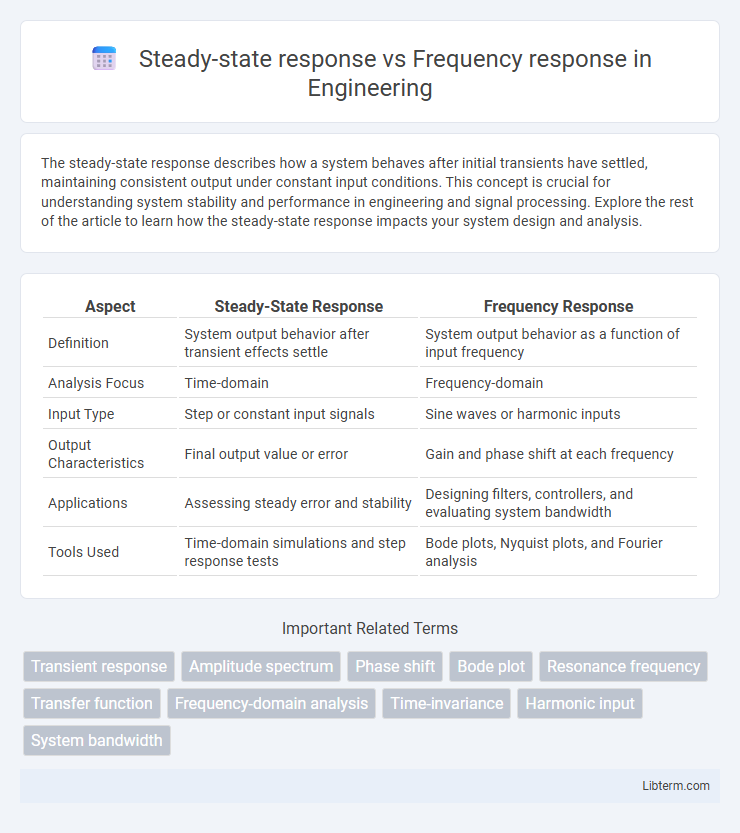
| Aspect | Steady-State Response | Frequency Response |
|---|---|---|
| Definition | System output behavior after transient effects settle | System output behavior as a function of input frequency |
| Analysis Focus | Time-domain | Frequency-domain |
| Input Type | Step or constant input signals | Sine waves or harmonic inputs |
| Output Characteristics | Final output value or error | Gain and phase shift at each frequency |
| Applications | Assessing steady error and stability | Designing filters, controllers, and evaluating system bandwidth |
| Tools Used | Time-domain simulations and step response tests | Bode plots, Nyquist plots, and Fourier analysis |
Introduction to Steady-State and Frequency Response
Steady-state response refers to a system's behavior after initial transients have settled, showing how the output stabilizes under a constant or periodic input. Frequency response characterizes how a system reacts to inputs of varying frequencies, highlighting amplitude and phase changes across the frequency spectrum. Understanding these concepts is crucial for analyzing system performance in control theory and signal processing.
Definitions: Steady-State Response vs Frequency Response
Steady-state response refers to the behavior of a system after transient effects have settled, representing its output when subjected to a constant or sinusoidal input over time. Frequency response describes how a system reacts to different input frequencies, detailing the amplitude and phase of the output relative to the input frequency. These definitions distinguish steady-state response as a time-domain concept and frequency response as a frequency-domain characterization of system behavior.
Importance in System Analysis
Steady-state response and frequency response are fundamental in system analysis for evaluating system behavior under continuous inputs and varying frequencies, respectively. Steady-state response provides insight into the long-term output stability when subjected to constant or sinusoidal inputs, crucial for ensuring system reliability. Frequency response reveals how a system amplifies or attenuates signals across different frequencies, enabling the design of filters and control systems to achieve desired performance characteristics.
Mathematical Representation
Steady-state response in linear systems is mathematically expressed by evaluating the system's output when subjected to a sinusoidal input at a specific frequency, often represented as \( y(t) = |H(j\omega)| \cos(\omega t + \angle H(j\omega)) \), where \( H(j\omega) \) is the system's frequency response function. Frequency response characterizes the system's behavior over a range of frequencies using the transfer function \( H(j\omega) = \frac{Y(j\omega)}{X(j\omega)} \), relating output and input in the frequency domain. The frequency response provides the amplitude ratio \( |H(j\omega)| \) and phase shift \( \angle H(j\omega) \), which dictate the steady-state sinusoidal output for each input frequency \(\omega\).
Steady-State Response in Time Domain
Steady-state response in the time domain refers to the behavior of a system as it reaches a consistent output after transient effects have decayed, reflecting how the system responds to a continuous input signal over time. It is crucial for understanding the long-term performance of linear time-invariant (LTI) systems, especially in the presence of sinusoidal or periodic inputs. This response can be characterized by parameters such as amplitude, phase shift, and steady-state error, which are essential in control system analysis and design.
Frequency Response in Frequency Domain
Frequency response in the frequency domain characterizes how a system reacts to different input frequencies, revealing magnitude and phase shifts across the spectrum. It provides a crucial understanding of system stability and performance by analyzing the transfer function's behavior at various frequencies. Engineers use frequency response methods, such as Bode plots and Nyquist plots, to design and optimize control systems, filters, and signal processing circuits.
Key Differences between Steady-State and Frequency Response
Steady-state response represents the long-term output of a system when subjected to a constant or sinusoidal input, showing how the system stabilizes over time. Frequency response characterizes how the system's output amplitude and phase vary with input signal frequency, providing insight into bandwidth and resonance behaviors. Key differences include steady-state response focusing on time-domain behavior at specific inputs while frequency response analyzes system behavior across a spectrum of frequencies, essential for control system design and signal processing.
Applications in Engineering and Control Systems
Steady-state response is critical in control systems for determining the long-term behavior of a system under constant input conditions, enabling engineers to design controllers that ensure desired output stability and accuracy. Frequency response analysis is essential for assessing system robustness and stability across different input frequencies, facilitating the design of filters, compensators, and resonance avoidance in mechanical and electrical engineering applications. Both methods are integral in optimizing system performance, particularly in servo mechanisms, signal processing, and vibration control within control engineering.
Advantages and Limitations of Each Approach
Steady-state response analysis provides clear insight into system behavior under constant or sinusoidal inputs, allowing straightforward prediction of long-term output but may overlook transient phenomena and time-varying dynamics. Frequency response analysis excels in characterizing how systems react across a spectrum of frequencies, facilitating robust design and stability assessment, yet it can be limited by assumptions of linearity and may not capture nonlinear effects or system parameter variations. Combining both techniques often yields a comprehensive understanding, balancing precise steady-state predictions with broad frequency-dependent performance insights.
Summary and Practical Insights
Steady-state response analyzes how a system behaves under constant or periodic inputs over time, revealing its long-term output characteristics, while frequency response measures the system's output amplitude and phase across a range of input frequencies. Understanding the steady-state response is crucial for time-domain applications, whereas frequency response is essential in designing filters, controllers, and communication systems. Practical insights emphasize leveraging frequency response techniques like Bode plots and Nyquist diagrams to predict system stability and optimize performance in signal processing and control engineering.
Steady-state response Infographic
 libterm.com
libterm.com