Nonlinear control addresses complex systems where traditional linear methods fail due to variable dynamics and feedback loops. It involves advanced mathematical techniques to ensure system stability and performance under changing conditions. Discover how mastering nonlinear control can enhance Your ability to manage dynamic systems effectively in the full article.
Table of Comparison
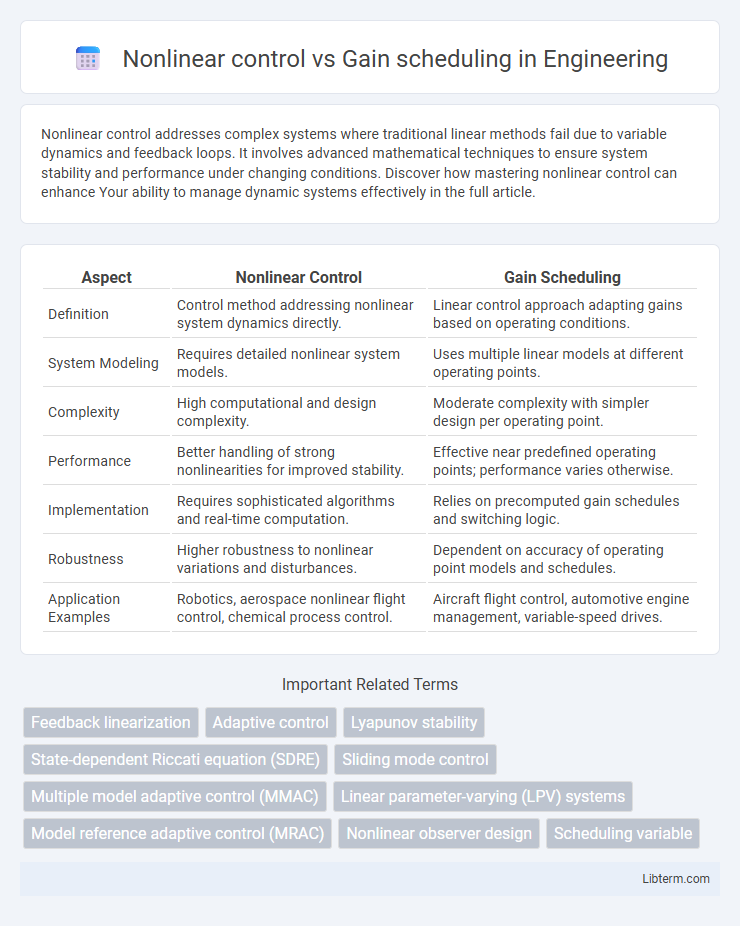
| Aspect | Nonlinear Control | Gain Scheduling |
|---|---|---|
| Definition | Control method addressing nonlinear system dynamics directly. | Linear control approach adapting gains based on operating conditions. |
| System Modeling | Requires detailed nonlinear system models. | Uses multiple linear models at different operating points. |
| Complexity | High computational and design complexity. | Moderate complexity with simpler design per operating point. |
| Performance | Better handling of strong nonlinearities for improved stability. | Effective near predefined operating points; performance varies otherwise. |
| Implementation | Requires sophisticated algorithms and real-time computation. | Relies on precomputed gain schedules and switching logic. |
| Robustness | Higher robustness to nonlinear variations and disturbances. | Dependent on accuracy of operating point models and schedules. |
| Application Examples | Robotics, aerospace nonlinear flight control, chemical process control. | Aircraft flight control, automotive engine management, variable-speed drives. |
Introduction to Nonlinear Control and Gain Scheduling
Nonlinear control techniques address the complexities of systems with nonlinear dynamics by directly incorporating system nonlinearities into the control design, improving performance and stability over a wide operating range. Gain scheduling involves designing multiple linear controllers at different operating points and switching or interpolating between them based on system parameters, providing a practical approach for handling certain nonlinear behaviors. While nonlinear control offers robustness and precision by considering the full nonlinear model, gain scheduling simplifies implementation and is effective for systems with slowly varying parameters.
Fundamental Concepts in Nonlinear Control
Nonlinear control fundamentally addresses system behaviors that cannot be accurately modeled by linear equations, using techniques such as Lyapunov stability and feedback linearization to ensure robust performance across variable operating conditions. Gain scheduling adapts linear control parameters based on a measurable system variable, effectively approximating nonlinear dynamics through a series of linear controllers. Understanding the intrinsic nonlinearities and stability criteria is crucial for designing controllers that maintain system equilibrium and performance beyond the linear domain.
Overview of Gain Scheduling Techniques
Gain scheduling techniques involve the adjustment of controller parameters based on measurable operating conditions, enabling effective management of nonlinear system behaviors by interpolating between linear models at various operating points. This method utilizes a family of linear controllers designed for different regimes of the nonlinear plant, ensuring stability and performance over a wide range of system dynamics. Common approaches include interpolation, lookup tables, and parameter-dependent controller formulations tailored to evolving system states or outputs.
Key Differences Between Nonlinear Control and Gain Scheduling
Nonlinear control directly addresses system nonlinearities through feedback laws designed for the entire operating range, ensuring stability and performance without segmentation. Gain scheduling divides the operating range into multiple linear models, applying linear controllers at each point and interpolating gains based on scheduling variables, which may compromise robustness in rapid transitions. Nonlinear control offers global stability guarantees, while gain scheduling provides simpler implementation but relies on accurate interpolation and may lack stability assurances outside predefined regions.
Advantages of Nonlinear Control Methods
Nonlinear control methods offer superior performance by directly addressing system nonlinearities, enabling enhanced stability and robustness in complex dynamic environments. These methods reduce dependence on multiple linear models and avoid the pitfalls of model mismatch common in gain scheduling approaches. Furthermore, nonlinear control provides accurate handling of large operating range variations, which improves control precision and efficiency across diverse conditions.
Benefits and Limitations of Gain Scheduling
Gain scheduling offers a practical approach to controlling nonlinear systems by dividing the operating range into multiple linear models, allowing for simpler controller design across various conditions. Its benefits include straightforward implementation and improved performance when system dynamics change predictably with parameters, making it ideal for aerospace and automotive applications. Limitations arise from potential stability issues during transitions between models and the need for extensive system knowledge to define appropriate scheduling variables accurately.
Practical Applications: Where Each Method Excels
Nonlinear control excels in applications requiring precise handling of complex system dynamics such as robotics, aerospace, and automotive systems with significant model nonlinearities. Gain scheduling proves effective in control systems with varying operating conditions, like gas turbines and aircraft engines, where the system can be linearized around multiple operating points. Practical implementation in aerospace often combines both methods, using gain scheduling for broad operating regimes and nonlinear control for fine-tuned stability and performance.
Design Complexity and Implementation Challenges
Nonlinear control involves complex mathematical models and requires advanced algorithms to handle system nonlinearities, resulting in higher design complexity compared to gain scheduling. Gain scheduling simplifies implementation by using multiple linear controllers switched based on operating conditions, but it demands accurate scheduling parameter identification and careful interpolation to maintain stability. Both approaches face challenges in tuning and robustness; however, nonlinear control often demands more computational resources and deeper expertise during implementation.
Performance and Robustness Considerations
Nonlinear control techniques provide superior performance by directly addressing system nonlinearities, resulting in enhanced accuracy and stability across a wide operating range. Gain scheduling improves robustness by adjusting controller parameters based on operating conditions, but may suffer from performance degradation near switching points or unmodeled dynamics. Careful design and analysis are essential to balance the trade-offs between performance optimization and robustness in nonlinear control versus gain scheduling approaches.
Future Trends in Nonlinear and Gain Scheduled Control
Future trends in nonlinear control emphasize the integration of machine learning algorithms and real-time adaptive capabilities to enhance system robustness and performance in complex environments. Gain scheduling techniques are evolving through advanced parameter estimation methods and switching strategies that enable smoother transitions across operating regimes. Emerging research highlights hybrid control frameworks combining nonlinear control's flexibility with gain scheduling's structured approach for improved stability and efficiency in aerospace and automotive applications.
Nonlinear control Infographic
 libterm.com
libterm.com