Modal analysis reveals the natural vibration frequencies and mode shapes of a structure, essential for predicting its dynamic behavior under various loads. Understanding these modes helps you optimize design for stability and prevent resonant conditions that may lead to failure. Explore the rest of the article to learn how modal analysis can enhance your engineering projects.
Table of Comparison
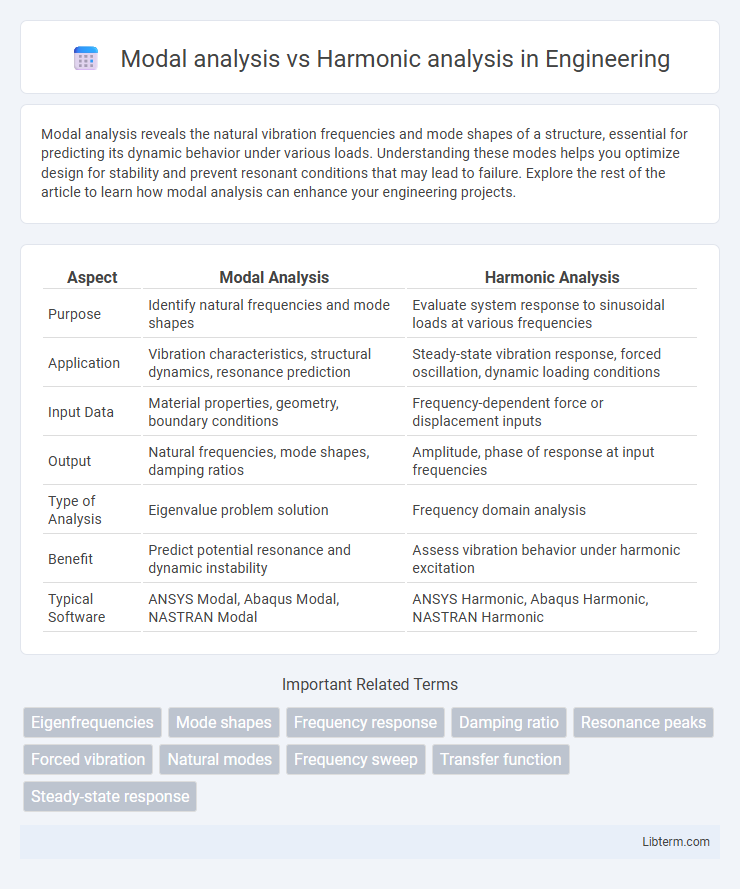
| Aspect | Modal Analysis | Harmonic Analysis |
|---|---|---|
| Purpose | Identify natural frequencies and mode shapes | Evaluate system response to sinusoidal loads at various frequencies |
| Application | Vibration characteristics, structural dynamics, resonance prediction | Steady-state vibration response, forced oscillation, dynamic loading conditions |
| Input Data | Material properties, geometry, boundary conditions | Frequency-dependent force or displacement inputs |
| Output | Natural frequencies, mode shapes, damping ratios | Amplitude, phase of response at input frequencies |
| Type of Analysis | Eigenvalue problem solution | Frequency domain analysis |
| Benefit | Predict potential resonance and dynamic instability | Assess vibration behavior under harmonic excitation |
| Typical Software | ANSYS Modal, Abaqus Modal, NASTRAN Modal | ANSYS Harmonic, Abaqus Harmonic, NASTRAN Harmonic |
Introduction to Modal and Harmonic Analysis
Modal analysis identifies natural frequencies and mode shapes of a structure to predict dynamic behavior under vibrational loads. Harmonic analysis evaluates steady-state response of a system to sinusoidal excitation at specific frequencies, revealing amplitude and phase information. Both techniques are essential for designing systems subjected to dynamic forces and optimizing structural integrity.
Fundamental Concepts: Modal Analysis Explained
Modal analysis identifies the natural vibration modes and natural frequencies of a structure by solving its eigenvalue problem, revealing how the structure deforms at each mode shape under free vibration conditions. Harmonic analysis, on the other hand, evaluates the steady-state response of a structure subjected to sinusoidal loads at various frequencies, focusing on amplitude and phase of vibrations. Understanding modal analysis is fundamental for predicting resonance and dynamic behavior, as it decomposes complex vibrations into a set of orthogonal mode shapes and corresponding natural frequencies.
Key Principles of Harmonic Analysis
Harmonic analysis focuses on determining the steady-state response of structures under sinusoidal loading by solving frequency domain equations to capture amplitude and phase behavior at various excitation frequencies. It involves calculating displacement, stress, and strain responses to harmonic loads, essential for predicting resonance and dynamic amplification effects. Unlike modal analysis, which identifies natural frequencies and mode shapes without external forces, harmonic analysis directly assesses system behavior under specific periodic forces.
Differences Between Modal and Harmonic Analysis
Modal analysis identifies natural frequencies, mode shapes, and damping ratios of structures by evaluating their dynamic properties without external forces, while harmonic analysis calculates the steady-state response of a structure subjected to sinusoidal loads at varying frequencies. Modal analysis is essential for understanding inherent vibration characteristics, whereas harmonic analysis predicts displacement, stress, and acceleration under specific harmonic excitations. The key difference lies in modal analysis being a free vibration study, whereas harmonic analysis deals with forced vibrations at defined frequencies.
Applications of Modal Analysis in Engineering
Modal analysis identifies natural frequencies, mode shapes, and damping characteristics of structures, essential for predicting dynamic behavior and avoiding resonance in mechanical and civil engineering designs. It is widely applied in aerospace for evaluating aircraft vibration, automotive industries for chassis and component durability, and civil engineering for assessing buildings and bridges under seismic or wind loading. This analysis enables engineers to optimize material usage, enhance structural integrity, and improve noise, vibration, and harshness (NVH) performance in engineered systems.
Applications of Harmonic Analysis in Real-World Scenarios
Harmonic analysis is crucial in predicting the steady-state response of structures subjected to sinusoidal loads, making it indispensable in fields like automotive engineering for analyzing vibrations in engines and suspension systems. It enables the design of HVAC systems by evaluating acoustic noise levels and optimizing sound insulation in building engineering. In aerospace, harmonic analysis assists in assessing the dynamic behavior of aircraft components under cyclic aerodynamic forces, ensuring safety and structural integrity.
Data Requirements for Modal vs Harmonic Analysis
Modal analysis requires input data such as the mass, stiffness, and damping properties of the structure to determine natural frequencies and mode shapes. Harmonic analysis demands frequency-dependent load data and system response characteristics to evaluate steady-state behavior under sinusoidal excitations. Accurate material properties and boundary conditions are critical for both analyses, but harmonic analysis specifically needs detailed excitation frequency profiles.
Advantages and Limitations of Modal Analysis
Modal analysis identifies natural frequencies, mode shapes, and damping ratios of a structure, providing critical insights for predicting resonance and dynamic behavior under various loading conditions. It is advantageous for simplifying complex vibration problems and designing for vibration control but is limited in analyzing steady-state response under harmonic excitation or nonlinear effects. Modal analysis assumes linearity and time-invariance, which restricts its accuracy when dealing with structures experiencing large deformations or non-proportional damping.
Pros and Cons of Harmonic Analysis
Harmonic analysis excels in evaluating steady-state response of structures under sinusoidal loading, providing detailed frequency response and resonance behavior crucial for vibration analysis. Its limitations include high computational cost and complexity when dealing with non-linear systems or transient responses, making it less versatile than modal analysis in such scenarios. Despite these drawbacks, harmonic analysis offers precise insight into amplitude and phase distribution across frequencies, essential for designing systems prone to cyclic loads.
Choosing the Right Analysis Method for Your Project
Modal analysis identifies natural frequencies and mode shapes crucial for understanding structural dynamics, while harmonic analysis evaluates a system's steady-state response to sinusoidal loads. Choosing the right method depends on project goals; use modal analysis to predict resonance and vibration characteristics, and harmonic analysis to assess frequency response under cyclic loading conditions. Projects requiring dynamic stability or fatigue assessment must integrate both analyses for comprehensive insights.
Modal analysis Infographic
 libterm.com
libterm.com