Compressible flow occurs when fluid density changes significantly due to pressure variations, often at high velocities close to or above the speed of sound. Understanding these density changes is crucial for designing efficient systems in aerospace, gas dynamics, and propulsion technologies. Explore the rest of the article to deepen your grasp of compressible flow fundamentals and applications.
Table of Comparison
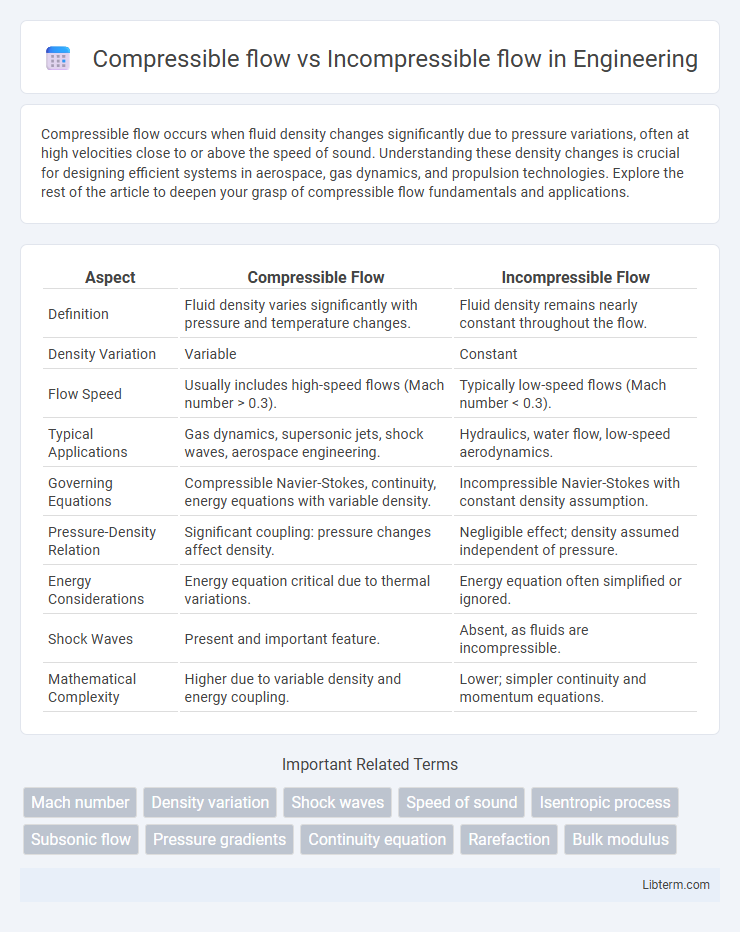
| Aspect | Compressible Flow | Incompressible Flow |
|---|---|---|
| Definition | Fluid density varies significantly with pressure and temperature changes. | Fluid density remains nearly constant throughout the flow. |
| Density Variation | Variable | Constant |
| Flow Speed | Usually includes high-speed flows (Mach number > 0.3). | Typically low-speed flows (Mach number < 0.3). |
| Typical Applications | Gas dynamics, supersonic jets, shock waves, aerospace engineering. | Hydraulics, water flow, low-speed aerodynamics. |
| Governing Equations | Compressible Navier-Stokes, continuity, energy equations with variable density. | Incompressible Navier-Stokes with constant density assumption. |
| Pressure-Density Relation | Significant coupling: pressure changes affect density. | Negligible effect; density assumed independent of pressure. |
| Energy Considerations | Energy equation critical due to thermal variations. | Energy equation often simplified or ignored. |
| Shock Waves | Present and important feature. | Absent, as fluids are incompressible. |
| Mathematical Complexity | Higher due to variable density and energy coupling. | Lower; simpler continuity and momentum equations. |
Introduction to Flow Dynamics
Compressible flow involves fluid density changes under varying pressure and temperature, commonly occurring in high-speed aerodynamics and gas dynamics. Incompressible flow assumes constant fluid density, often applicable to liquids and low-speed gas flow, simplifying the Navier-Stokes equations. Understanding the distinction between compressible and incompressible flow is crucial for accurately predicting pressure, velocity, and temperature fields in diverse engineering applications.
Defining Compressible Flow
Compressible flow occurs when fluid density varies significantly within the flow field, typically at Mach numbers greater than 0.3, causing changes in pressure, temperature, and volume. This type of flow is critical in high-speed aerodynamics, gas dynamics, and supersonic applications where shock waves and compressibility effects dominate. In contrast, incompressible flow assumes constant density, simplifying analysis for low-speed liquid flows and airflows with negligible density changes.
Defining Incompressible Flow
Incompressible flow is characterized by a constant fluid density throughout the flow field, typically applicable to liquids and low-speed gas flows where density variations are negligible. This assumption simplifies the continuity equation, allowing it to be expressed as the divergence of the velocity field equaling zero. Incompressible flow analysis is essential in hydraulics, aerodynamics at low Mach numbers (below 0.3), and many engineering applications where pressure changes do not significantly affect fluid density.
Key Differences Between Compressible and Incompressible Flow
Compressible flow involves significant changes in fluid density, typically occurring at high velocities close to or exceeding the speed of sound, while incompressible flow assumes constant density, common in low-speed fluid motion. Key differences include the presence of shock waves and variable pressure-density relationships in compressible flow, whereas incompressible flow follows simplified continuity and Bernoulli equations with constant density. Understanding these differences is crucial for accurate modeling in aerospace engineering, gas dynamics, and hydraulic systems design.
Governing Equations for Each Flow Type
Compressible flow governing equations include the full Navier-Stokes equations coupled with the continuity, momentum, and energy equations, accounting for density variations and compressibility effects through the compressible form of the conservation laws. Incompressible flow uses a simplified set of governing equations where density is constant, leading to the continuity equation reducing to a divergence-free velocity field, while the Navier-Stokes equations are solved without compressibility terms. The compressible flow equations require an equation of state, such as the ideal gas law, to relate pressure, temperature, and density, whereas incompressible flow assumes constant density and does not require this equation.
Applications of Compressible Flow
Compressible flow is essential in high-speed aerodynamics, gas turbines, and rocket propulsion where density changes significantly impact performance. Applications include supersonic aircraft design, nozzle flow in jet engines, and shock wave analysis in hypersonic vehicles. Understanding compressible flow enables optimization of engines, efficient fuel consumption, and accurate prediction of pressure and temperature variations in high-speed fluid dynamics.
Applications of Incompressible Flow
Incompressible flow is widely applied in hydraulic systems, water supply networks, and aerodynamic analysis of low-speed aircraft where density variations are negligible. It simplifies fluid dynamics equations, enabling efficient modeling of liquid pipelines, pump and turbine operations, and marine vessel hydrodynamics. Engineering designs for ventilation, HVAC systems, and blood flow simulations also predominantly utilize incompressible flow assumptions for accurate performance predictions.
Factors Affecting Flow Compressibility
Flow compressibility is primarily influenced by fluid velocity relative to the speed of sound, with Mach number values above 0.3 indicating significant compressibility effects. Fluid properties such as density, pressure, and temperature also affect compressibility, especially in gases where large pressure changes cause notable density variations. Moreover, fluid viscosity and flow geometry can alter local flow accelerations, impacting compressibility in practical aerodynamic and fluid dynamic applications.
Real-World Examples and Case Studies
Compressible flow occurs in high-speed aerodynamics such as supersonic jet engines and rocket nozzles, where density variations significantly influence pressure and temperature fields, exemplified by the shock waves around Concorde aircraft. Incompressible flow characterizes most low-speed fluid dynamics scenarios, including water flow in pipelines and air conditioning systems, where density changes are negligible, ensuring simplified analysis and design. Industrial case studies on gas turbine performance often require compressible flow modeling, while HVAC system optimization predominantly relies on incompressible flow assumptions.
Summary and Comparative Analysis
Compressible flow involves significant variations in fluid density, typically occurring at high velocities near or above Mach 0.3, whereas incompressible flow assumes constant density, common in low-speed fluid dynamics. Key differences include the influence of compressibility on pressure, temperature, and density changes in compressible flow, contrasted with negligible density variation and simpler continuity and momentum equations in incompressible flow. Understanding these distinctions is essential for accurate modeling in aerospace, hydraulics, and fluid machinery applications.
Compressible flow Infographic
 libterm.com
libterm.com