The Weber number is a dimensionless quantity used in fluid dynamics to describe the relative importance of inertial forces compared to surface tension forces in a fluid flow. It plays a crucial role in analyzing phenomena such as droplet formation, bubble dynamics, and multiphase flow behavior. Discover how understanding the Weber number can enhance your grasp of fluid mechanics in the rest of this article.
Table of Comparison
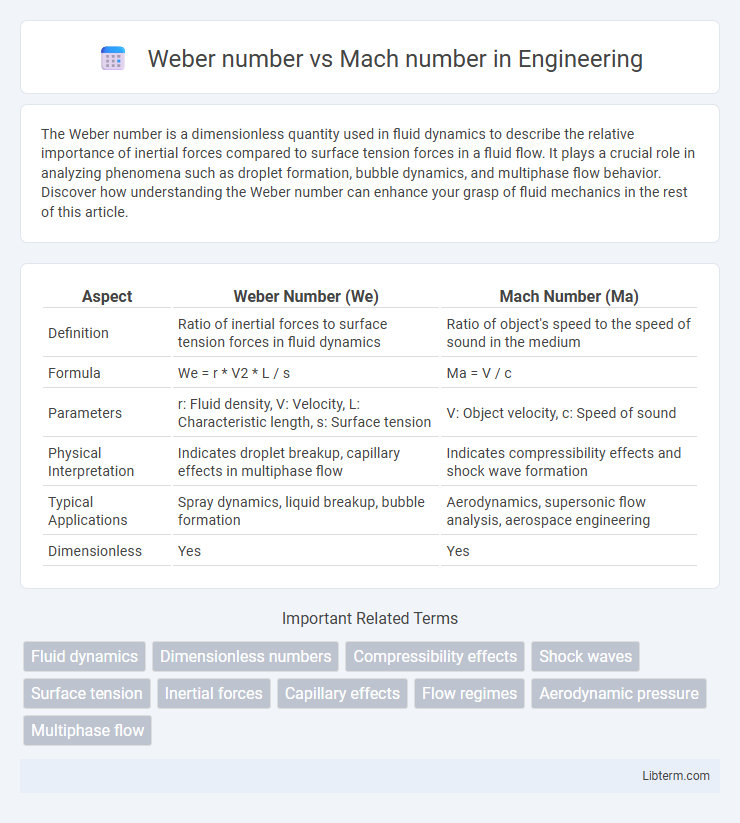
| Aspect | Weber Number (We) | Mach Number (Ma) |
|---|---|---|
| Definition | Ratio of inertial forces to surface tension forces in fluid dynamics | Ratio of object's speed to the speed of sound in the medium |
| Formula | We = r * V2 * L / s | Ma = V / c |
| Parameters | r: Fluid density, V: Velocity, L: Characteristic length, s: Surface tension | V: Object velocity, c: Speed of sound |
| Physical Interpretation | Indicates droplet breakup, capillary effects in multiphase flow | Indicates compressibility effects and shock wave formation |
| Typical Applications | Spray dynamics, liquid breakup, bubble formation | Aerodynamics, supersonic flow analysis, aerospace engineering |
| Dimensionless | Yes | Yes |
Introduction to Weber Number and Mach Number
The Weber number, a dimensionless quantity in fluid mechanics, measures the ratio of inertial forces to surface tension forces and is essential in analyzing droplet formation, bubble dynamics, and multiphase flows. The Mach number defines the ratio of an object's speed to the speed of sound in the surrounding medium, playing a crucial role in compressible flow phenomena and aerodynamics. Both numbers facilitate critical insights into fluid behavior under varying velocity and force conditions, influencing design and analysis in engineering applications.
Defining Weber Number: Fluid Dynamics Context
The Weber number (We) quantifies the relative importance of inertial forces to surface tension forces in fluid dynamics, particularly in multiphase flows involving droplets or bubbles. It is defined as We = ru2L/s, where r is fluid density, u is velocity, L is characteristic length, and s is surface tension coefficient. Unlike the Mach number, which measures compressibility effects by relating flow velocity to the speed of sound, the Weber number emphasizes the deformation and breakup of fluid interfaces under dynamic conditions.
Understanding Mach Number: Speed Relative to Sound
Mach number quantifies an object's speed relative to the speed of sound in a specific medium, crucial for analyzing supersonic and hypersonic flows. Understanding Mach number helps predict shock wave formation and compressibility effects in aerospace engineering and fluid dynamics. Unlike the Weber number, which assesses fluid inertia against surface tension in multiphase flows, the Mach number focuses on aerodynamic speed regimes and pressure wave behavior.
Mathematical Formulations: Weber vs Mach Number
The Weber number (We) is a dimensionless quantity expressed as \( We = \frac{\rho v^2 L}{\sigma} \), where \( \rho \) is fluid density, \( v \) is velocity, \( L \) is characteristic length, and \( \sigma \) is surface tension, quantifying the ratio of inertial forces to surface tension forces in fluid dynamics. The Mach number (Ma) is defined as \( Ma = \frac{v}{c} \), where \( v \) is flow velocity and \( c \) is the speed of sound in the medium, representing the ratio of flow velocity to acoustic wave speed. While the Weber number governs interface phenomena like droplet breakup, the Mach number governs compressibility and shock wave behavior in high-speed flows, making each crucial for different fluid dynamics regimes.
Key Physical Parameters Influencing Both Numbers
The Weber number quantifies the ratio of inertial forces to surface tension forces, primarily influenced by fluid density, characteristic velocity, droplet diameter, and surface tension coefficient. The Mach number represents the ratio of flow velocity to the speed of sound in the medium, depending critically on fluid velocity and speed of sound, which is governed by temperature, pressure, and gas composition. Both numbers are essential in fluid dynamics, where the Weber number dominates surface deformation phenomena and the Mach number dictates compressibility and shock wave interactions.
Applications of Weber Number in Engineering
The Weber number plays a crucial role in analyzing fluid dynamics where surface tension influences droplet formation, such as in spray coating, fuel injection, and inkjet printing technologies. It helps engineers design more efficient systems by predicting the breakup of liquid jets and droplets under various flow conditions. In contrast, the Mach number is primarily applied in high-speed aerodynamics to characterize compressible flows and shock wave behavior around aircraft and missiles.
Applications of Mach Number in Aerodynamics
Mach number, a critical dimensionless quantity in aerodynamics, quantifies the ratio of an object's speed to the speed of sound, influencing shock wave formation and airflow characteristics around aircraft. Applications of Mach number include supersonic and hypersonic flight design, where understanding compressibility effects and wave drag is essential for optimizing performance and stability. In comparison, the Weber number primarily addresses fluid dynamics involving surface tension effects, making Mach number more pertinent to aerodynamic analysis and aerospace engineering.
Differences Between Weber and Mach Number
The Weber number quantifies the ratio of inertial forces to surface tension forces in fluid flow, playing a crucial role in multiphase flows such as droplet formation and breakup. In contrast, the Mach number measures the ratio of an object's speed to the speed of sound, indicating compressibility effects in high-speed aerodynamics and gas dynamics. While the Weber number is dimensionless and primarily relevant to surface tension-dominated phenomena, the Mach number is essential for assessing compressibility and shock wave formation in supersonic flows.
Practical Examples Comparing the Two Numbers
The Weber number quantifies the relative importance of fluid inertia compared to surface tension, commonly used in analyzing droplet formation in inkjet printing where stable droplet breakup is crucial. The Mach number measures the ratio of flow velocity to the speed of sound, essential in aerospace engineering for determining shock wave formation around supersonic aircraft wings. Comparing these, Weber number is critical in microfluidic applications involving liquid sprays, while Mach number dominates scenarios involving compressible gas flows such as jet engine intake design.
Summary: Choosing the Right Dimensionless Number
The Weber number and Mach number serve distinct roles in fluid dynamics, with the Weber number emphasizing the ratio of inertial forces to surface tension in multiphase flows and the Mach number measuring flow velocity relative to the speed of sound, crucial for compressibility effects. Selecting the appropriate dimensionless number depends on the physical phenomena under investigation: interdroplet interactions and surface deformation require the Weber number, while supersonic flows and shock wave analysis necessitate the Mach number. Accurate modeling and scaling hinge on applying the dimensionless number that aligns with the dominant forces governing the fluid behavior.
Weber number Infographic
 libterm.com
libterm.com