Antiplane shear refers to a mode of deformation where displacement occurs perpendicular to the plane of interest, typically studied in material science and geophysics for understanding stress distribution and fracture mechanics. This type of shear is crucial for modeling seismic wave propagation and analyzing failure in layered materials. Explore the rest of the article to see how antiplane shear impacts various engineering and geophysical applications.
Table of Comparison
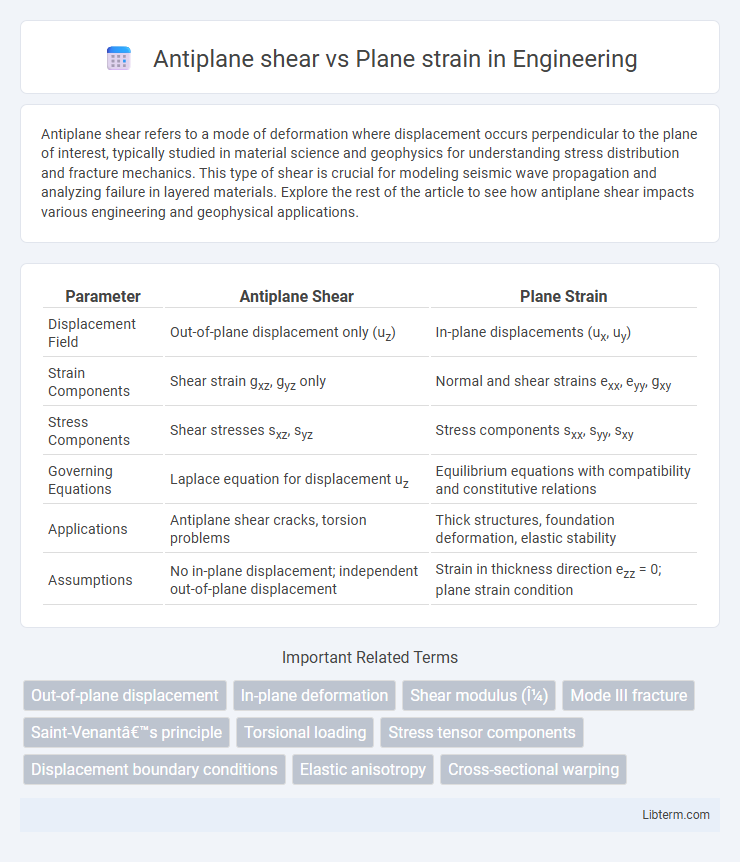
| Parameter | Antiplane Shear | Plane Strain |
|---|---|---|
| Displacement Field | Out-of-plane displacement only (uz) | In-plane displacements (ux, uy) |
| Strain Components | Shear strain gxz, gyz only | Normal and shear strains exx, eyy, gxy |
| Stress Components | Shear stresses sxz, syz | Stress components sxx, syy, sxy |
| Governing Equations | Laplace equation for displacement uz | Equilibrium equations with compatibility and constitutive relations |
| Applications | Antiplane shear cracks, torsion problems | Thick structures, foundation deformation, elastic stability |
| Assumptions | No in-plane displacement; independent out-of-plane displacement | Strain in thickness direction ezz = 0; plane strain condition |
Introduction to Antiplane Shear and Plane Strain
Antiplane shear refers to a deformation mode where displacement occurs perpendicular to the plane of interest, typically involving out-of-plane shear stresses without in-plane strains. Plane strain describes conditions where strain occurs only in two directions within a plane, while strain in the third direction is assumed zero, common in long structures subjected to load. Both concepts are fundamental in elasticity and fracture mechanics, helping to simplify complex three-dimensional stress states into two-dimensional analyses for materials such as metals, rocks, and polymers.
Fundamental Concepts and Definitions
Antiplane shear involves displacement occurring perpendicular to the plane of interest, typically characterized by out-of-plane shear stresses while in-plane normal stresses remain negligible. Plane strain assumes deformation in two dimensions with zero strain in the out-of-plane direction, leading to significant in-plane stresses and uniform strain along the thickness. Understanding these fundamental concepts is crucial for analyzing stress distribution and deformation patterns in materials under different loading conditions.
Mathematical Formulation
Antiplane shear deformation involves displacement occurring in the out-of-plane direction, where the displacement vector has only one non-zero component, typically \( u_z(x,y) \), governed by the scalar Laplace equation \( \nabla^2 u_z = 0 \). Plane strain assumes zero strain in the out-of-plane direction, leading to a two-dimensional problem with displacement components \( u_x(x,y) \) and \( u_y(x,y) \) satisfying equilibrium equations derived from Hooke's law under the plane strain condition \( \varepsilon_z = 0 \). The key mathematical distinction lies in antiplane shear reducing to a scalar equation for a single displacement component, while plane strain requires solving coupled partial differential equations for two in-plane displacement components with constitutive relations reflecting three-dimensional elasticity constraints.
Stress and Strain Components
Antiplane shear involves non-zero shear stress and strain components only in the out-of-plane direction, typically characterized by s_xz, s_yz, and g_xz, g_yz, with all in-plane normal stresses and strains being zero. Plane strain assumes zero strain in the out-of-plane direction (e_z = 0) and non-zero in-plane normal and shear stress components such as s_xx, s_yy, s_xy, with corresponding e_xx, e_yy, and g_xy strains. The key difference lies in antiplane shear's exclusive shear deformation out of the plane, contrasting with plane strain's deformation confinement within the plane and zero transverse strain.
Boundary Conditions Comparison
Antiplane shear involves displacement perpendicular to the plane, typically characterized by zero normal strain in the plane and stress components acting out-of-plane, with boundary conditions specifying shear traction or displacement in the out-of-plane direction. Plane strain assumes zero strain normal to the plane, resulting in in-plane displacements and stress components constrained within the plane, with boundary conditions applied to in-plane displacements or tractions. The key boundary condition difference lies in antiplane shear controlling out-of-plane displacement or shear stress, whereas plane strain controls in-plane displacements or normal and shear stresses.
Physical Interpretation and Applications
Antiplane shear involves displacement occurring perpendicular to the plane of interest, causing shear stress without volume change, commonly analyzed in torsion of circular shafts and seismic wave propagation. Plane strain assumes no strain in the thickness direction, idealizing extensive structures like dams and tunnels where deformation is constrained to two dimensions, reflecting stress distribution and material behavior under load. These distinctions guide engineers in selecting appropriate models for stress analysis based on geometry and boundary conditions in structural and geotechnical applications.
Key Differences Between Antiplane Shear and Plane Strain
Antiplane shear involves displacement occurring perpendicular to the plane of interest, typically characterized by out-of-plane shear stresses without normal strains, whereas plane strain assumes deformation confined within a plane with zero strain in the thickness direction, leading to in-plane normal and shear stresses. The mathematical formulation for antiplane shear reduces to a scalar displacement field governed by Laplace's equation, contrasting with plane strain which requires solving coupled partial differential equations in two dimensions. Applications in geotechnical engineering highlight antiplane shear for modeling out-of-plane slip surfaces, while plane strain is favored for analyzing stress and deformation in long structures where thickness effects are negligible.
Typical Problems and Examples
Antiplane shear problems typically involve out-of-plane shear deformation where displacements occur perpendicular to the plane, common in fracture mechanics and shear wave propagation analyses. Plane strain problems describe in-plane deformation with negligible strain in the thickness direction, frequently applied in geotechnical engineering, tunnel stability, and thick-walled pressure vessel design. Both formulations address different boundary conditions and displacement constraints, influencing stress distribution and material response in elasticity and plasticity studies.
Advantages and Limitations
Antiplane shear deformation simplifies three-dimensional elasticity problems by restricting displacement to a single out-of-plane direction, allowing exact analytical solutions and efficient numerical modeling, which is advantageous for fracture mechanics and wave propagation analysis. Plane strain assumes zero strain in the out-of-plane direction, representing thick structures under in-plane loads, providing accurate stress prediction in components like dams or tunnels but limited to geometries where thickness effects dominate. Antiplane shear's limitation lies in its reduced applicability to real-world 3D stress states, while plane strain cannot capture out-of-plane displacements, limiting its use in thin or flexible structures.
Summary and Practical Implications
Antiplane shear involves displacement perpendicular to the plane of interest with no in-plane strain, ideal for modeling out-of-plane shear stress scenarios in materials like fault zones or layered composites. Plane strain assumes zero strain in the thickness direction, useful for analyzing thick structures like dams or tunnels where deformation primarily occurs in the plane. Understanding these differences helps engineers choose appropriate models for stress analysis, ensuring accurate predictions of material behavior under various loading conditions.
Antiplane shear Infographic
 libterm.com
libterm.com