Bode plots graphically represent a system's frequency response through magnitude and phase angle across frequencies, crucial for analyzing stability and performance in control systems. Understanding your system's Bode plot helps you identify gain margins, phase margins, and bandwidth, enabling better design and tuning decisions. Explore the full article to deepen your knowledge and enhance your control system analysis skills.
Table of Comparison
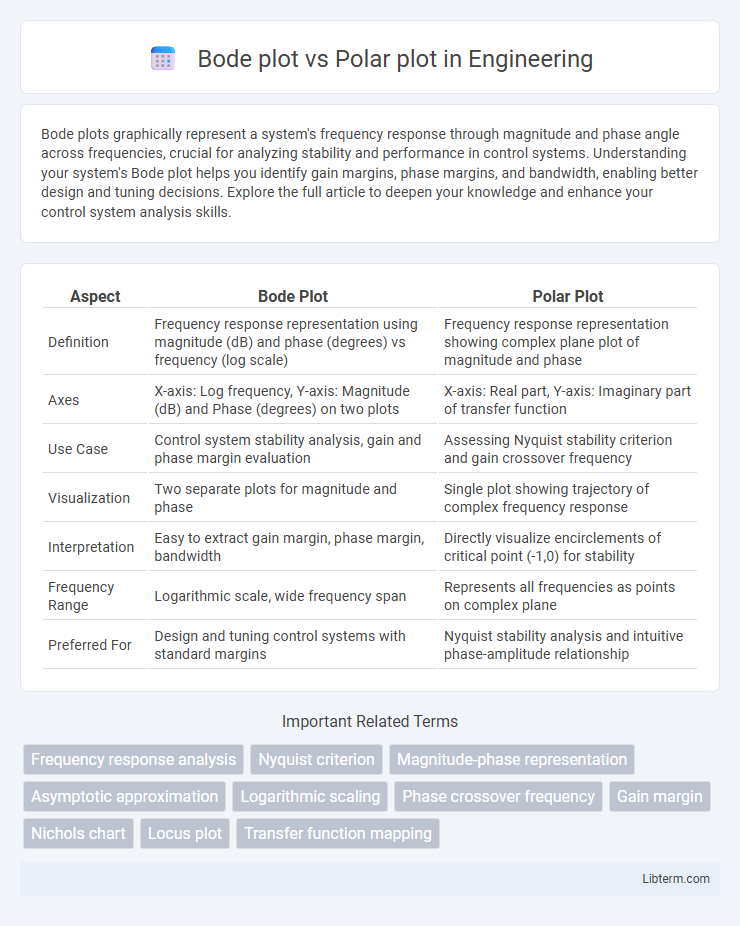
| Aspect | Bode Plot | Polar Plot |
|---|---|---|
| Definition | Frequency response representation using magnitude (dB) and phase (degrees) vs frequency (log scale) | Frequency response representation showing complex plane plot of magnitude and phase |
| Axes | X-axis: Log frequency, Y-axis: Magnitude (dB) and Phase (degrees) on two plots | X-axis: Real part, Y-axis: Imaginary part of transfer function |
| Use Case | Control system stability analysis, gain and phase margin evaluation | Assessing Nyquist stability criterion and gain crossover frequency |
| Visualization | Two separate plots for magnitude and phase | Single plot showing trajectory of complex frequency response |
| Interpretation | Easy to extract gain margin, phase margin, bandwidth | Directly visualize encirclements of critical point (-1,0) for stability |
| Frequency Range | Logarithmic scale, wide frequency span | Represents all frequencies as points on complex plane |
| Preferred For | Design and tuning control systems with standard margins | Nyquist stability analysis and intuitive phase-amplitude relationship |
Introduction to Bode and Polar Plots
Bode plots represent frequency response through separate magnitude and phase graphs plotted against logarithmic frequency scales, making them essential for analyzing and designing control systems and filters. Polar plots depict complex frequency response by mapping magnitude and phase as a single curve in the complex plane, offering intuitive visualization of stability margins and resonance characteristics. Both plots are fundamental in electrical engineering for understanding system behavior but emphasize different aspects of frequency domain analysis.
Definition of Bode Plot
A Bode plot is a graphical representation of a linear, time-invariant system's frequency response, consisting of two plots: magnitude (in decibels) versus frequency and phase angle versus frequency, both on logarithmic scales. It is primarily used to analyze the gain and phase behavior of control systems and filters across a range of frequencies. Unlike polar plots, which map complex frequency response directly onto the complex plane, Bode plots separate magnitude and phase for clearer visualization and ease of stability analysis.
Definition of Polar Plot
A polar plot graphically represents the complex frequency response of a system by plotting the magnitude and phase of a transfer function on a polar coordinate plane, where the radius corresponds to magnitude and the angle corresponds to phase. Unlike a Bode plot, which displays magnitude and phase separately against frequency on Cartesian axes, the polar plot combines both into a single continuous curve, offering direct visualization of stability margins and resonance behavior. This representation is particularly useful for assessing gain and phase margins in control systems by examining how the plot encircles or approaches the critical point (-1,0).
Key Differences Between Bode and Polar Plots
Bode plots show gain and phase versus frequency on separate logarithmic scales, making it easier to analyze system stability and frequency response in control systems. Polar plots, in contrast, represent complex frequency response as a single curve in the complex plane, offering a visual correlation between magnitude and phase simultaneously. Key differences include Bode plots' use of decibels and degrees on linear graphs, while polar plots use magnitude and phase as radius and angle in a circular format.
Use Cases: When to Use Bode Plot
Bode plots excel in control system analysis, specifically for assessing system stability, gain margin, and phase margin across frequency ranges. They are preferred when designing feedback controllers or tuning compensators to ensure desired transient response and steady-state accuracy. Use Bode plots to visualize frequency response in linear, time-invariant systems, especially in electrical and mechanical engineering applications.
Use Cases: When to Use Polar Plot
Polar plots excel in representing frequency response of systems with a focus on phase and gain margins, making them ideal for assessing system stability and robustness in control engineering. They provide a clear visualization of how the complex frequency response encircles the critical point (-1,0), which is crucial for Nyquist stability criteria analysis. Use polar plots when detailed inspection of frequency-dependent phase shifts and potential encirclements of critical points is necessary, especially in feedback control system design and stability evaluation.
Advantages of Bode Plot
Bode plots offer a clear representation of system frequency response by separately illustrating magnitude and phase over a logarithmic frequency scale, which simplifies analysis and design of control systems. The logarithmic scale enhances the visibility of system behavior across a wide frequency range, making it easier to identify gain margins, phase margins, and bandwidth. These features provide engineers with intuitive insight into stability and performance, facilitating efficient system tuning compared to the more complex visual interpretation required by polar plots.
Advantages of Polar Plot
Polar plots offer a comprehensive visualization of system frequency response by simultaneously displaying magnitude and phase information on a single graph, enhancing the clarity of stability and resonance characteristics. They enable straightforward identification of gain and phase margins, critical for control system design and analysis, which can be cumbersome with separate Bode plots. The continuous representation of complex impedance or transfer function vectors in polar plots provides intuitive insight into system behavior, particularly for oscillatory and feedback systems.
Limitations of Bode and Polar Plots
Bode plots are limited in representing systems with non-minimum phase characteristics or those exhibiting strong nonlinearities, as they display magnitude and phase separately over frequency, potentially obscuring phase-magnitude relationships. Polar plots, while illustrating the frequency response in a combined magnitude-phase form, can become cluttered and difficult to interpret for high-order systems due to overlapping trajectories. Both plots face challenges in accurately depicting complex dynamics like time delays or non-linear responses, limiting their standalone diagnostic effectiveness.
Comparative Summary: Bode Plot vs Polar Plot
Bode plots graph frequency response using separate magnitude and phase logarithmic plots, ideal for analyzing linear time-invariant systems' gain and phase margins. Polar plots represent frequency response on a complex plane, illustrating amplitude and phase simultaneously, beneficial for visualizing system stability and Nyquist criteria. Bode plots offer clearer numerical interpretation, while polar plots provide intuitive geometric insights into system behavior and stability margins.
Bode plot Infographic
 libterm.com
libterm.com