Turbulent flow is characterized by chaotic, irregular fluid motion that significantly enhances mixing and momentum transfer compared to laminar flow. This complex behavior occurs at high velocities or with fluids of low viscosity, making it crucial in engineering applications such as pipeline design and aerodynamic analysis. Discover how understanding turbulent flow can improve your approach to fluid dynamics by exploring the full article.
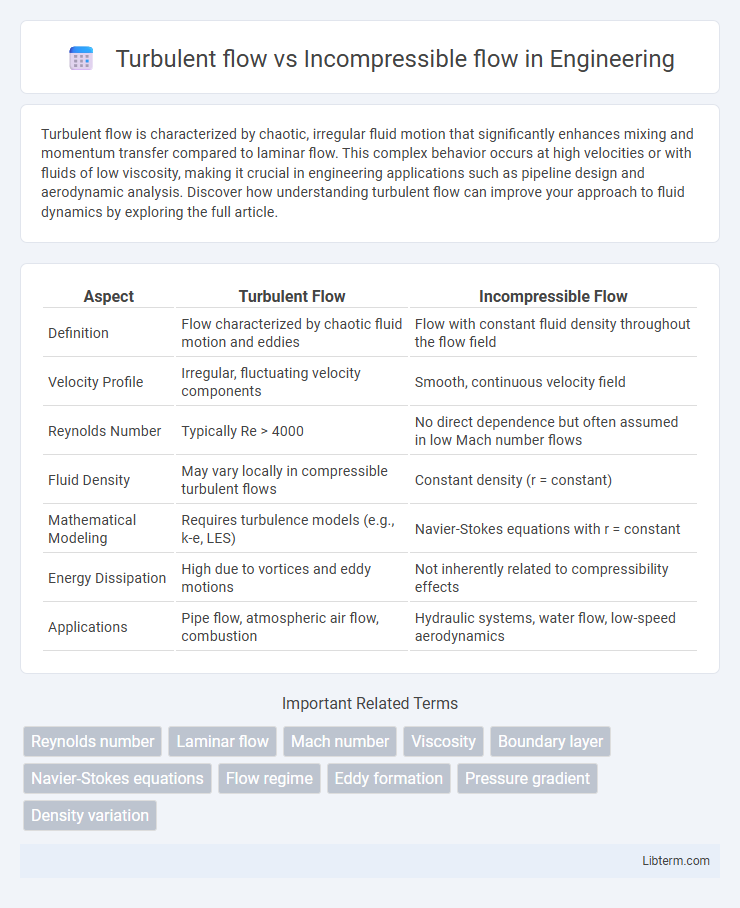
Table of Comparison
| Aspect | Turbulent Flow | Incompressible Flow |
|---|---|---|
| Definition | Flow characterized by chaotic fluid motion and eddies | Flow with constant fluid density throughout the flow field |
| Velocity Profile | Irregular, fluctuating velocity components | Smooth, continuous velocity field |
| Reynolds Number | Typically Re > 4000 | No direct dependence but often assumed in low Mach number flows |
| Fluid Density | May vary locally in compressible turbulent flows | Constant density (r = constant) |
| Mathematical Modeling | Requires turbulence models (e.g., k-e, LES) | Navier-Stokes equations with r = constant |
| Energy Dissipation | High due to vortices and eddy motions | Not inherently related to compressibility effects |
| Applications | Pipe flow, atmospheric air flow, combustion | Hydraulic systems, water flow, low-speed aerodynamics |
Understanding Turbulent Flow
Turbulent flow is characterized by chaotic, irregular fluid motion with eddies and vortices, significantly increasing momentum and heat transfer rates compared to laminar flow. Unlike incompressible flow, which assumes constant fluid density, turbulent flow can occur in both compressible and incompressible fluids but is distinguished by high Reynolds numbers typically above 4000. Understanding turbulent flow is crucial for accurately predicting fluid dynamics in engineering applications such as aerodynamics, pipeline transport, and atmospheric science.
Defining Incompressible Flow
Incompressible flow is characterized by a constant fluid density throughout the flow field, meaning the divergence of the velocity vector is zero, ensuring volume conservation. This type of flow is commonly assumed in liquids and low-speed gas flows where density variations are negligible. Turbulent flow, by contrast, refers to chaotic and irregular fluid motion with eddies and vortices, which can occur in both compressible and incompressible regimes depending on flow conditions like Reynolds number.
Key Differences Between Turbulent and Incompressible Flow
Turbulent flow is characterized by chaotic and irregular fluid motion with significant mixing and fluctuations in velocity, whereas incompressible flow assumes constant fluid density regardless of pressure changes. Turbulence involves nonlinear and unpredictable velocity variations, while incompressible flow applies primarily to fluids with negligible density changes, often simplifying the Navier-Stokes equations. The key difference lies in flow behavior: turbulence describes flow regime complexity, and incompressibility relates to fluid density properties under flow conditions.
Fundamental Principles of Turbulent Flow
Turbulent flow is characterized by chaotic fluid motion with eddies, vortices, and rapid fluctuations in velocity and pressure, unlike incompressible flow, which assumes constant fluid density and steady velocity fields. The fundamental principles of turbulent flow include the Reynolds decomposition, which separates flow variables into mean and fluctuating components, and the Reynolds-averaged Navier-Stokes (RANS) equations that describe averaged turbulent behavior. Energy cascades from larger to smaller scales in turbulent flows, with viscous dissipation occurring at the smallest scales, ensuring momentum and energy transport far exceed those in laminar or incompressible flows.
Core Characteristics of Incompressible Flow
Incompressible flow is characterized by a constant fluid density throughout the flow field, often modeled under the assumption that density variations are negligible. The core features include a divergence-free velocity field, expressed mathematically as *u = 0, ensuring mass conservation without volumetric expansion or compression. Unlike turbulent flow, incompressible flow can be either laminar or turbulent, but the defining trait remains the preservation of density, which simplifies the Navier-Stokes equations and influences pressure and velocity distributions.
Factors Influencing Flow Regimes
Turbulent flow occurs when inertial forces dominate viscous forces, typically at high Reynolds numbers above 4000, causing chaotic fluid motion characterized by eddies and vortices. Incompressible flow assumes constant fluid density, primarily influenced by fluid velocity, viscosity, and pipe roughness but neglects density changes that affect compressible regimes. Flow regimes are driven by factors such as fluid velocity, characteristic length scale, viscosity, and surface roughness, which determine whether the flow remains laminar, transitions to turbulent, or maintains incompressibility.
Real-World Applications of Turbulent Flow
Turbulent flow occurs when fluid motion is characterized by chaotic changes in pressure and velocity, commonly seen in aerodynamics, pipeline transport, and atmospheric dynamics, enhancing mixing and heat transfer efficiency. Incompressible flow assumes constant fluid density, ideal for simulating liquid behaviors in hydraulic systems and low-speed airflows where density variations are negligible. Real-world applications of turbulent flow include efficient combustion in engines, improved chemical reactor performance, and pollutant dispersion modeling in environmental engineering.
Engineering Relevance of Incompressible Flow
Incompressible flow, characterized by constant fluid density, is crucial in engineering applications involving liquids and low-speed gases where density variations are negligible. This assumption simplifies fluid dynamics equations, enabling accurate analysis and design of pumps, pipelines, and hydraulic systems. Turbulent flow often occurs in these systems, but treating the flow as incompressible allows engineers to apply Reynolds-averaged Navier-Stokes equations and turbulence models effectively for reliable performance predictions.
Experimental Techniques for Flow Analysis
Experimental techniques for analyzing turbulent flow commonly include Particle Image Velocimetry (PIV) and Laser Doppler Anemometry (LDA), which provide high-resolution velocity field measurements and capture chaotic fluctuations characteristic of turbulence. In contrast, incompressible flow experiments often utilize hot-wire anemometry and dye injection methods to visualize and quantify steady velocity profiles and streamline patterns. Both approaches rely on advanced sensors and data acquisition systems tailored to capture the distinct dynamic properties of each flow regime.
Comparative Summary: Turbulent vs Incompressible Flow
Turbulent flow is characterized by chaotic fluid motion with irregular fluctuations and high momentum diffusion, commonly occurring at high Reynolds numbers, whereas incompressible flow assumes constant fluid density throughout the motion, simplifying the continuity equation. Turbulent flow involves complex velocity fields and eddies, leading to enhanced mixing and increased energy dissipation, while incompressible flow can be either laminar or turbulent but primarily focuses on density invariance without compressibility effects. The key distinction lies in turbulence involving fluid velocity randomness and momentum transport, whereas incompressibility pertains strictly to density constancy, impacting the mathematical modeling and computational fluid dynamics simulations.
Turbulent flow Infographic
 libterm.com
libterm.com