The root circle represents the boundary on a gear where the teeth are cut to their deepest point, crucial for ensuring proper meshing and strength. Understanding the root circle helps optimize gear performance by minimizing stress concentrations and wear. Discover how mastering the root circle concept can improve your mechanical designs by reading the full article.
Table of Comparison
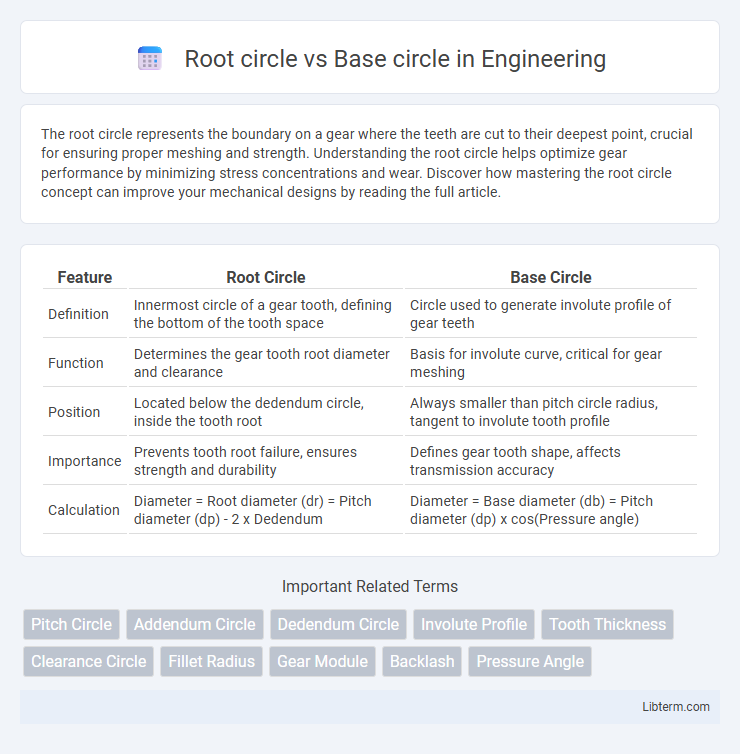
| Feature | Root Circle | Base Circle |
|---|---|---|
| Definition | Innermost circle of a gear tooth, defining the bottom of the tooth space | Circle used to generate involute profile of gear teeth |
| Function | Determines the gear tooth root diameter and clearance | Basis for involute curve, critical for gear meshing |
| Position | Located below the dedendum circle, inside the tooth root | Always smaller than pitch circle radius, tangent to involute tooth profile |
| Importance | Prevents tooth root failure, ensures strength and durability | Defines gear tooth shape, affects transmission accuracy |
| Calculation | Diameter = Root diameter (dr) = Pitch diameter (dp) - 2 x Dedendum | Diameter = Base diameter (db) = Pitch diameter (dp) x cos(Pressure angle) |
Understanding Root Circle and Base Circle
The root circle represents the smallest diameter of a gear, marking the bottom of the tooth spaces, while the base circle is fundamental in defining the involute profile of the gear teeth and lies below the pitch circle. Understanding the root circle is crucial for determining gear tooth strength and avoiding interference, whereas the base circle serves as the circle from which the involute curve is generated, directly influencing the gear's transmission and engagement quality. Accurate knowledge of both circles ensures proper gear design, durability, and efficient power transmission in mechanical systems.
Definitions of Root Circle and Base Circle
The root circle defines the innermost boundary of a gear tooth where the tooth thickness tapers and the root fillet begins, crucial for determining the gear's strength and durability. The base circle serves as the foundational reference from which the involute tooth profile is generated, impacting the gear's pressure angle and smooth meshing. Understanding the distinct roles of the root circle and base circle is essential for precise gear design and performance optimization.
Key Differences Between Root Circle and Base Circle
The root circle defines the innermost boundary of a gear tooth, representing the bottom of the tooth space, while the base circle is the circle from which the involute tooth profile is generated, crucial for defining the gear's geometry and motion. The root circle diameter is smaller than the base circle diameter and impacts the gear's strength and clearance, whereas the base circle diameter influences the pitch and pressure angle of the gear teeth. Understanding these differences is essential for gear design accuracy, affecting load distribution and manufacturing precision.
Importance in Gear Design
The root circle defines the bottom diameter of the gear tooth space, crucial for determining the gear tooth's strength and clearance, while the base circle is fundamental for generating the involute profile that ensures smooth transmission of motion. Accurate dimensioning of the root circle prevents undercutting and gear tooth failure, whereas the base circle radius directly influences the pressure angle and gear mesh efficiency. Understanding the relationship between these circles optimizes gear durability, load distribution, and performance in mechanical systems.
Mathematical Formulas for Root and Base Circles
The root circle diameter \( d_r \) in gear geometry is calculated as \( d_r = d - 2 \times h_a - 2 \times h_f \), where \( d \) is the pitch diameter, \( h_a \) is the addendum, and \( h_f \) is the dedendum. The base circle diameter \( d_b \) is derived from the pitch circle diameter \( d \) using the formula \( d_b = d \times \cos(\phi) \), where \( \phi \) is the pressure angle. Precise determination of these circles is critical for gear tooth profile generation and gear meshing analysis.
Practical Applications in Engineering
The base circle serves as the fundamental reference for involute gear tooth profiles, crucial in precision gear design and analysis. The root circle defines the gear's tooth root, impacting strength and wear resistance in mechanical power transmission. Practical engineering applications leverage the base circle for calculating contact ratios, while the root circle aids in determining gear durability under load conditions.
Influence on Gear Strength and Performance
The root circle defines the minimum diameter of a gear tooth, directly affecting gear strength by determining the thickness of the tooth base and resistance to bending stress. The base circle is critical for generating the involute tooth profile, influencing gear performance through accurate transmission of motion and load distribution. A smaller root circle increases tooth strength but may reduce contact ratio, while the base circle ensures smooth meshing and efficient power transfer.
Common Misconceptions and Errors
Many engineers confuse the root circle with the base circle, incorrectly assuming both define the same gear profile limits. The root circle represents the bottom of the gear tooth space, crucial for clearance and strength, while the base circle is the foundation for the involute tooth profile and influences gear motion. Misinterpreting these distinct circles leads to errors in gear design, affecting meshing accuracy and operational efficiency.
Visual Representation: Diagrams and Comparisons
The root circle and base circle are fundamental concepts in gear geometry, distinctly represented in diagrams where the root circle defines the innermost boundary of the gear teeth, and the base circle serves as the foundation for involute tooth profiles. Visual representations typically show the root circle as a smaller, inner circle touching the bottom of the tooth spaces, while the base circle lies between the pitch circle and root circle, crucial for generating the involute curve that ensures smooth gear meshing. Comparing diagrams highlights the spatial relationship and size difference, clarifying how the base circle radius influences the involute profile and the root circle ensures sufficient tooth strength and clearance.
Selecting the Right Circle for Gear Calculations
Selecting the right circle for gear calculations depends on the specific aspect being analyzed: the root circle represents the bottom of the gear tooth space, critical for determining gear tooth strength and clearance, while the base circle is fundamental for defining the involute profile and calculating the gear's pitch and velocity ratio. Accurate gear design requires using the base circle for involute geometry calculations to ensure proper meshing and smooth transmission of motion. Engineers prioritize the root circle when assessing undercutting risks and tooth durability during load and stress evaluations.
Root circle Infographic
 libterm.com
libterm.com