Young's modulus measures a material's stiffness by quantifying the relationship between stress and strain in its elastic region. It is a critical parameter for engineers and designers when selecting materials for construction, machinery, or product development to ensure structural integrity and performance. Explore the article to understand how Young's modulus influences material behavior and applications.
Table of Comparison
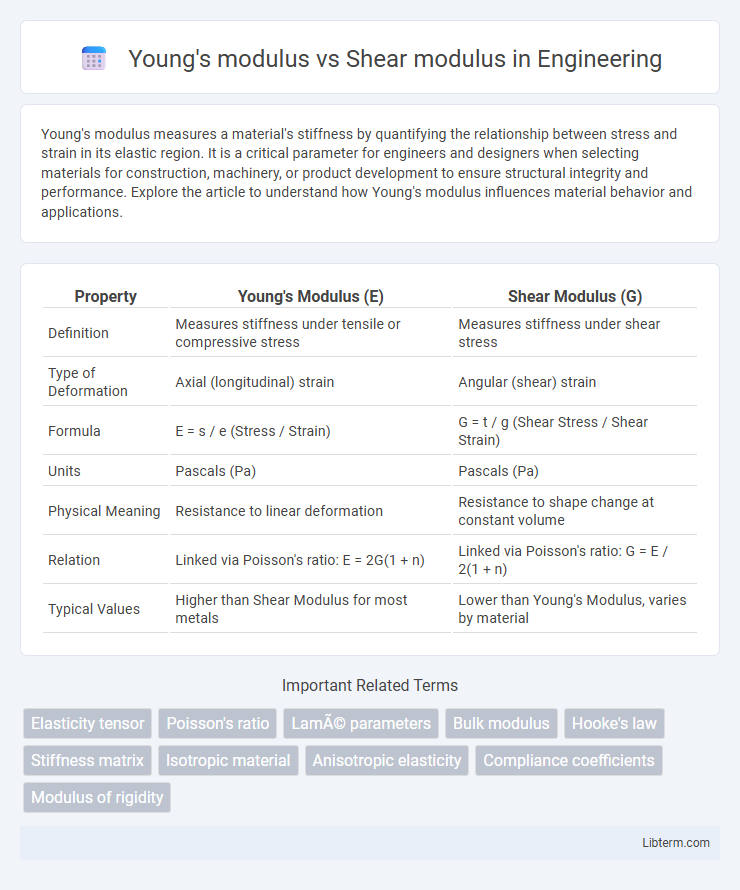
| Property | Young's Modulus (E) | Shear Modulus (G) |
|---|---|---|
| Definition | Measures stiffness under tensile or compressive stress | Measures stiffness under shear stress |
| Type of Deformation | Axial (longitudinal) strain | Angular (shear) strain |
| Formula | E = s / e (Stress / Strain) | G = t / g (Shear Stress / Shear Strain) |
| Units | Pascals (Pa) | Pascals (Pa) |
| Physical Meaning | Resistance to linear deformation | Resistance to shape change at constant volume |
| Relation | Linked via Poisson's ratio: E = 2G(1 + n) | Linked via Poisson's ratio: G = E / 2(1 + n) |
| Typical Values | Higher than Shear Modulus for most metals | Lower than Young's Modulus, varies by material |
Introduction to Young's Modulus and Shear Modulus
Young's modulus measures a material's ability to resist linear deformation under tensile stress, reflecting stiffness in stretching or compressing along one axis. Shear modulus quantifies resistance to shape changes caused by shear stress, indicating how a material resists sliding layers. Both moduli are fundamental elastic constants critical for engineering applications involving deformation analysis.
Fundamental Definitions and Concepts
Young's modulus measures a material's ability to resist uniaxial tensile stress, quantifying stiffness in linear stretching or compression. Shear modulus defines a material's response to shear stress, assessing resistance to shape changes without volume alteration. Both moduli are fundamental elastic constants linked through Poisson's ratio and describe distinct deformation modes critical in mechanical and structural analysis.
Differences Between Young’s Modulus and Shear Modulus
Young's modulus measures a material's ability to resist axial deformation under tensile or compressive forces, quantified by the ratio of normal stress to axial strain. Shear modulus, also known as modulus of rigidity, quantifies a material's response to shear stress, defined as the ratio of shear stress to shear strain. The key difference lies in the type of deformation: Young's modulus relates to linear stretching or compression, while shear modulus pertains to angular distortion or shape changes without volume alteration.
Mathematical Formulations and Units
Young's modulus (E) is defined mathematically as the ratio of tensile stress to tensile strain, expressed as E = s/e, where s is stress in pascals (Pa) and e is the dimensionless strain. Shear modulus (G), also known as the modulus of rigidity, is formulated as G = t/g, representing the ratio of shear stress (t) to shear strain (g), with t measured in pascals and g as a dimensionless quantity. Both moduli share the unit of pascals (Pa) but quantify different types of deformation responses in materials under linear elastic conditions.
Physical Significance in Material Science
Young's modulus measures a material's ability to resist axial deformation under tensile or compressive stress, reflecting stiffness along the applied load direction. Shear modulus quantifies resistance to shape changes under shear stress, indicating how a material deforms tangentially. Both moduli are fundamental in characterizing elastic behavior, with Young's modulus linked to longitudinal strain and shear modulus related to angular distortion in materials.
Young’s Modulus: Applications and Examples
Young's modulus, a fundamental mechanical property, measures a material's stiffness under tensile stress and is crucial in structural engineering for designing bridges, buildings, and aircraft components. It helps predict how much a material will elastically deform when subjected to axial loads, ensuring safety and durability in construction. Applications include selecting materials like steel, aluminum, and composites where resistance to elongation directly impacts performance and reliability.
Shear Modulus: Applications and Examples
Shear modulus, also known as modulus of rigidity, quantifies a material's resistance to shear deformation and plays a critical role in engineering applications involving torsion and shear forces. It is essential for designing components like shafts, beams, and fasteners where shear stress influences performance and safety. Common examples include steel drive shafts in automotive engineering, where shear modulus ensures efficient torque transmission without excessive deformation.
Relationship Between Young’s Modulus, Shear Modulus, and Poisson’s Ratio
Young's modulus (E) and shear modulus (G) are fundamental mechanical properties describing a material's elasticity under tensile and shear stress, respectively. Their relationship is mathematically expressed as E = 2G(1 + n), where n is Poisson's ratio, highlighting the interdependence between normal and shear deformation characteristics. Knowing any two of these parameters allows for the determination of the third, essential for material characterization and engineering design.
Factors Affecting Young’s and Shear Moduli
Material composition, temperature, and microstructural defects significantly influence Young's modulus and shear modulus by altering atomic bonding strength and lattice arrangements. Crystallographic orientation and phase distribution within alloys also impact elastic moduli, with anisotropic materials showing variance in modulus values depending on load direction. Environmental factors such as humidity and strain rate further affect these moduli by changing deformation mechanisms at the microscopic scale.
Summary Table: Young’s Modulus vs Shear Modulus
Young's modulus measures a material's stiffness under tensile or compressive stress, indicating how much it stretches or compresses, typically expressed in pascals (Pa). Shear modulus quantifies a material's response to shear stress, reflecting its ability to resist shape changes without volume alteration, also measured in pascals. The summary table highlights these differences: Young's modulus governs longitudinal deformation, shear modulus governs angular deformation, and their ratio defines Poisson's ratio for isotropic materials.
Young's modulus Infographic
 libterm.com
libterm.com