Axisymmetric structures or phenomena exhibit symmetry around a central axis, meaning their properties remain consistent when rotated about this axis. This concept plays a crucial role in fields like fluid dynamics, mechanical engineering, and physics, where simplifying complex systems into axisymmetric models allows for easier analysis and design. Explore the rest of the article to understand how axisymmetric principles impact various applications and your projects.
Table of Comparison
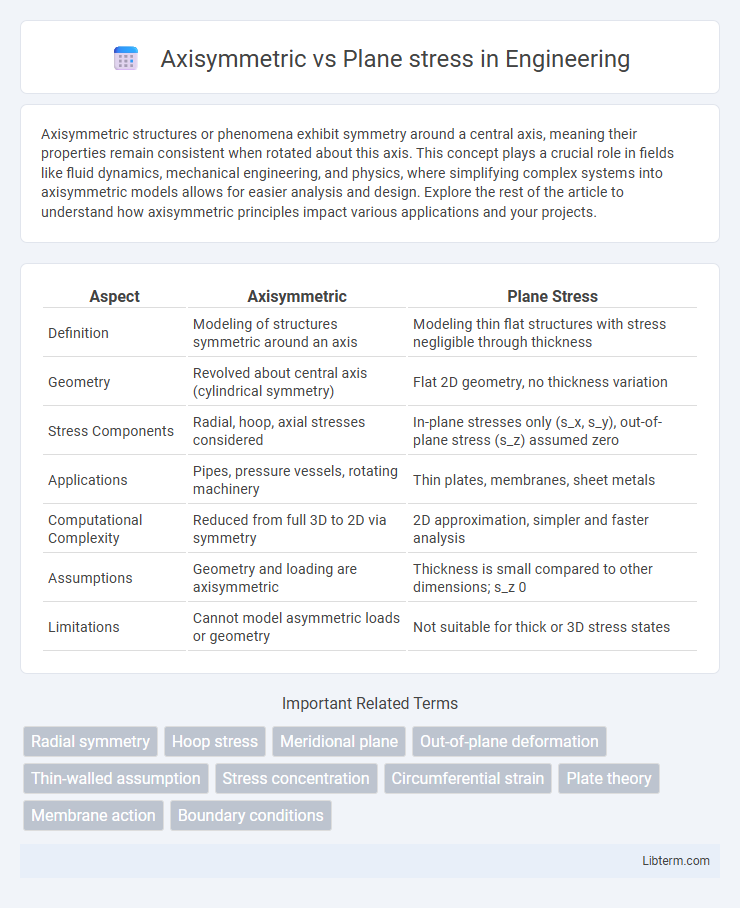
| Aspect | Axisymmetric | Plane Stress |
|---|---|---|
| Definition | Modeling of structures symmetric around an axis | Modeling thin flat structures with stress negligible through thickness |
| Geometry | Revolved about central axis (cylindrical symmetry) | Flat 2D geometry, no thickness variation |
| Stress Components | Radial, hoop, axial stresses considered | In-plane stresses only (s_x, s_y), out-of-plane stress (s_z) assumed zero |
| Applications | Pipes, pressure vessels, rotating machinery | Thin plates, membranes, sheet metals |
| Computational Complexity | Reduced from full 3D to 2D via symmetry | 2D approximation, simpler and faster analysis |
| Assumptions | Geometry and loading are axisymmetric | Thickness is small compared to other dimensions; s_z 0 |
| Limitations | Cannot model asymmetric loads or geometry | Not suitable for thick or 3D stress states |
Introduction to Axisymmetric and Plane Stress
Axisymmetric analysis involves structures or components subjected to loads and boundary conditions symmetric about an axis, simplifying 3D problems into 2D by assuming uniformity around the axis. Plane stress describes thin structures where stress in the thickness direction is negligible, reducing the state of stress to two dimensions, mainly in thin plates or shells. Both methods optimize computational resources by leveraging geometric and loading symmetries to analyze mechanical behavior efficiently.
Fundamental Concepts and Definitions
Axisymmetric stress analysis addresses structures subjected to loads symmetric about an axis, simplifying three-dimensional problems into two dimensions by assuming uniformity around the axis, which is essential for cylindrical or rotationally symmetric components. Plane stress conditions apply to thin plates where out-of-plane stresses (s_z) are negligible, allowing stress analysis confined to the plane (s_x, s_y, t_xy), critical for thin-walled structures under in-plane loading. Understanding these fundamental distinctions aids in selecting appropriate modeling approaches for accurate stress-strain predictions in mechanical and structural engineering applications.
Geometric Conditions and Assumptions
Axisymmetric stress conditions assume a rotational symmetry about a central axis, where the geometry, loading, and boundary conditions are invariant along the circumferential direction, simplifying the three-dimensional problem into a two-dimensional analysis in the radial and axial coordinates. Plane stress conditions apply to thin structures where the stress components perpendicular to the plane (typically the thickness direction) are negligible, assuming zero out-of-plane stresses, which reduces the problem to two dimensions within the plane of the structure. The geometric assumption for axisymmetric analysis is a solid of revolution, whereas plane stress applies to flat plates or thin shells where thickness is small compared to other dimensions.
Mathematical Formulation of Axisymmetric Analysis
Axisymmetric analysis simplifies the three-dimensional elasticity problem by using cylindrical coordinates where all variables depend only on radial and axial coordinates, assuming no variation in the circumferential direction. The mathematical formulation involves solving equilibrium equations, strain-displacement relations, and constitutive equations explicitly adapted for axisymmetric conditions, accounting for radial (r), axial (z), and hoop (th) stresses and strains. Unlike plane stress analysis, which assumes zero stress through the thickness, axisymmetric analysis captures the hoop stress component, making it essential for structures like pressure vessels and rotationally symmetric bodies.
Mathematical Formulation of Plane Stress Analysis
Plane stress analysis mathematically models thin structures by assuming zero stress perpendicular to the plane, reducing the 3D state of stress to a 2D problem defined by s_x, s_y, and t_xy components. The governing equations employ equilibrium equations, compatibility conditions, and Hooke's law under plane stress assumptions, where s_z = t_xz = t_yz = 0, simplifying the constitutive relations and strain-displacement relations. Finite element methods often implement this formulation using 2D elements, enabling efficient computation of stress and strain distributions in thin plates and shells under in-plane loading.
Key Differences between Axisymmetric and Plane Stress
Axisymmetric stress analysis assumes a rotational symmetry around a central axis, simplifying 3D problems into 2D by considering radial, axial, and hoop stresses, essential for cylindrical structures under uniform loading. Plane stress assumes that stresses perpendicular to the plane are negligible, typically applied in thin flat components where out-of-plane stresses are minimal. Axisymmetric conditions involve three non-zero stress components (radial, axial, hoop), while plane stress has only two significant stresses (in-plane), making axisymmetric analysis suitable for rotational bodies and plane stress for thin flat geometries.
Applicability in Engineering Problems
Axisymmetric analysis is preferred for structures with rotational symmetry, such as pressure vessels, pipes, and cylindrical tanks, enabling efficient computation of stresses and deformations under axisymmetric loading conditions. Plane stress models apply to thin flat components like plates and shells where stress through the thickness is negligible, making them suitable for analyzing thin-walled structures under in-plane loading. Understanding the geometry and loading conditions of the engineering problem guides the selection between axisymmetric and plane stress models to ensure accurate and computationally efficient simulations.
Advantages and Limitations of Each Approach
Axisymmetric analysis simplifies three-dimensional problems with rotational symmetry into two-dimensional models, significantly reducing computational effort while maintaining accuracy for structures like pressure vessels and pipes; however, it is limited to geometries and loading conditions that are symmetrical around an axis. Plane stress analysis assumes stresses normal to the plane are negligible, making it suitable for thin structures such as plates and sheets, but it cannot accurately capture stress distributions in thick or complex 3D components. Both methods optimize computational resources for specific structural problems, with axisymmetric analysis excelling in rotationally symmetric scenarios and plane stress offering efficiency for thin, flat geometries.
Real-World Examples and Case Studies
Axisymmetric analysis is crucial in designing components like pressure vessels, pipelines, and rotating disks where geometry and loading are symmetrical around an axis, ensuring accurate stress and deformation predictions. Plane stress assumptions apply effectively to thin plates and aerospace skin panels subjected to in-plane loads, simplifying stress analysis in areas such as aircraft wing design and automotive body panels. Real-world case studies demonstrate the use of axisymmetric modeling in nuclear reactor pressure tubes, while plane stress analysis optimizes structural integrity in bridge decks and electronic circuit boards.
Choosing the Right Analysis Method
Choosing the right analysis method between axisymmetric and plane stress depends on the geometry and loading conditions of the structure. Axisymmetric analysis is ideal for rotationally symmetric models subjected to symmetrical loading, enabling efficient computation by reducing the problem to two dimensions. In contrast, plane stress analysis suits thin, flat components where stresses perpendicular to the surface are negligible, ensuring accurate modeling of in-plane forces and deformations.
Axisymmetric Infographic
 libterm.com
libterm.com