Prandtl analogy explains the relationship between momentum transfer and heat transfer in turbulent flow, helping engineers predict heat transfer rates based on fluid velocity profiles. This concept bridges fluid dynamics and thermodynamics, enhancing the design of efficient cooling systems and heat exchangers. Explore the article to understand how Prandtl analogy can optimize your engineering solutions.
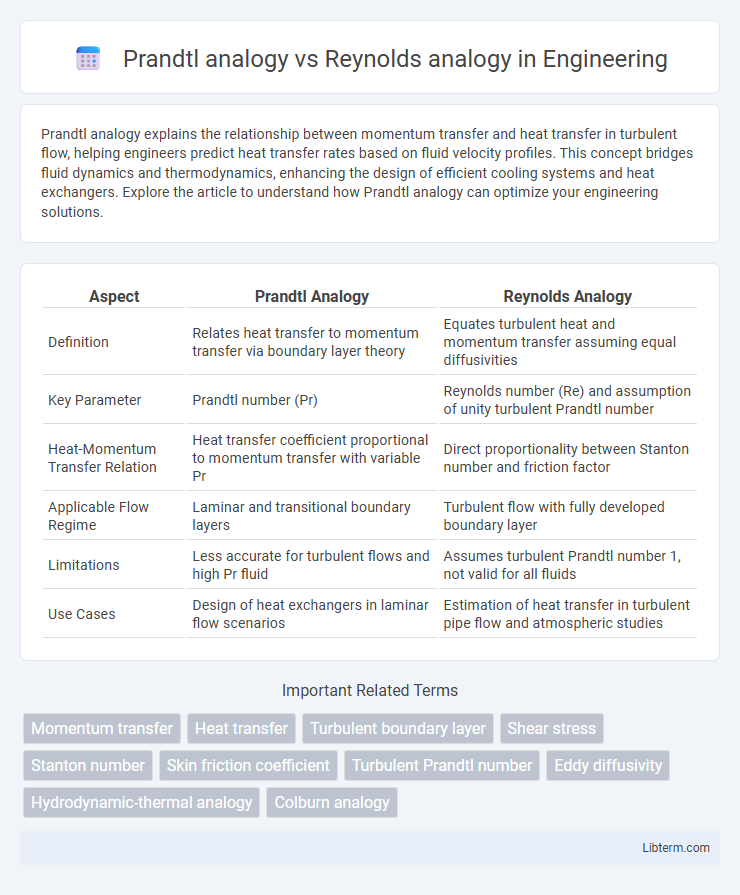
Table of Comparison
| Aspect | Prandtl Analogy | Reynolds Analogy |
|---|---|---|
| Definition | Relates heat transfer to momentum transfer via boundary layer theory | Equates turbulent heat and momentum transfer assuming equal diffusivities |
| Key Parameter | Prandtl number (Pr) | Reynolds number (Re) and assumption of unity turbulent Prandtl number |
| Heat-Momentum Transfer Relation | Heat transfer coefficient proportional to momentum transfer with variable Pr | Direct proportionality between Stanton number and friction factor |
| Applicable Flow Regime | Laminar and transitional boundary layers | Turbulent flow with fully developed boundary layer |
| Limitations | Less accurate for turbulent flows and high Pr fluid | Assumes turbulent Prandtl number 1, not valid for all fluids |
| Use Cases | Design of heat exchangers in laminar flow scenarios | Estimation of heat transfer in turbulent pipe flow and atmospheric studies |
Introduction to Heat and Momentum Transfer Analogies
Prandtl analogy and Reynolds analogy are fundamental concepts in heat and momentum transfer, establishing relationships between thermal and velocity boundary layers. Prandtl analogy refines the Reynolds analogy by accounting for the Prandtl number, linking the turbulent momentum and heat transfer more accurately in fluids with varying thermal diffusivity. These analogies are essential for simplifying complex convective heat transfer calculations in engineering applications involving fluid flow and heat exchange.
Overview of Prandtl Analogy
Prandtl analogy establishes a relationship between momentum and heat transfer in turbulent flow, linking the friction factor with the Nusselt number through the Stanton number. It assumes that the turbulent transport mechanisms for momentum and heat are similar, allowing experimental correlations of heat transfer to be derived from velocity profiles. This analogy is widely used in engineering to estimate heat transfer rates in pipes and boundary layers where turbulent flow dominates.
Overview of Reynolds Analogy
Reynolds analogy establishes a direct relationship between momentum and heat transfer in turbulent flow, assuming equal turbulent diffusivities for both quantities. This analogy simplifies the calculation of heat transfer coefficients by correlating them with measured friction factors, making it particularly useful for engineering applications involving convective heat transfer. Unlike the Prandtl analogy, Reynolds analogy often assumes a Prandtl number close to unity, limiting its accuracy in fluids with significantly different thermal and momentum diffusivities.
Mathematical Formulation: Prandtl vs Reynolds
The Prandtl analogy mathematically relates turbulent momentum and heat transfer through the equation St = f/2, where St is the Stanton number and f is the Darcy friction factor, incorporating the turbulence Prandtl number for more accurate heat transfer prediction. Reynolds analogy simplifies this by equating momentum and heat transfer coefficients directly, assuming the turbulent Prandtl number equals one, expressed as St = f/2 without adjustments. The Prandtl analogy provides better precision in cases where the momentum and thermal diffusivities differ, while Reynolds analogy offers a more straightforward approach under the assumption of equal diffusivities.
Physical Assumptions and Applicability
Prandtl analogy assumes a linear relationship between momentum and heat transfer in turbulent flow, relying on the concept of eddy diffusivity being equal for both quantities, which applies best to constant property fluids with moderate Prandtl numbers. Reynolds analogy, on the other hand, presumes identical turbulent transport mechanisms for heat and momentum without considering molecular diffusion, making it more applicable to flows with Prandtl numbers close to unity and simple shear flows. The physical assumptions of Prandtl analogy offer greater flexibility in varying Prandtl number regimes, while Reynolds analogy is primarily suited for idealized conditions where thermal and momentum boundary layers align closely.
Key Differences between Prandtl and Reynolds Analogies
Prandtl analogy relates the turbulent momentum transfer to heat transfer by incorporating the turbulent Prandtl number, highlighting the difference in diffusivities of momentum and heat, typically around 0.85 to 0.9. Reynolds analogy assumes equal diffusivities with a turbulent Prandtl number of one, directly linking Stanton number to skin friction coefficient, which simplifies calculations but can lead to inaccuracies in heat transfer predictions. Key differences include Prandtl analogy's accommodation of varying thermal and momentum diffusivities versus Reynolds analogy's assumption of their equivalence.
Limitations and Validity Range of Each Analogy
The Prandtl analogy applies primarily to turbulent flow over smooth surfaces with moderate pressure gradients but loses accuracy in laminar or highly separated flows due to its assumption of similar momentum and heat transfer mechanisms. The Reynolds analogy is valid mainly for fully turbulent flows with constant fluid properties and negligible viscous dissipation, but it fails in cases with variable viscosity, high heat flux, or significant buoyancy effects. Both analogies are limited by their oversimplified treatment of turbulence and heat transfer coupling, necessitating caution when extending their use beyond canonical flow conditions.
Experimental Validation and Comparisons
Experimental validation of Prandtl and Reynolds analogies frequently involves turbulent pipe and boundary layer flows, where measured heat transfer and momentum transfer data are compared. The Reynolds analogy assumes a direct proportionality between momentum and heat transfer coefficients, often validated in fluids with Prandtl number close to unity, while Prandtl's analogy introduces a correction factor accounting for variable Prandtl numbers, yielding better accuracy in experimental data involving gases and liquids. Comparative studies reveal Prandtl analogy's superiority in predicting heat transfer under various turbulent flow conditions, especially when empirical friction factor correlations align closely with measured values.
Practical Applications in Engineering
Prandtl analogy is extensively used in heat transfer engineering to relate momentum and heat transfer coefficients in turbulent flow, facilitating the design of efficient heat exchangers and cooling systems. Reynolds analogy simplifies the prediction of heat and mass transfer rates by assuming similar turbulent transport mechanisms, making it valuable in aerodynamic surface cooling and chemical reactor design. Engineers often choose Prandtl analogy for complex fluid dynamics involving varying Prandtl numbers, whereas Reynolds analogy is preferred for low-Prandtl-number fluids due to its simplified assumptions.
Summary and Future Perspectives
Prandtl analogy and Reynolds analogy both provide foundational frameworks for understanding the relationship between momentum and heat transfer in turbulent flows, with Prandtl analogy emphasizing the equivalence of turbulent diffusivities for momentum and heat, and Reynolds analogy simplifying the heat transfer coefficient as proportional to the friction factor. Recent advancements in turbulence modeling and computational fluid dynamics enable more precise quantification of discrepancies between these analogies under varying flow and thermal conditions, highlighting the need for hybrid or modified analogies to improve predictive accuracy. Future perspectives focus on integrating machine learning techniques and high-fidelity simulations to refine these analogies, enhancing their applicability in complex industrial applications such as aerodynamic design and heat exchanger optimization.
Prandtl analogy Infographic
 libterm.com
libterm.com