Mach number represents the ratio of an object's speed to the speed of sound in the surrounding medium, crucial in aerodynamics for classifying flight regimes from subsonic to hypersonic. Understanding the Mach number is essential for optimizing aircraft performance, reducing drag, and ensuring structural integrity at various speeds. Discover how Mach number influences your travel and engineering designs in the rest of this article.
Table of Comparison
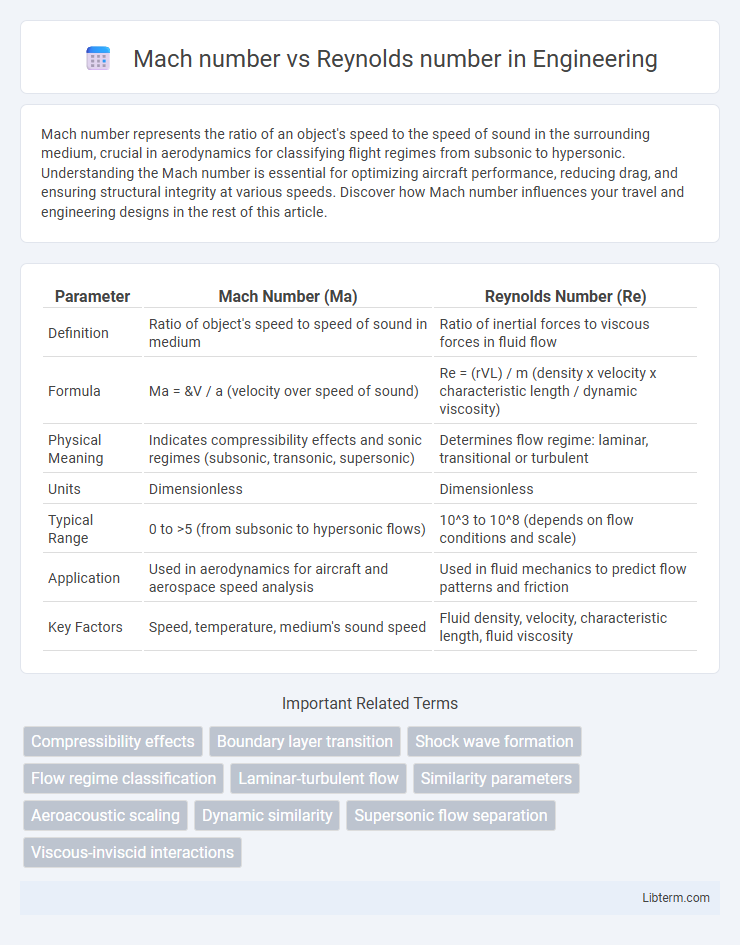
| Parameter | Mach Number (Ma) | Reynolds Number (Re) |
|---|---|---|
| Definition | Ratio of object's speed to speed of sound in medium | Ratio of inertial forces to viscous forces in fluid flow |
| Formula | Ma = &V / a (velocity over speed of sound) | Re = (rVL) / m (density x velocity x characteristic length / dynamic viscosity) |
| Physical Meaning | Indicates compressibility effects and sonic regimes (subsonic, transonic, supersonic) | Determines flow regime: laminar, transitional or turbulent |
| Units | Dimensionless | Dimensionless |
| Typical Range | 0 to >5 (from subsonic to hypersonic flows) | 10^3 to 10^8 (depends on flow conditions and scale) |
| Application | Used in aerodynamics for aircraft and aerospace speed analysis | Used in fluid mechanics to predict flow patterns and friction |
| Key Factors | Speed, temperature, medium's sound speed | Fluid density, velocity, characteristic length, fluid viscosity |
Introduction to Mach Number and Reynolds Number
Mach number quantifies the speed of an object moving through a fluid relative to the speed of sound in that medium, critical for analyzing compressible flow regimes in aerospace engineering. Reynolds number measures the ratio of inertial forces to viscous forces within a fluid, essential for predicting flow patterns such as laminar or turbulent behavior around objects. Both dimensions are fundamental in fluid dynamics to understand and model aerodynamic properties across various velocity and viscosity conditions.
Fundamental Definitions and Formulas
Mach number quantifies the ratio of an object's speed to the local speed of sound and is expressed as M = V / a, where V represents the flow velocity and a denotes the speed of sound in the medium. Reynolds number characterizes the ratio of inertial forces to viscous forces in fluid flow, defined by Re = rVD / m, where r is fluid density, V is velocity, D is characteristic length, and m is dynamic viscosity. Both dimensionless numbers are critical for analyzing aerodynamic and fluid dynamic behavior, influencing flow regimes, compressibility effects, and boundary layer development.
Physical Significance in Fluid Dynamics
Mach number quantifies the ratio of an object's speed to the local speed of sound, crucial for analyzing compressibility effects and shock wave formation in high-speed flows. Reynolds number characterizes the ratio of inertial forces to viscous forces, determining flow regimes such as laminar or turbulent behavior and influencing boundary layer development. Together, these dimensionless numbers govern fluid flow characteristics by linking velocity, viscosity, density, and compressibility in aerospace and engineering applications.
How Mach Number Influences Flow Behavior
Mach number significantly influences flow behavior by determining compressibility effects in fluid dynamics. At low Mach numbers (below 0.3), flow can be treated as incompressible, whereas higher Mach numbers lead to compressible flow with shock waves and changes in density. This transition directly affects aerodynamic characteristics, including pressure distribution, drag, and boundary layer behavior.
The Role of Reynolds Number in Flow Regimes
Reynolds number critically defines flow regimes by quantifying the ratio of inertial forces to viscous forces within a fluid, influencing whether the flow is laminar, transitional, or turbulent. Lower Reynolds numbers indicate laminar flow characterized by smooth, orderly fluid motion, while higher values correspond to turbulence with chaotic eddies and vortices. Understanding Reynolds number behavior is essential for accurate prediction of flow characteristics in aerodynamics, pipe flow, and heat transfer applications, especially when analyzed alongside Mach number, which captures compressibility effects.
Key Differences Between Mach Number and Reynolds Number
Mach number quantifies the ratio of an object's speed to the speed of sound in the surrounding medium, indicating compressibility effects in fluid flow. Reynolds number measures the ratio of inertial forces to viscous forces, determining the flow regime as laminar or turbulent. Key differences include Mach number's focus on compressibility and speed relative to sound, while Reynolds number assesses flow stability based on fluid velocity, characteristic length, and viscosity.
Applications in Aerodynamics and Engineering
Mach number and Reynolds number are critical parameters in aerodynamics and engineering, governing flow characteristics around objects. The Mach number indicates compressibility effects and shock wave formation in high-speed flight, essential for designing supersonic aircraft and missiles. Reynolds number influences boundary layer behavior and turbulence, impacting aerodynamic performance, heat transfer, and structural loading in applications ranging from wind turbines to automotive aerodynamics.
Mach Number and Reynolds Number in Compressible Flows
Mach Number signifies the ratio of flow velocity to the local speed of sound, crucial in analyzing compressible flows where density variations affect fluid behavior. Reynolds Number, defined as the ratio of inertial forces to viscous forces, influences the transition between laminar and turbulent flow regimes but its effect is modified in compressible flows due to changes in fluid properties with pressure and temperature. Understanding the interplay between Mach Number and Reynolds Number enables accurate prediction of shock waves, boundary layer behavior, and aerodynamic performance in high-speed fluid dynamics.
Practical Examples and Case Studies
Mach number and Reynolds number play crucial roles in aerospace engineering, especially when analyzing airflow over aircraft wings. In practical case studies, supersonic jets like the Concorde exhibit high Mach numbers around 2.0, significantly affecting shock wave formation and drag, while maintaining Reynolds numbers that determine boundary layer behavior and transition. Wind tunnel experiments on commercial airliners routinely adjust Reynolds numbers to replicate real-flight conditions, aiding in the optimization of wing design for fuel efficiency and stability.
Summary and Implications for Future Research
Mach number quantifies the ratio of an object's speed to the speed of sound, influencing compressibility effects in fluid flow, while Reynolds number represents the ratio of inertial forces to viscous forces, determining flow regime characteristics such as laminar or turbulent behavior. Understanding the interplay between Mach and Reynolds numbers is critical for designing aerospace vehicles, optimizing performance under varying atmospheric conditions, and improving computational fluid dynamics models. Future research should focus on high-fidelity simulations and experimental validation at extreme values to better predict transition phenomena and aerodynamic heating in hypersonic flight.
Mach number Infographic
 libterm.com
libterm.com