State-space analysis offers a powerful method to model and understand complex dynamic systems by representing them through a set of first-order differential or difference equations. This approach captures the system's internal state, inputs, and outputs, making it essential for control design, stability assessment, and system behavior prediction. Explore the rest of the article to unlock deeper insights into how state-space analysis can enhance your control system applications.
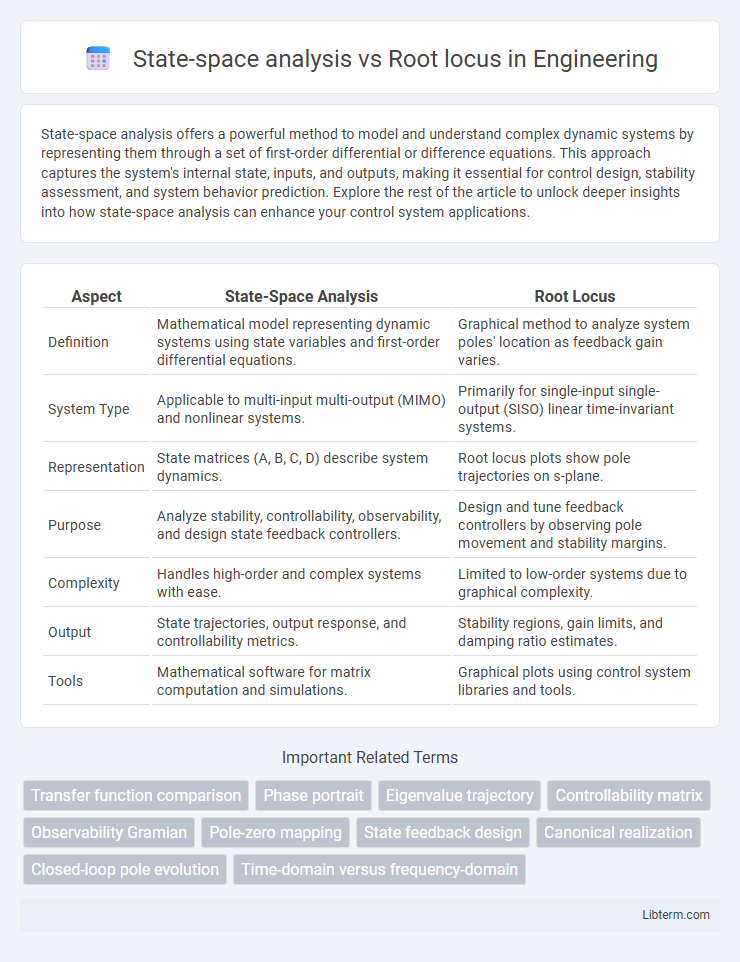
Table of Comparison
| Aspect | State-Space Analysis | Root Locus |
|---|---|---|
| Definition | Mathematical model representing dynamic systems using state variables and first-order differential equations. | Graphical method to analyze system poles' location as feedback gain varies. |
| System Type | Applicable to multi-input multi-output (MIMO) and nonlinear systems. | Primarily for single-input single-output (SISO) linear time-invariant systems. |
| Representation | State matrices (A, B, C, D) describe system dynamics. | Root locus plots show pole trajectories on s-plane. |
| Purpose | Analyze stability, controllability, observability, and design state feedback controllers. | Design and tune feedback controllers by observing pole movement and stability margins. |
| Complexity | Handles high-order and complex systems with ease. | Limited to low-order systems due to graphical complexity. |
| Output | State trajectories, output response, and controllability metrics. | Stability regions, gain limits, and damping ratio estimates. |
| Tools | Mathematical software for matrix computation and simulations. | Graphical plots using control system libraries and tools. |
Introduction to State-Space Analysis and Root Locus
State-space analysis represents dynamic systems using a set of first-order differential equations with vectors and matrices, enabling comprehensive modeling of multi-input multi-output systems and time-domain behavior. Root locus graphically depicts the paths of system poles in the s-plane as a system parameter, typically gain, varies, providing intuitive insights into system stability and transient response. While state-space methods offer a holistic framework for modern control design and observer implementation, root locus remains valuable for classical control system stability and compensator design.
Fundamental Concepts: Definitions and Key Principles
State-space analysis represents dynamic systems through a set of first-order differential equations using state variables, capturing the complete system behavior in vector-matrix form. Root locus plots graphically illustrate how the roots of a system's characteristic equation change with varying parameters, emphasizing system stability and transient response. Both methods provide critical insights into control system design, with state-space focusing on time-domain dynamics and root locus on frequency-domain pole placement.
Mathematical Representation in State-Space vs Root Locus
State-space analysis represents dynamic systems using a set of first-order differential equations encapsulated in matrix form, typically expressed as \(\dot{x} = Ax + Bu\) and \(y = Cx + Du\), where \(A\), \(B\), \(C\), and \(D\) are system matrices defining the system dynamics and output. Root locus analysis, on the other hand, uses polynomial equations derived from the characteristic equation of the system, plotting the locus of closed-loop pole locations in the complex plane as a system parameter, usually gain, varies. While state-space provides a comprehensive, multidimensional framework for time-domain analysis allowing modern control techniques like LQR and observer design, root locus focuses on stability and transient response through graphical interpretation of pole movements in the s-plane.
System Stability: State-Space Methods vs Root Locus Techniques
State-space analysis evaluates system stability by examining eigenvalues of the system matrix, providing a comprehensive view of multi-input multi-output (MIMO) systems and time-domain dynamics. Root locus techniques focus on the trajectory of closed-loop poles in the s-plane as system gain varies, offering intuitive insights for single-input single-output (SISO) systems. While root locus is effective for gain-based stability assessment, state-space methods enable stability analysis through Lyapunov criteria and controllability/observability checks, crucial for complex control design.
Controllability and Observability: A State-Space Perspective
State-space analysis provides a robust framework for assessing controllability and observability by examining system matrices (A, B, C, D), enabling precise matrix rank tests through the controllability and observability matrices. Root locus, primarily a frequency-domain method, offers limited insight into these properties as it focuses on pole movement and system stability rather than system state structure. Controllability in state-space ensures all states can be driven by inputs, while observability guarantees state estimation from outputs, both critical for advanced control design absent in traditional root locus evaluations.
Time-Domain vs Frequency-Domain Approaches
State-space analysis provides a robust time-domain approach by modeling system dynamics through differential equations, capturing multi-input multi-output behaviors and internal state variables. Root locus focuses on the frequency-domain perspective, graphing how pole locations shift with varying gain to assess system stability and transient response. While state-space excels in modern control design and simulation of complex systems, root locus remains valuable for intuitive visualization of closed-loop system poles and controller tuning.
Design Applications: Where State-Space Excels vs Root Locus
State-space analysis excels in designing multi-input multi-output (MIMO) control systems, offering a complete representation of system dynamics through matrices that handle complex state variables efficiently. Root locus is ideal for single-input single-output (SISO) systems, providing intuitive graphical insights into pole movement and stability during controller gain adjustments. State-space methods enable modern control design techniques such as optimal control and observer design, which are less accessible through root locus approaches.
Visualization and Interpretation of System Behavior
State-space analysis offers a multidimensional visualization of system behavior by representing system dynamics through matrices that capture all state variables simultaneously, enabling detailed time-domain interpretation. Root locus provides a graphical method focused on the movement of closed-loop poles in the complex plane as system parameters vary, offering insights into system stability and transient response. Visualization through state-space can reveal interactions between states, while root locus emphasizes how pole locations affect overall system performance.
Strengths and Limitations: Comparative Analysis
State-space analysis excels in handling multi-input multi-output (MIMO) systems and provides a comprehensive time-domain representation, enabling analysis of controllability, observability, and state feedback design. Root locus techniques offer intuitive graphical insight into the stability and transient response of single-input single-output (SISO) control systems by illustrating pole movement with varying gain. Limitations include state-space complexity for high-order nonlinear systems and less visual clarity in MIMO cases, while root locus is restricted primarily to linear, SISO systems and does not directly address state feedback or time-domain performance metrics.
Selecting the Appropriate Method for Control Systems
State-space analysis offers a comprehensive framework for multi-input, multi-output (MIMO) systems and time-varying dynamics, making it ideal for modern complex control applications requiring state feedback and observers. Root locus excels in single-input, single-output (SISO) systems by visually illustrating how pole locations vary with gain changes, facilitating controller design based on system stability and transient response. Selecting between these methods depends on system complexity, with state-space favored for high-dimensional or nonlinear models and root locus preferred for intuitive gain tuning in simpler linear systems.
State-space analysis Infographic
 libterm.com
libterm.com