An influence matrix helps identify and analyze the relationships and impact between various factors or stakeholders within a system. Understanding this tool allows you to prioritize actions and allocate resources effectively for better decision-making. Explore the rest of the article to learn how to create and apply an influence matrix for your projects.
Table of Comparison
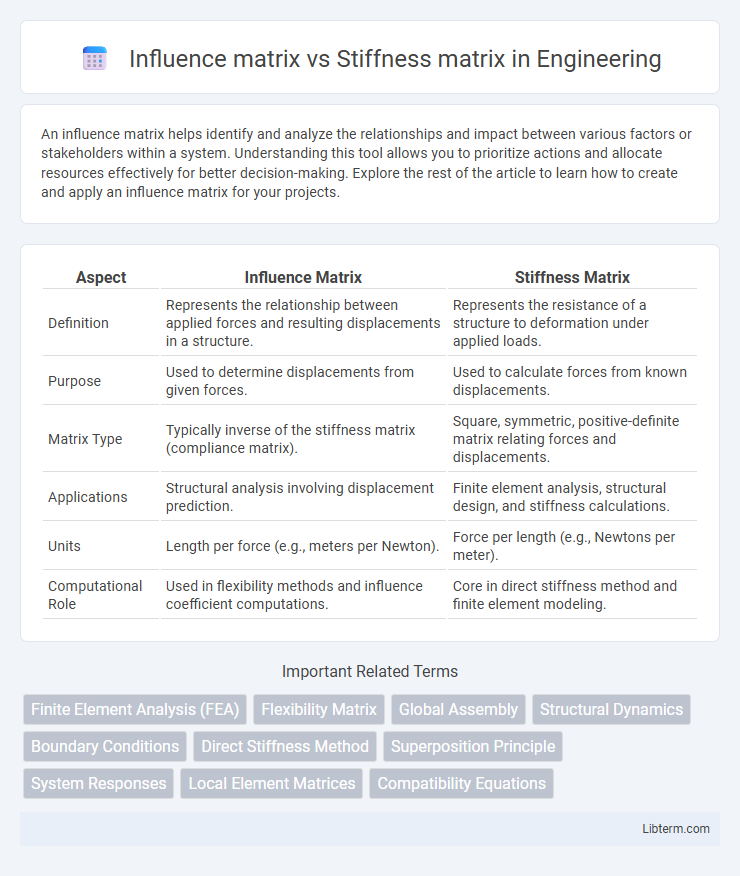
| Aspect | Influence Matrix | Stiffness Matrix |
|---|---|---|
| Definition | Represents the relationship between applied forces and resulting displacements in a structure. | Represents the resistance of a structure to deformation under applied loads. |
| Purpose | Used to determine displacements from given forces. | Used to calculate forces from known displacements. |
| Matrix Type | Typically inverse of the stiffness matrix (compliance matrix). | Square, symmetric, positive-definite matrix relating forces and displacements. |
| Applications | Structural analysis involving displacement prediction. | Finite element analysis, structural design, and stiffness calculations. |
| Units | Length per force (e.g., meters per Newton). | Force per length (e.g., Newtons per meter). |
| Computational Role | Used in flexibility methods and influence coefficient computations. | Core in direct stiffness method and finite element modeling. |
Introduction to Influence Matrix and Stiffness Matrix
The Influence Matrix represents the relationship between applied forces and resulting displacements in structural analysis, capturing how each unit load affects all degrees of freedom. The Stiffness Matrix, central to finite element methods, defines the resistance of a structure to deformation by linking displacements directly to internal forces through material and geometric properties. Both matrices are fundamental in solving boundary value problems and form the basis for understanding structural behavior under various loading conditions.
Fundamental Concepts of Structural Analysis
The influence matrix represents the relationship between applied forces and resulting displacements at specific points in a structure, capturing the flexibility characteristics, whereas the stiffness matrix relates nodal displacements directly to applied forces, reflecting the rigidity of the structure. In structural analysis, the stiffness matrix is symmetric and positive definite, facilitating the solution of equilibrium equations via methods like the finite element method (FEM). Understanding the distinction between influence and stiffness matrices is essential for analyzing indeterminate structures, where influence matrices help assess displacement influence coefficients while stiffness matrices enable force-displacement computations.
Definition and Mathematical Representation
The influence matrix quantifies the response of a system's degrees of freedom to unit loads, representing how a force at one point influences displacements at other points, typically formulated as a matrix of displacement responses under unit loads. The stiffness matrix represents the linear relationship between nodal displacements and applied forces in structural systems, mathematically defined by \( \mathbf{K} \mathbf{u} = \mathbf{f} \), where \( \mathbf{K} \) is the stiffness matrix, \( \mathbf{u} \) the displacement vector, and \( \mathbf{f} \) the force vector. While the stiffness matrix focuses on force-displacement causality, the influence matrix emphasizes displacement responses to unit forces, often used in boundary element methods and structural analysis.
Role of Influence Matrix in Structural Engineering
The influence matrix plays a crucial role in structural engineering by representing the displacement response at particular points due to unit loads applied at other points, facilitating the analysis of indeterminate structures. Unlike the stiffness matrix, which relates forces to displacements through structural rigidity, the influence matrix directly captures deflection patterns and load interactions without explicitly considering material properties. This matrix is essential for influence line construction, sensitivity analysis, and in methods like the force method, enhancing the understanding of how loads affect structural behavior under varying conditions.
Functionality of Stiffness Matrix in Finite Element Method
The stiffness matrix in the Finite Element Method (FEM) represents the relationship between nodal displacements and applied forces, embodying the structural rigidity and resistance to deformation of the element. Unlike the influence matrix, which maps applied loads to displacements directly, the stiffness matrix is fundamental in assembling the global system of equations to solve for unknown displacements. Its functionality ensures accurate modeling of mechanical behavior and efficient numerical solution of structural analysis problems.
Comparative Analysis: Influence Matrix vs Stiffness Matrix
The Influence Matrix and Stiffness Matrix serve distinct functions in structural analysis, with the latter directly relating forces to corresponding displacements through stiffness coefficients, making it fundamental for solving linear elasticity problems. The Influence Matrix, also known as the flexibility matrix, reflects displacement responses due to unit loads and is particularly useful in systems where displacement measurements drive the analysis. Compared to the Stiffness Matrix, the Influence Matrix provides greater insight into system flexibility, but is generally less straightforward to invert for solving problems, highlighting a trade-off between interpretability and computational efficiency in comparative applications.
Applications in Civil and Mechanical Engineering
The influence matrix and stiffness matrix are crucial tools in structural analysis within civil and mechanical engineering; the stiffness matrix specifically quantifies the rigidity of structures by relating nodal displacements to applied forces, widely used in finite element methods for designing buildings, bridges, and mechanical components. The influence matrix, conversely, maps the response at one point of a structure to loads applied at other points, proving essential in boundary element methods for analyzing stress and displacement in complex geometries and foundation problems. Engineers leverage the stiffness matrix for modeling elastic behavior in frames and shells, while the influence matrix aids in understanding system sensitivities and load redistribution in soil-structure interaction and vibration analysis.
Advantages and Limitations of Each Matrix
The Influence matrix, often used in boundary element methods, efficiently handles infinite or semi-infinite domain problems by reducing dimensionality and focusing on boundary variables, but it can become computationally expensive for complex geometries due to dense matrix formation. The Stiffness matrix, fundamental in finite element analysis, provides sparse, symmetric matrices that are computationally efficient and compatible with iterative solvers, yet it requires discretization of the entire domain and may struggle with unbounded problems. Influence matrices excel in boundary-only formulations with clearer physical interpretation, whereas stiffness matrices are advantageous for problems demanding domain discretization and localized property variations.
Practical Examples and Case Studies
Influence matrices are commonly used in boundary element methods for solving potential flow and elasticity problems, such as modeling groundwater flow through porous media or stress analysis in soil mechanics. Stiffness matrices are fundamental in finite element analysis for structural engineering tasks like bridge design or aircraft wing stress predictions, providing a direct relationship between nodal displacements and forces. Case studies in civil engineering demonstrate that influence matrix approaches excel in large-scale geotechnical problems with complex boundaries, while stiffness matrices offer efficient solutions for detailed stress-strain analysis in localized structural components.
Conclusion: Choosing the Right Matrix for Structural Analysis
The stiffness matrix is ideal for direct finite element analysis due to its straightforward representation of structural rigidity and compatibility with standard displacement-based methods. The influence matrix excels in boundary element methods, efficiently capturing boundary effects without meshing the entire domain, making it preferable for problems with infinite or semi-infinite domains. Selecting the right matrix depends on the problem domain, computational resources, and desired accuracy, with stiffness matrices suited for volumetric discretization and influence matrices optimized for boundary-only discretization.
Influence matrix Infographic
 libterm.com
libterm.com