Structural indeterminacy occurs when a structure has insufficient constraints to determine internal forces and reactions uniquely, leading to potential displacement or instability. Understanding this concept is crucial for designing safe buildings and bridges, as it influences load distribution and overall structural behavior. Explore the rest of the article to learn how engineers manage and analyze structural indeterminacy.
Table of Comparison
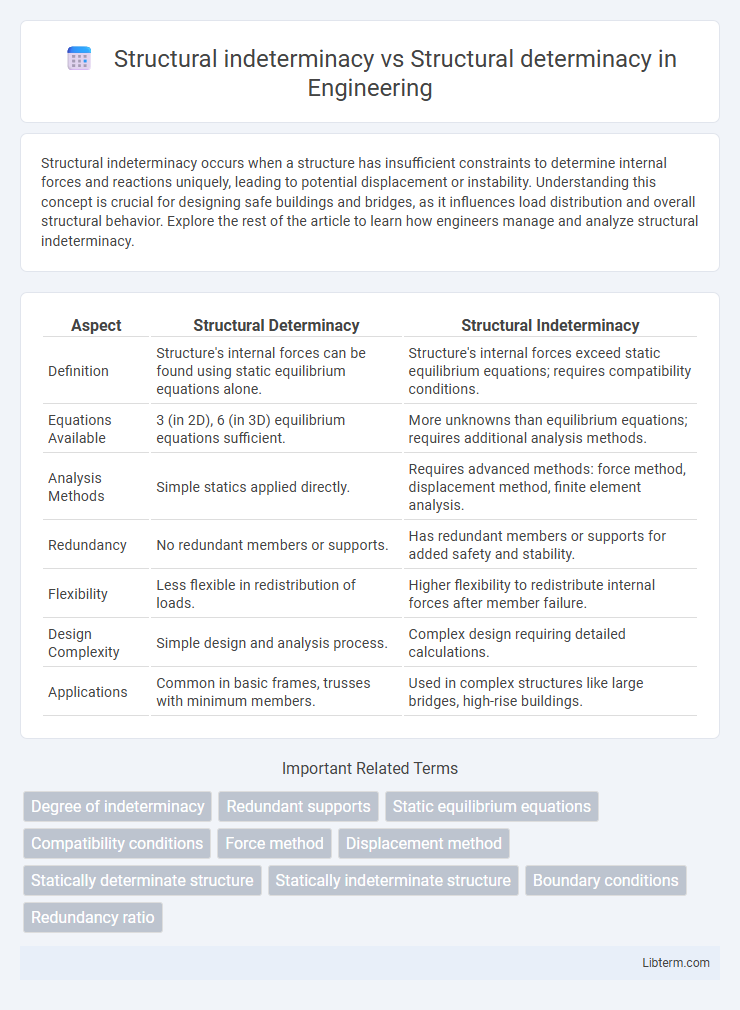
| Aspect | Structural Determinacy | Structural Indeterminacy |
|---|---|---|
| Definition | Structure's internal forces can be found using static equilibrium equations alone. | Structure's internal forces exceed static equilibrium equations; requires compatibility conditions. |
| Equations Available | 3 (in 2D), 6 (in 3D) equilibrium equations sufficient. | More unknowns than equilibrium equations; requires additional analysis methods. |
| Analysis Methods | Simple statics applied directly. | Requires advanced methods: force method, displacement method, finite element analysis. |
| Redundancy | No redundant members or supports. | Has redundant members or supports for added safety and stability. |
| Flexibility | Less flexible in redistribution of loads. | Higher flexibility to redistribute internal forces after member failure. |
| Design Complexity | Simple design and analysis process. | Complex design requiring detailed calculations. |
| Applications | Common in basic frames, trusses with minimum members. | Used in complex structures like large bridges, high-rise buildings. |
Introduction to Structural Analysis
Structural determinacy occurs when the internal forces and reactions in a structure can be determined solely from the equilibrium equations, making the system statically determinate. Structural indeterminacy arises when there are more unknown forces than equilibrium equations, requiring compatibility conditions and material properties for analysis. Understanding the distinction between determinate and indeterminate structures is fundamental in structural analysis for accurate load prediction and safety assessment.
Defining Structural Determinacy
Structural determinacy occurs when a structure's internal forces and reactions can be uniquely determined using only the equations of equilibrium, reflecting a balance between unknowns and available equations. This concept ensures the structure is stable and can resist applied loads without deformation changes that can't be predicted. In contrast, structural indeterminacy arises when there are more unknown forces than equilibrium equations, requiring compatibility conditions or material properties to analyze the system fully.
Understanding Structural Indeterminacy
Structural indeterminacy occurs when the equilibrium equations are insufficient to determine all internal forces and support reactions, often requiring methods like compatibility equations or finite element analysis for resolution. It contrasts with structural determinacy, where internal forces and reactions can be found solely from static equilibrium conditions. Understanding structural indeterminacy is crucial for analyzing complex frameworks such as continuous beams and rigid frames, where multiple load paths and redundancies exist.
Key Differences Between Determinate and Indeterminate Structures
Structural determinacy occurs when a structure's internal forces can be calculated solely from equilibrium equations, ensuring unique solutions for reactions and member forces. In contrast, structural indeterminacy arises when additional compatibility equations are necessary due to redundant supports or members, making analysis more complex. Determinate structures are typically simpler and more economical to analyze, whereas indeterminate structures offer greater stability and load distribution capabilities.
Criteria for Determinacy in Structural Systems
Structural determinacy is assessed by comparing the number of unknown support reactions and internal member forces to the available equilibrium equations, typically three in two-dimensional structures and six in three-dimensional structures. Structural systems are determinate when the number of unknowns equals the number of equilibrium equations, allowing all forces and moments to be solved solely through static equilibrium. If the unknowns exceed the equilibrium constraints, the structure is indeterminate, requiring compatibility conditions and deformation analysis to determine internal forces and reactions.
Advantages of Determinate Structures
Determinate structures offer clear advantages, including simplified analysis because their internal forces and reactions can be calculated using only the equations of equilibrium. This straightforward predictability reduces computational effort and enhances reliability in design, minimizing the risk of unexpected failures. Their stability under varied loading conditions makes determinate structures particularly suitable for rapid construction and cost-effective engineering solutions.
Benefits of Indeterminate Structures
Indeterminate structures offer enhanced load distribution, allowing multiple pathways for stress transfer and improving overall safety during unexpected loads or damage. Their ability to redistribute forces reduces the likelihood of structural failure, resulting in increased durability and resilience. These advantages lead to more economical use of materials and greater design flexibility compared to determinate structures.
Methods for Analyzing Indeterminate Structures
Methods for analyzing indeterminate structures include the force method, displacement method, and finite element analysis, which address additional unknown forces beyond equilibrium equations. The force method involves releasing redundant supports and applying compatibility conditions to solve for unknown forces, while the displacement method uses displacement compatibility to determine internal forces and deformations. Finite element analysis offers a numerical approach that discretizes the structure into elements to handle complex indeterminacies with greater accuracy and flexibility.
Practical Applications in Engineering Design
Structural indeterminacy enables engineers to design complex frameworks that redistribute loads efficiently through multiple pathways, enhancing safety and flexibility in bridges, buildings, and aerospace structures. In contrast, structural determinacy simplifies analysis and construction by relying on clearly defined support conditions and member forces, often preferred in straightforward designs such as small residential buildings and basic trusses. Balancing structural indeterminacy with determinacy ensures optimized material use, cost-effectiveness, and resilience against dynamic loads in practical engineering design.
Conclusion: Choosing the Right Structural Approach
Choosing the right structural approach hinges on understanding the balance between structural indeterminacy and determinacy to ensure safety, efficiency, and cost-effectiveness. Structural determinacy offers straightforward analysis and predictable load paths, ideal for simple designs, while indeterminate structures provide enhanced stiffness and load distribution suitable for complex, high-performance systems. Engineers must evaluate factors such as material behavior, load conditions, and construction feasibility to optimize design choices, leveraging advanced computational tools for precise modeling of indeterminate structures.
Structural indeterminacy Infographic
 libterm.com
libterm.com