Matrix multiplication is a fundamental operation in linear algebra, combining two matrices to produce a third matrix that represents the composite transformation or relationship between data sets. Understanding how to multiply matrices correctly is essential for applications in computer graphics, physics simulations, and machine learning. Explore the rest of this article to master the step-by-step process and practical uses of matrix multiplication for your projects.
Table of Comparison
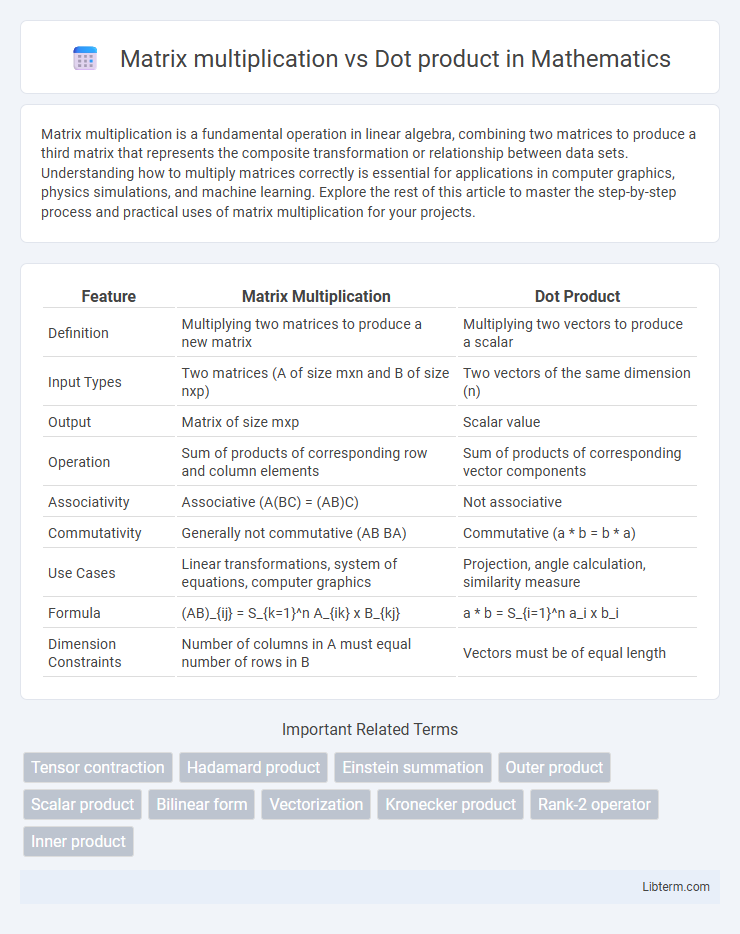
| Feature | Matrix Multiplication | Dot Product |
|---|---|---|
| Definition | Multiplying two matrices to produce a new matrix | Multiplying two vectors to produce a scalar |
| Input Types | Two matrices (A of size mxn and B of size nxp) | Two vectors of the same dimension (n) |
| Output | Matrix of size mxp | Scalar value |
| Operation | Sum of products of corresponding row and column elements | Sum of products of corresponding vector components |
| Associativity | Associative (A(BC) = (AB)C) | Not associative |
| Commutativity | Generally not commutative (AB BA) | Commutative (a * b = b * a) |
| Use Cases | Linear transformations, system of equations, computer graphics | Projection, angle calculation, similarity measure |
| Formula | (AB)_{ij} = S_{k=1}^n A_{ik} x B_{kj} | a * b = S_{i=1}^n a_i x b_i |
| Dimension Constraints | Number of columns in A must equal number of rows in B | Vectors must be of equal length |
Introduction to Matrix Multiplication and Dot Product
Matrix multiplication involves combining two matrices by multiplying rows of the first matrix with columns of the second to produce a new matrix, essential in linear transformations and systems of equations. The dot product, a specific type of matrix operation, calculates the sum of products of corresponding entries in two equal-length vectors, resulting in a scalar. Understanding these operations is fundamental in fields like computer graphics, machine learning, and physics.
Defining Matrix Multiplication
Matrix multiplication involves combining two matrices by multiplying the rows of the first matrix by the columns of the second matrix, resulting in a new matrix with dimensions defined by the outer dimensions of the multiplied matrices. Each element in the resulting matrix is computed as the sum of the products of corresponding elements from the row of the first matrix and the column of the second matrix. Unlike the dot product, which produces a scalar from two vectors, matrix multiplication produces a matrix that represents linear transformations or compositions of transformations.
Understanding the Dot Product
The dot product is a specific operation between two vectors resulting in a scalar, calculated by multiplying corresponding components and summing the products. Matrix multiplication involves combining rows and columns of two matrices to produce a new matrix, where the dot product computes each element. Understanding the dot product is fundamental as it measures vector similarity and projections, serving as the building block within matrix multiplication processes.
Key Differences Between Matrix Multiplication and Dot Product
Matrix multiplication involves combining two matrices by multiplying rows of the first matrix with columns of the second, resulting in a new matrix, while the dot product is a specific operation that multiplies two equal-length vectors element-wise and sums the results, producing a scalar. Matrix multiplication requires that the number of columns in the first matrix equals the number of rows in the second, whereas the dot product solely operates on vectors of equal dimensions. The key difference lies in output types: matrix multiplication yields a matrix, expanding dimensionality, whereas the dot product yields a scalar, summarizing the similarity or projection between vectors.
Mathematical Representation and Notation
Matrix multiplication is represented as C = AB, where A is an mxn matrix and B is an nxp matrix, producing an mxp matrix C, with each element c_ij calculated as the sum of products of corresponding elements from the i-th row of A and the j-th column of B (c_ij = S_k=1^n a_ik * b_kj). The dot product, denoted as a * b or
Common Applications in Mathematics and Engineering
Matrix multiplication is essential in linear algebra for transforming coordinate systems, solving systems of linear equations, and performing state-space analysis in control engineering. The dot product is widely used to calculate projections, measure vector similarity in signal processing, and compute work done in physics through force and displacement vectors. Both operations underpin algorithms in machine learning, computer graphics, and digital signal processing, facilitating efficient data manipulation and geometric transformations.
Computational Complexity and Performance
Matrix multiplication involves the product of two matrices with computational complexity typically O(n^3) for naive algorithms, while optimized algorithms like Strassen's reduce this to approximately O(n^2.81). The dot product is a simpler operation between two vectors with a linear complexity of O(n), making it computationally less expensive and significantly faster in performance for comparable input sizes. Performance differences become prominent in large-scale applications, where matrix multiplication demands more memory bandwidth and processing power compared to the dot product's straightforward scalar output.
Visualization and Geometric Interpretation
Matrix multiplication represents the transformation of one matrix by another, visualized as applying linear transformations to vectors or entire coordinate systems, often resulting in rotations, scalings, or shears in multidimensional space. The dot product, interpreted geometrically, measures the projection of one vector onto another, quantifying their directional similarity through the cosine of the angle between them. Visualizing the dot product as the length of the shadow of one vector onto another provides clear insight into vector orthogonality and magnitude relations, while matrix multiplication extends these concepts to complex, combined transformations.
Practical Examples and Use Cases
Matrix multiplication is widely used in computer graphics to transform 3D coordinates, enabling realistic rendering of images by combining rotation, scaling, and translation matrices. The dot product is essential in machine learning algorithms, particularly for calculating cosine similarity between feature vectors to measure their orientation in high-dimensional space. In physics, dot products quantify work done by a force acting at an angle, while matrix multiplication facilitates solving systems of linear equations in engineering simulations.
Conclusion: Choosing Between Matrix Multiplication and Dot Product
Matrix multiplication and dot product serve distinct roles in linear algebra with matrix multiplication handling operations between matrices to produce another matrix, while the dot product calculates a scalar from two vectors, reflecting their directional similarity. Selection depends on the mathematical context: use matrix multiplication for transformations, systems of equations, and combining linear mappings, while the dot product is ideal for measuring vector projections, angles, and magnitudes. In computational applications, matrix multiplication often demands higher computational resources compared to the simpler, faster dot product, influencing the choice based on efficiency requirements and problem complexity.
Matrix multiplication Infographic
 libterm.com
libterm.com