Understanding well-orders, partial orders, total orders, preorders, and linear orders helps clarify the hierarchy and relationships within sets, where each type defines specific rules for comparing elements. You can identify a well-order as a total order where every non-empty subset has a least element, while partial orders allow incomparable elements, unlike total or linear orders that require comparability. Explore the rest of this article to deepen your grasp of these fundamental order relations and their applications.
Table of Comparison
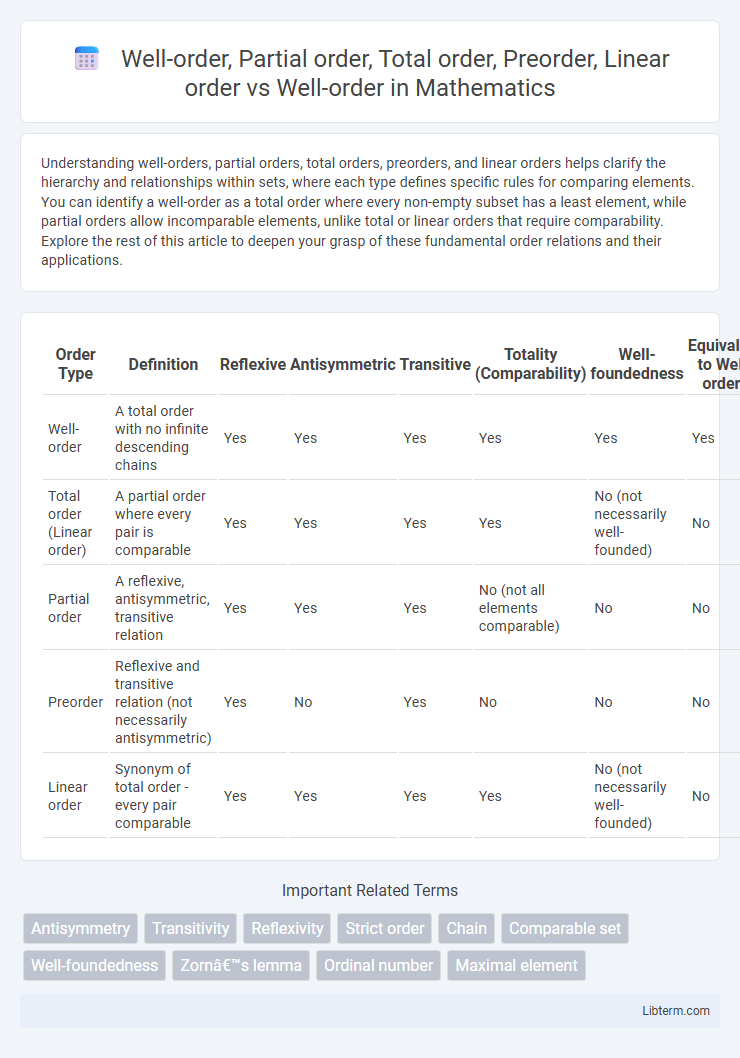
| Order Type | Definition | Reflexive | Antisymmetric | Transitive | Totality (Comparability) | Well-foundedness | Equivalent to Well-order? |
|---|---|---|---|---|---|---|---|
| Well-order | A total order with no infinite descending chains | Yes | Yes | Yes | Yes | Yes | Yes |
| Total order (Linear order) | A partial order where every pair is comparable | Yes | Yes | Yes | Yes | No (not necessarily well-founded) | No |
| Partial order | A reflexive, antisymmetric, transitive relation | Yes | Yes | Yes | No (not all elements comparable) | No | No |
| Preorder | Reflexive and transitive relation (not necessarily antisymmetric) | Yes | No | Yes | No | No | No |
| Linear order | Synonym of total order - every pair comparable | Yes | Yes | Yes | Yes | No (not necessarily well-founded) | No |
Introduction to Ordering Relations in Mathematics
Ordering relations in mathematics define structured ways to compare elements within a set, starting with preorders that ensure reflexivity and transitivity but may lack antisymmetry, evolving into partial orders which add antisymmetry to prevent cycles. Total orders extend partial orders by requiring comparability between any two elements, while well-orders refine total orders by guaranteeing every non-empty subset has a least element, crucial for induction and recursion principles. Linear order is often synonymous with total order, emphasizing a strict sequence without gaps, whereas well-orders impose additional structure facilitating foundational arguments in set theory and ordinal analysis.
Understanding Preorders: The Foundation of Ordered Sets
Preorders form the foundational concept in the study of ordered sets by defining a binary relation that is reflexive and transitive but not necessarily antisymmetric. Unlike partial orders, preorders may identify distinct elements as equivalent, which are then treated as a single entity in the induced partial order by quotienting the equivalence relation. Understanding preorders is essential for grasping more structured relations like partial orders, total orders, linear orders, and well-orders, where additional properties such as antisymmetry and comparability refine the hierarchy and impose stricter organizational rules.
Defining Partial Orders: Properties and Examples
Partial orders are binary relations that are reflexive, antisymmetric, and transitive, allowing elements to be compared in a structured yet non-linear manner, exemplified by set inclusion () among subsets. Well-orders are a specific type of total order where every non-empty subset has a least element, ensuring no infinite descending sequences, as seen in the natural numbers (N) with standard ordering. Preorders relax antisymmetry, being reflexive and transitive but potentially allowing equivalences, whereas linear orders require comparability between all elements, making every total order a linear order but a linear order only a total order if it also satisfies well-order conditions.
Exploring Total Orders: Structure and Significance
Total orders, also known as linear orders, arrange elements so every pair is comparable, forming a structure critical in sorting algorithms and decision theory. Exploring total orders reveals their significance in ensuring consistency and predictability within sets, where every element can be precisely positioned relative to others. Unlike well-orders, total orders do not require every non-empty subset to have a least element, highlighting the nuanced relationship between these order types in mathematical and computer science applications.
Well-Orders: Concept, Characteristics, and Applications
Well-orders are a special class of total orders characterized by every non-empty subset having a least element, ensuring no infinite descending chains exist and enabling transfinite induction. They are fundamental in set theory for defining ordinal numbers and analyzing order types, with applications extending to proof theory, computer science, and combinatorics. Unlike linear orders, well-orders impose a stricter structure facilitating well-founded recursion and guaranteeing termination in algorithms.
Key Differences Between Partial and Total Orders
Partial order is a binary relation that is reflexive, antisymmetric, and transitive, allowing some elements to be incomparable, whereas total order is a partial order with the additional property that every pair of elements is comparable. In a total order, all elements are arranged in a linear sequence, while partial orders permit subsets where elements may not have a defined order. The key difference lies in comparability: total orders require complete comparability of elements, whereas partial orders do not.
Linear Order vs Well-Order: A Comparative Analysis
Linear order is a reflexive, antisymmetric, transitive relation that arranges elements in a sequence where every pair is comparable, while well-order extends linear order by requiring every non-empty subset to have a least element. Unlike linear orders, well-orders guarantee the existence of minimal elements for subsets, essential in transfinite induction and ordinal analysis. This distinction underpins foundational concepts in set theory, where well-orders enable ordinal classification beyond mere comparability.
Well-Orderings and the Principle of Transfinite Induction
Well-orderings are total orders with the added property that every non-empty subset has a least element, enabling the use of the Principle of Transfinite Induction for proofs extending beyond finite sets. Partial orders relax comparability between elements, while preorders lack antisymmetry, and linear orders coincide with total orders where every pair is comparable. Understanding the distinction between well-orderings and linear orders centers on well-foundedness, which is crucial for defining ordinal numbers and conducting transfinite induction in set theory and logic.
Applications of Ordered Sets in Mathematics and Computer Science
Well-orders are essential in transfinite induction and ordinal theory, providing a foundation for proofs involving infinite sequences and sets. Partial orders model hierarchical data structures and task scheduling in computer science, enabling dependency management and optimization. Total orders and linear orders facilitate sorting algorithms and database indexing, while well-orders guarantee termination of recursive algorithms and support formal verification in theoretical computer science.
Summary: Importance of Ordered Structures in Mathematical Theory
Ordered structures such as well-orders, partial orders, total orders, preorders, and linear orders form the foundation for comparing and organizing elements within sets, enabling rigorous abstraction in mathematics. Well-orders are crucial in set theory and transfinite induction due to their guarantee that every non-empty subset has a least element, while partial orders model hierarchies with incomparable elements, and total or linear orders impose complete comparability. Understanding these distinct ordered relations facilitates advancements in logic, algebra, and computer science by structuring data, defining processes, and proving properties in a coherent, hierarchical framework.
Well-order, Partial order, Total order, Preorder, Linear order Infographic
 libterm.com
libterm.com