Radius is a fundamental geometric concept representing the distance from the center of a circle or sphere to any point on its boundary, crucial for calculating area and volume. Understanding the radius allows you to solve various mathematical and real-world problems involving circles, spheres, and arcs. Explore the rest of the article to discover detailed formulas, applications, and tips for mastering radius-related calculations.
Table of Comparison
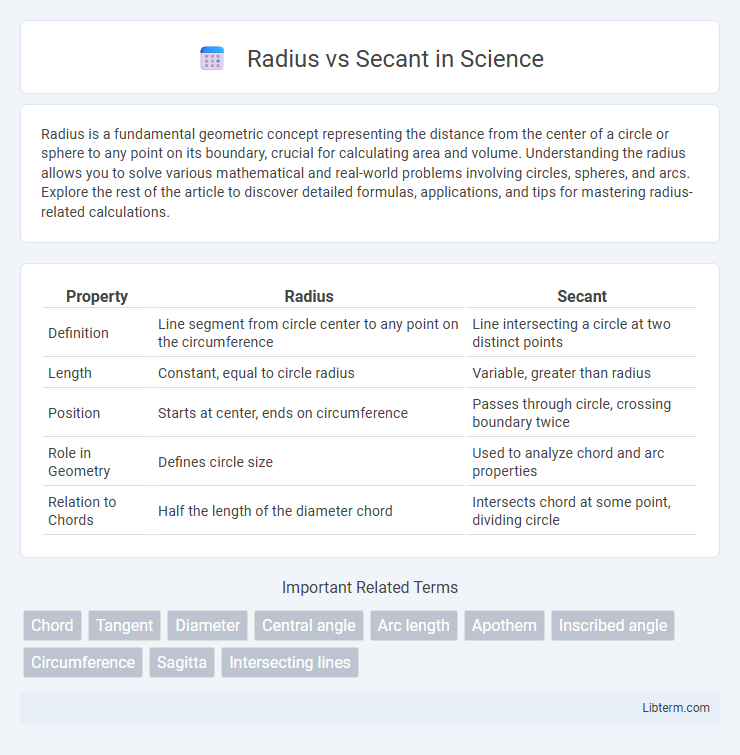
| Property | Radius | Secant |
|---|---|---|
| Definition | Line segment from circle center to any point on the circumference | Line intersecting a circle at two distinct points |
| Length | Constant, equal to circle radius | Variable, greater than radius |
| Position | Starts at center, ends on circumference | Passes through circle, crossing boundary twice |
| Role in Geometry | Defines circle size | Used to analyze chord and arc properties |
| Relation to Chords | Half the length of the diameter chord | Intersects chord at some point, dividing circle |
Introduction to Radius and Secant
A radius is a line segment connecting the center of a circle to any point on its circumference, representing the constant distance from the center to the edge. A secant is a line that intersects a circle at two distinct points, extending beyond the circle's circumference. Understanding the properties of both the radius and secant is fundamental in circle geometry and helps solve problems involving arcs, chords, and angles.
Defining the Radius in Geometry
The radius in geometry is defined as the line segment connecting the center of a circle to any point on its circumference, representing a constant distance throughout the circle. Unlike the secant, which intersects the circle at two points and extends beyond the circumference, the radius is confined within the circle's boundary. The radius is fundamental in calculating properties such as the circle's diameter, area, and circumference.
Understanding the Secant Line
The secant line intersects a circle at two distinct points, providing a chord that reveals important properties of the circle's geometry. Unlike the radius, which extends from the center to a single point on the circumference, the secant line captures the relationship between those two intersection points, often used to approximate tangents or calculate angles. Understanding the secant line is essential in trigonometry and calculus for studying curves and their behavior around a circle.
Key Differences Between Radius and Secant
The key difference between radius and secant lies in their definitions and geometric roles: a radius is a line segment connecting the center of a circle to any point on its circumference, while a secant is a line that intersects the circle at exactly two points, extending beyond the circle's boundary. The radius always measures the fixed distance from the center to the edge, essential for calculating circle properties such as area and circumference. In contrast, the secant's length varies and is used in chord-related calculations and the study of circle intersections.
Mathematical Formulas Involving Radius and Secant
The radius of a circle is defined as the line segment from its center to any point on the circumference, with length r, while a secant is a line intersecting the circle at two points. The fundamental relationship involving a radius and a secant is expressed through the secant-tangent theorem: if a secant segment intersects a tangent from a common external point, the length of the tangent squared equals the product of the lengths of the entire secant segment and its external part, (PT)^2 = PA x PB. In trigonometric terms, the secant function sec(th) is the reciprocal of the cosine function, relating angle th to radius r and secant length s through s = r x sec(th).
Visual Representation: Radius vs Secant
A radius is a line segment connecting the center of a circle to any point on its circumference, visually depicted as a straight line inside the circle extending from the center to the edge. A secant, in contrast, is a line that intersects the circle at two distinct points, often drawn extending beyond the circle on both sides, cutting through the circumference. The radius highlights the fixed distance from the center, while the secant emphasizes a chord-like intersection crossing the circle entirely.
Real-world Applications of Radius and Secant
The radius of a circle is crucial in engineering and architecture for designing curves, arches, and circular components, ensuring structural integrity and precise measurements. Secants find applications in navigation and surveying by intersecting circular paths or boundaries, aiding in accurate distance calculations and mapping. Both concepts are fundamental in physics for analyzing circular motion and wave patterns, enhancing practical problem-solving in technology and science.
Common Misconceptions Explained
Radius and secant lines are often confused, but the radius is a line segment from the center of a circle to any point on its circumference, while a secant is a line that intersects the circle at exactly two points. Common misconceptions include thinking a radius can extend beyond the circle or that a secant only touches one point. Understanding these distinctions clarifies circle geometry and supports accurate calculations involving arcs, chords, and angles.
Radius and Secant in Trigonometry
In trigonometry, a radius is a line segment from the center of a circle to any point on its circumference, crucial for defining angles and constructing trigonometric functions. A secant, in contrast, is a line that intersects a circle at two points, often used to study chord properties and angles formed outside or inside the circle. Understanding the radius and secant relationship helps solve problems involving circle geometry, angle measures, and distances in trigonometric contexts.
Conclusion: Choosing Between Radius and Secant
Selecting between radius and secant depends on the geometric context and measurement needs; the radius consistently measures the shortest distance from the circle's center to its perimeter, while the secant intersects the circle at two points, providing chord-related insights. Radius is optimal for defining circle size and properties like circumference and area. Secant lines are preferable when analyzing intersecting chords, angles formed outside the circle, or segment lengths within the circle.
Radius Infographic
 libterm.com
libterm.com