Analytical approximation methods provide efficient solutions to complex mathematical problems by simplifying equations while maintaining accuracy. These techniques are crucial in fields such as physics, engineering, and economics where exact solutions are often unattainable. Explore the rest of this article to discover how you can apply these methods to optimize problem-solving in your work.
Table of Comparison
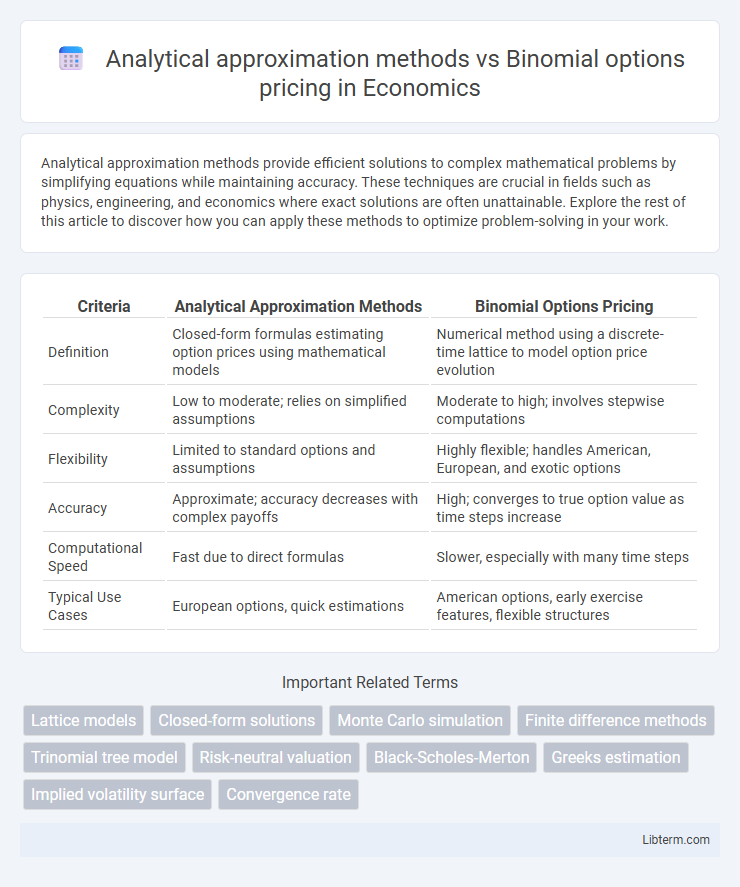
| Criteria | Analytical Approximation Methods | Binomial Options Pricing |
|---|---|---|
| Definition | Closed-form formulas estimating option prices using mathematical models | Numerical method using a discrete-time lattice to model option price evolution |
| Complexity | Low to moderate; relies on simplified assumptions | Moderate to high; involves stepwise computations |
| Flexibility | Limited to standard options and assumptions | Highly flexible; handles American, European, and exotic options |
| Accuracy | Approximate; accuracy decreases with complex payoffs | High; converges to true option value as time steps increase |
| Computational Speed | Fast due to direct formulas | Slower, especially with many time steps |
| Typical Use Cases | European options, quick estimations | American options, early exercise features, flexible structures |
Introduction to Option Pricing Models
Option pricing models are essential for valuing derivatives, with the Binomial Options Pricing Model providing a discrete-time framework that models possible price movements through a recombining tree structure. Analytical approximation methods, such as the Black-Scholes formula, offer closed-form solutions by assuming continuous-time price dynamics, enabling faster computations for European-style options. Comparing these approaches highlights trade-offs between computational efficiency, model complexity, and the ability to handle American-style options or path-dependency.
Overview of Analytical Approximation Methods
Analytical approximation methods provide efficient ways to estimate option prices when exact solutions like the Binomial options pricing model become computationally expensive or infeasible. Techniques such as the Black-Scholes formula and perturbation methods leverage continuous-time assumptions and closed-form expressions for quicker valuation of European-style options. These approximations often balance accuracy and speed, making them suitable for real-time trading and risk management compared to the discrete-step binomial approach.
Fundamentals of the Binomial Options Pricing Model
The Binomial Options Pricing Model (BOPM) fundamentally relies on constructing a discrete-time lattice to model possible future asset prices, enabling the calculation of option value by backward induction through these price nodes. Analytical approximation methods often simplify or assume continuous price movements and volatility, whereas BOPM provides a flexible framework to handle American options and features like early exercise by evaluating option payoff at each node. The model's core principle involves computing the expected option payoff under a risk-neutral measure, discounting it at the risk-free rate to present value, thereby capturing the probabilistic nature of price changes across multiple periods.
Comparative Accuracy: Analytical vs. Binomial Approaches
Analytical approximation methods, such as the Black-Scholes model, provide closed-form solutions offering high computational efficiency but may lack precision for American options or scenarios with complex features like dividends and early exercise. Binomial options pricing, involving iterative lattice-based computations, captures option value dynamics more accurately, especially for American-style options, by modeling path-dependent features and discrete exercise opportunities. The comparative accuracy favors binomial models in handling real-world complexities, though analytical methods remain preferable for their speed and simplicity in European-style option valuation.
Computational Complexity and Efficiency
Analytical approximation methods, such as the Black-Scholes model, typically offer lower computational complexity with closed-form solutions enabling rapid option pricing under certain assumptions. In contrast, the Binomial options pricing model involves iterative tree-based computations with complexity increasing linearly with the number of time steps, trading off computational efficiency for greater flexibility in handling American options and path dependency. Computational efficiency in option pricing is highly affected by model choice, where analytical solutions excel in speed, while binomial models provide accuracy and adaptability at the cost of increased processing time.
Flexibility in Handling Exotic Options
Analytical approximation methods offer greater flexibility in handling exotic options by accommodating complex payoff structures and path dependencies that standard models often struggle to address. The Binomial options pricing model, while intuitive and versatile for American options, becomes computationally intensive and less practical for highly path-dependent or multi-asset exotic derivatives. Advanced approximation techniques can efficiently capture nuanced features of exotic options, enabling more accurate pricing and risk assessment in diverse market conditions.
Sensitivity to Volatility and Interest Rate Changes
Analytical approximation methods often provide faster estimates of option prices but can be less accurate in capturing sensitivity to volatility and interest rate changes compared to the Binomial options pricing model. The Binomial model explicitly models the path-dependent nature of these sensitivities by simulating multiple underlying price movements over time, allowing for more precise Greeks calculation. Volatility shifts cause nonlinear impacts that the Binomial model adapts to more robustly, while interest rate changes affect discounting and risk-neutral probabilities more directly within its lattice framework.
Practical Use Cases and Industry Preferences
Analytical approximation methods such as the Black-Scholes model offer fast and straightforward option price estimates suitable for European options under constant volatility assumptions, making them highly favored in equity markets. The Binomial options pricing model provides greater flexibility by accommodating American options and varying volatility or dividend schedules, which is preferred in markets requiring early exercise features like employee stock options or commodities trading. Industry practitioners often select analytical approaches for high-frequency trading and risk management due to computational efficiency, while the binomial model is favored in valuation scenarios requiring accuracy in discrete time steps and complex payoff structures.
Limitations and Assumptions of Each Method
Analytical approximation methods, such as the Black-Scholes model, assume constant volatility and continuous trading, which limits their accuracy in capturing market realities like jumps or stochastic volatility. Binomial options pricing models rely on discrete time steps and assume recombining price trees, leading to computational intensity for finer accuracy but better adaptability to American options and early exercise features. Both methods require assumptions about market behavior that can cause valuation errors, with analytical methods struggling under non-lognormal price distributions and binomial models facing exponential growth in complexity with increased steps.
Future Trends in Option Pricing Methodologies
Analytical approximation methods, such as closed-form solutions and series expansions, provide faster and often more computationally efficient alternatives to the Binomial options pricing model, especially for complex derivatives and high-dimensional problems. Future trends in option pricing methodologies emphasize hybrid models that integrate machine learning techniques with traditional analytical frameworks to improve accuracy and adaptability to market dynamics. The evolution towards real-time data assimilation and enhanced volatility modeling aims to overcome limitations inherent in binomial approaches, fostering more precise and scalable option valuation.
Analytical approximation methods Infographic
 libterm.com
libterm.com