The Merton Jump Diffusion Model enhances traditional option pricing by incorporating sudden, significant jumps in asset prices alongside continuous Brownian motion, providing a more realistic representation of market behavior. This model captures the discontinuities in asset returns, allowing for better risk assessment and pricing accuracy in financial markets. Explore the rest of the article to understand how this model can improve your asset price predictions and option valuation strategies.
Table of Comparison
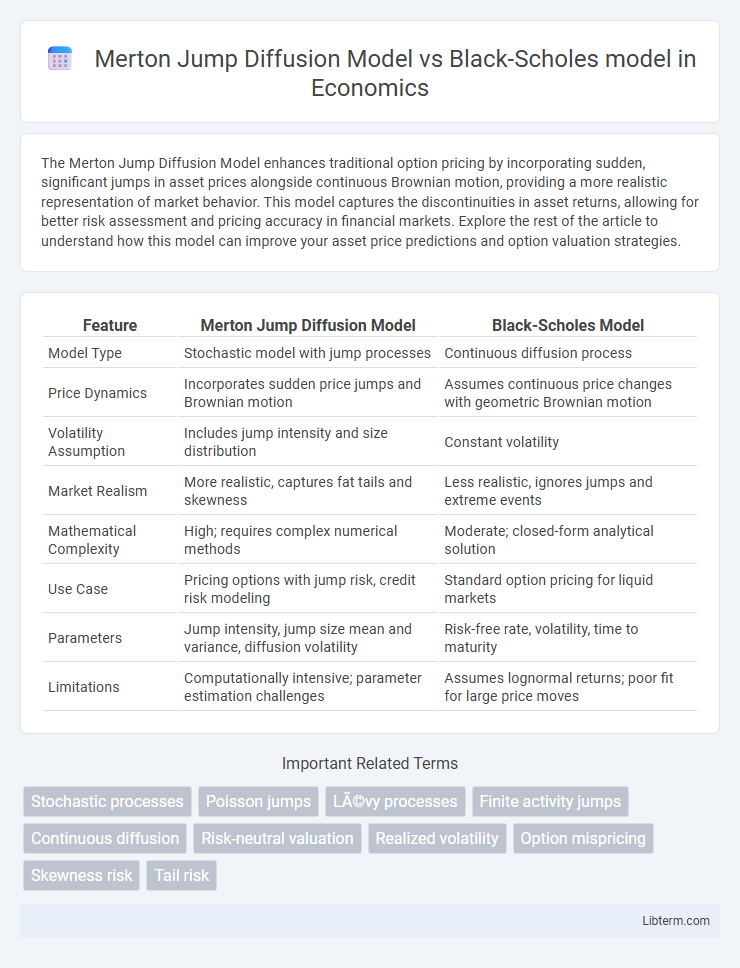
| Feature | Merton Jump Diffusion Model | Black-Scholes Model |
|---|---|---|
| Model Type | Stochastic model with jump processes | Continuous diffusion process |
| Price Dynamics | Incorporates sudden price jumps and Brownian motion | Assumes continuous price changes with geometric Brownian motion |
| Volatility Assumption | Includes jump intensity and size distribution | Constant volatility |
| Market Realism | More realistic, captures fat tails and skewness | Less realistic, ignores jumps and extreme events |
| Mathematical Complexity | High; requires complex numerical methods | Moderate; closed-form analytical solution |
| Use Case | Pricing options with jump risk, credit risk modeling | Standard option pricing for liquid markets |
| Parameters | Jump intensity, jump size mean and variance, diffusion volatility | Risk-free rate, volatility, time to maturity |
| Limitations | Computationally intensive; parameter estimation challenges | Assumes lognormal returns; poor fit for large price moves |
Introduction to Option Pricing Models
The Merton Jump Diffusion Model extends the Black-Scholes model by incorporating sudden jumps in asset prices, better capturing market realities such as crashes or spikes. While the Black-Scholes model assumes continuous price changes following a geometric Brownian motion, Merton's model introduces Poisson-distributed jumps for more accurate option pricing. This enhancement allows the Merton Jump Diffusion Model to address the limitations of Black-Scholes in modeling heavy-tailed distributions and volatility clustering observed in financial markets.
Overview of the Black-Scholes Model
The Black-Scholes model is a mathematical framework used to price European options by assuming a constant volatility and lognormal distribution of asset prices. It relies on the risk-neutral valuation principle and partial differential equations to derive a closed-form solution for option prices. Unlike the Merton Jump Diffusion model, Black-Scholes does not account for sudden jumps or discontinuities in asset prices, making it less accurate in capturing real market behaviors with abrupt price changes.
Fundamentals of the Merton Jump Diffusion Model
The Merton Jump Diffusion Model incorporates sudden, discrete jumps in asset prices alongside the continuous price changes modeled by the Black-Scholes framework, capturing more accurately the observed market phenomena such as price gaps and heavy tails in return distributions. It combines a Poisson jump process with a standard Brownian motion, allowing for both normal market fluctuations and unexpected, significant price movements, reflecting real market risks. This fundamental enhancement over the Black-Scholes model provides a better fit for option pricing in markets where jumps and volatility clustering occur.
Key Assumptions of Both Models
The Merton Jump Diffusion Model incorporates sudden, discontinuous jumps in asset prices, assuming the asset returns follow a combination of continuous Brownian motion and a Poisson jump process, capturing real market phenomena like crashes. The Black-Scholes model assumes continuous price movements with log-normal distribution and constant volatility, ignoring jumps and heavy tails in asset returns. Merton's model relaxes the Black-Scholes assumption of continuous trading and normality by including jump intensity and jump size distribution, providing a more realistic framework for pricing options under market uncertainties.
Mathematical Formulation: Black-Scholes vs Merton Jump Diffusion
The Black-Scholes model characterizes asset price dynamics through a continuous geometric Brownian motion defined by a stochastic differential equation with constant drift and volatility parameters. In contrast, the Merton Jump Diffusion model extends this framework by incorporating a Poisson-driven jump process, allowing for sudden discontinuous shifts in asset prices, mathematically represented by combining the standard Brownian motion with a compound Poisson process. This jump term introduces additional parameters such as jump intensity and jump size distribution, enhancing the model's capability to capture real market phenomena like leptokurtic returns and skewness, which are not addressed by the original Black-Scholes formulation.
Capturing Market Realities: Incorporating Jumps
The Merton Jump Diffusion Model enhances the Black-Scholes framework by integrating sudden price jumps, allowing for a more accurate representation of market realities such as abrupt stock price changes and extreme events. This model incorporates a Poisson jump process alongside the continuous diffusion process, capturing discontinuities missed by the Black-Scholes model's assumption of lognormality and continuous paths. By accounting for jumps, the Merton model better reflects market volatility and tail risk, improving option pricing and risk management under real-world conditions.
Comparative Strengths and Limitations
The Merton Jump Diffusion Model enhances the Black-Scholes model by incorporating sudden price jumps, capturing market discontinuities and better reflecting real asset price behaviors in volatile markets. While the Black-Scholes model assumes continuous price changes and constant volatility, making it simpler but less accurate during significant market shifts, the Merton model introduces complexity with jump intensity and size parameters that require calibration but improve option pricing accuracy for assets prone to abrupt movements. However, the Merton model's increased computational demand and parameter estimation challenges contrast with Black-Scholes' analytical tractability and widespread adoption in standard financial applications.
Practical Applications in Financial Markets
The Merton Jump Diffusion Model enhances option pricing accuracy by incorporating sudden, discontinuous asset price movements alongside continuous Brownian motion, making it highly effective for pricing options in markets with frequent jumps or shocks, such as equities during earnings announcements or market crises. In contrast, the Black-Scholes model assumes continuous price evolution with constant volatility, providing a simpler framework ideal for highly liquid, stable markets but often underestimating prices of options during volatile periods. Financial institutions leverage the Merton Jump Diffusion Model for risk management and hedging strategies in environments prone to abrupt price changes, while the Black-Scholes model remains foundational for standard derivative pricing and less volatile asset classes.
Model Calibration and Implementation Challenges
The Merton Jump Diffusion Model incorporates jumps in asset prices, requiring calibration of jump intensity, mean jump size, and jump volatility, which complicates parameter estimation compared to the Black-Scholes model's simpler volatility calibration. Calibration of the Merton model relies heavily on observed option prices across multiple maturities to accurately capture jump risk, often necessitating advanced numerical optimization techniques. Implementation challenges for the Merton model include increased computational complexity due to the jump component, while the Black-Scholes model, assuming continuous diffusion, benefits from closed-form solutions and faster calibration processes.
Conclusion: Choosing the Right Model for Option Pricing
The Merton Jump Diffusion Model incorporates sudden jumps in asset prices, capturing market realities like price discontinuities and heavy tails, making it superior for pricing options in volatile markets. The Black-Scholes model assumes continuous price changes and constant volatility, providing simplicity and analytical tractability but often underestimates risk in markets with abrupt movements. Selecting the right model depends on the underlying asset's behavior and market conditions; practitioners prioritize jump diffusion models for assets susceptible to sudden shocks, while Black-Scholes remains appropriate for stable, liquid markets.
Merton Jump Diffusion Model Infographic
 libterm.com
libterm.com