Hyperbolic discounting refers to the tendency for people to prefer smaller, immediate rewards over larger, delayed ones, often leading to impulsive decisions that undermine long-term goals. This cognitive bias affects financial planning, health choices, and everyday decision-making by distorting the perceived value of future benefits. Discover how understanding hyperbolic discounting can help you make smarter decisions by reading the rest of the article.
Table of Comparison
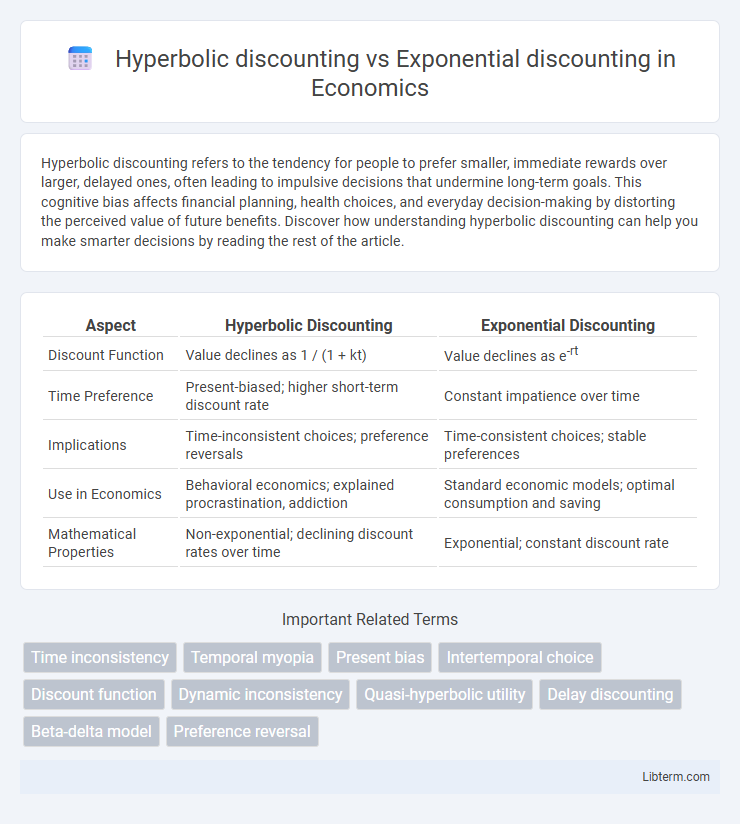
| Aspect | Hyperbolic Discounting | Exponential Discounting |
|---|---|---|
| Discount Function | Value declines as 1 / (1 + kt) | Value declines as e-rt |
| Time Preference | Present-biased; higher short-term discount rate | Constant impatience over time |
| Implications | Time-inconsistent choices; preference reversals | Time-consistent choices; stable preferences |
| Use in Economics | Behavioral economics; explained procrastination, addiction | Standard economic models; optimal consumption and saving |
| Mathematical Properties | Non-exponential; declining discount rates over time | Exponential; constant discount rate |
Introduction to Time Preference Theories
Time preference theories explain how individuals value rewards at different points in time, influencing decision-making and behavior. Hyperbolic discounting models a declining discount rate over time, reflecting a stronger preference for immediate rewards and a decreasing sensitivity to delays. Exponential discounting assumes a constant discount rate, leading to time-consistent choices and a steady devaluation of future rewards.
Understanding Hyperbolic Discounting
Hyperbolic discounting describes the tendency for people to prefer smaller, immediate rewards over larger, delayed rewards, reflecting a decline in perceived value that decreases more sharply for shorter delays. Unlike exponential discounting, which assumes a constant rate of time preference and consistent decision-making over time, hyperbolic discounting accounts for dynamic inconsistency and impulsivity in human behavior. Understanding hyperbolic discounting is crucial for explaining behaviors such as procrastination, addiction, and inconsistent financial decision-making in economics and psychology.
Exploring Exponential Discounting
Exponential discounting models future rewards by applying a constant discount rate over time, ensuring consistent time preferences that align with rational decision-making in economics and finance. This approach uses the formula \( V = \frac{A}{(1+r)^t} \), where \( V \) is the present value, \( A \) is the future amount, \( r \) is the discount rate, and \( t \) is time, supporting time-consistent evaluations of delayed rewards. In contrast to hyperbolic discounting, which captures decreasing impatience and preference reversals, exponential discounting assumes steady devaluation, making it foundational in traditional models like the discounted utility theory.
Mathematical Differences Between Hyperbolic and Exponential Models
Hyperbolic discounting uses a discount function of the form \( D(t) = \frac{1}{1 + kt} \), where \( k \) is the discount rate reflecting decreasing impatience over time, contrasting with exponential discounting's function \( D(t) = e^{-rt} \), where \( r \) is a constant discount rate implying consistent time preference. The hyperbolic model produces a declining discount rate \( \frac{k}{1+kt} \), capturing preference reversals and stronger short-term discounting, while exponential discounting maintains a constant instantaneous discount rate \( r \). Mathematically, hyperbolic discounting exhibits a non-constant hazard rate leading to dynamic inconsistency, whereas exponential discounting is time-consistent due to its memoryless property.
Behavioral Implications of Discounting Models
Hyperbolic discounting leads to time-inconsistent preferences, causing individuals to disproportionately favor immediate rewards over future gains, which often results in procrastination and impulsive decisions. Exponential discounting assumes consistent time preferences, leading to rational and stable intertemporal choices that support commitment to long-term goals. Understanding these behavioral implications helps in designing policies and interventions that counteract self-control problems and improve decision-making around savings, health, and consumption.
Real-Life Examples of Hyperbolic and Exponential Discounting
In real-life scenarios, hyperbolic discounting explains why people often prefer smaller, immediate rewards over larger, delayed ones, such as choosing to spend money now instead of saving for retirement. Exponential discounting, widely used in economic models, assumes consistent time preferences, exemplified by investors evaluating future cash flows with a steady discount rate. Behavioral studies show hyperbolic discounting better captures impulsive decisions like procrastination or addiction, while exponential discounting aligns with rational, long-term financial planning.
Impact on Decision Making and Self-Control
Hyperbolic discounting leads individuals to disproportionately prefer smaller, immediate rewards over larger, delayed rewards, resulting in inconsistent and impulsive decision-making that undermines long-term goals and self-control. In contrast, exponential discounting assumes a constant rate of decline in value over time, promoting more rational and stable choices aligned with future benefits. This difference in temporal valuation significantly influences behaviors related to saving, addiction, and habit formation by altering the perceived cost-benefit analysis across time.
Hyperbolic vs Exponential Discounting in Economics
Hyperbolic discounting models how individuals disproportionately prefer smaller, immediate rewards over larger, delayed rewards, reflecting decreasing impatience over time, contrasting with exponential discounting's constant rate of time preference. In economics, hyperbolic discounting better explains time-inconsistent behaviors and procrastination, as it captures the declining discount rate, whereas exponential discounting assumes a fixed discount factor leading to time-consistent choices. Empirical studies show hyperbolic discounting provides a more accurate representation of actual human decision-making in intertemporal choice situations such as savings and consumption.
Applications in Policy Design and Behavioral Interventions
Hyperbolic discounting better explains why individuals disproportionately prefer immediate rewards over future benefits, leading to time-inconsistent preferences that challenge traditional policy designs based on exponential discounting. In behavioral interventions, hyperbolic discounting informs commitment devices and incentive structures that help individuals stick to long-term goals by counteracting present bias. Policymakers leverage insights from hyperbolic discounting to create more effective programs addressing issues such as retirement savings, health behaviors, and addiction by aligning short-term incentives with long-term welfare.
Conclusion: Choosing the Right Discounting Model
Hyperbolic discounting better captures human tendencies for preference reversals and impulsive decision-making by valuing immediate rewards disproportionately higher than future ones. Exponential discounting provides consistent time-consistent preferences, making it ideal for modeling rational economic behavior and long-term financial planning. Selecting the appropriate discounting model depends on the context, with hyperbolic models suited for behavioral analysis and exponential models preferred for normative economic predictions.
Hyperbolic discounting Infographic
 libterm.com
libterm.com