Arrow's Impossibility Theorem reveals fundamental limitations in collective decision-making processes by proving that no voting system can simultaneously satisfy all fairness criteria when aggregating individual preferences. It highlights inherent conflicts between fairness conditions such as non-dictatorship, unanimity, and independence of irrelevant alternatives. Explore the rest of the article to understand how this theorem impacts voting systems and social choice theory.
Table of Comparison
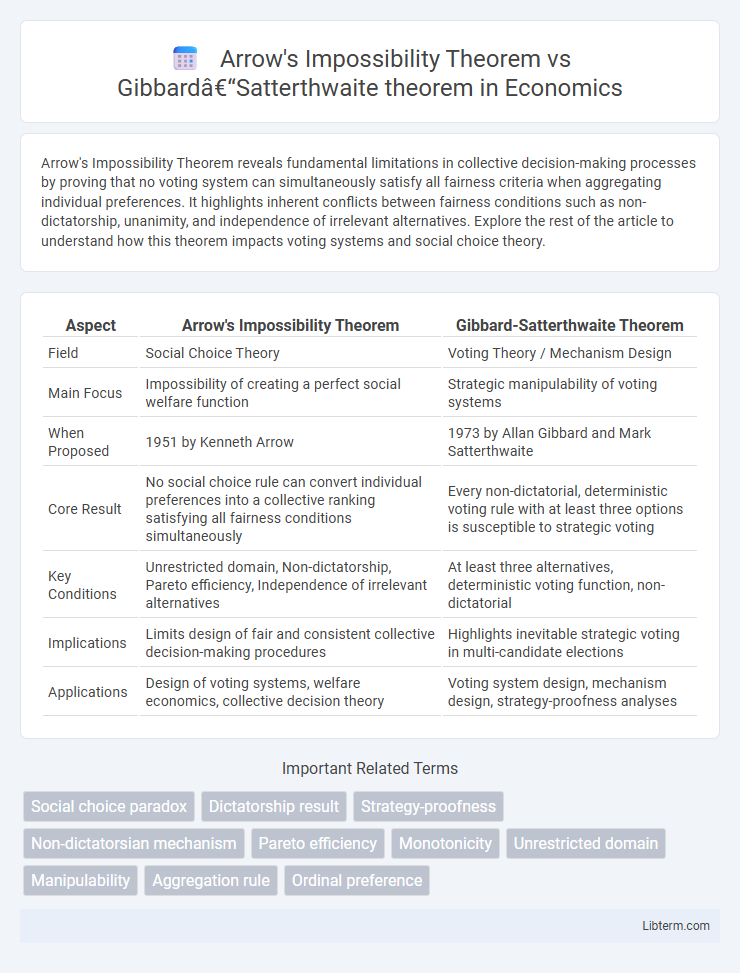
| Aspect | Arrow's Impossibility Theorem | Gibbard-Satterthwaite Theorem |
|---|---|---|
| Field | Social Choice Theory | Voting Theory / Mechanism Design |
| Main Focus | Impossibility of creating a perfect social welfare function | Strategic manipulability of voting systems |
| When Proposed | 1951 by Kenneth Arrow | 1973 by Allan Gibbard and Mark Satterthwaite |
| Core Result | No social choice rule can convert individual preferences into a collective ranking satisfying all fairness conditions simultaneously | Every non-dictatorial, deterministic voting rule with at least three options is susceptible to strategic voting |
| Key Conditions | Unrestricted domain, Non-dictatorship, Pareto efficiency, Independence of irrelevant alternatives | At least three alternatives, deterministic voting function, non-dictatorial |
| Implications | Limits design of fair and consistent collective decision-making procedures | Highlights inevitable strategic voting in multi-candidate elections |
| Applications | Design of voting systems, welfare economics, collective decision theory | Voting system design, mechanism design, strategy-proofness analyses |
Introduction to Social Choice Theory
Arrow's Impossibility Theorem highlights the inherent limitations in designing a social choice function that can convert individual preferences into a collective decision without violating key fairness criteria such as unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The Gibbard-Satterthwaite theorem extends this framework by demonstrating that any non-dictatorial voting mechanism with at least three possible outcomes is susceptible to strategic manipulation by voters. Both theorems are foundational in social choice theory, shaping the understanding of the trade-offs and challenges in aggregating individual preferences into a coherent, strategy-proof collective decision.
Overview of Arrow’s Impossibility Theorem
Arrow's Impossibility Theorem demonstrates that no social welfare function can simultaneously satisfy the criteria of unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives when aggregating individual preferences into a collective decision. This theorem highlights fundamental limitations in designing fair and consistent voting systems. Arrow's framework is foundational in social choice theory, influencing the understanding of collective decision-making constraints.
Key Concepts in Arrow’s Framework
Arrow's Impossibility Theorem centers on the impossibility of designing a social welfare function that simultaneously satisfies unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives. The theorem's key concepts emphasize the aggregation of individual preferences into a collective decision without violating fairness or rationality constraints. It highlights fundamental limitations in voting systems, contrasting with the Gibbard-Satterthwaite theorem that focuses on strategy-proofness and manipulability in voting mechanisms.
Overview of the Gibbard–Satterthwaite Theorem
The Gibbard-Satterthwaite theorem states that every non-dictatorial voting system with three or more options is susceptible to strategic voting or manipulation. This theorem highlights the inherent vulnerability in collective decision-making processes, where individuals can misrepresent preferences to achieve a more favorable outcome. It complements Arrow's Impossibility Theorem by emphasizing the limitations in designing fair and strategy-proof social choice mechanisms.
Core Assumptions Behind Each Theorem
Arrow's Impossibility Theorem assumes unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives in social welfare functions. Gibbard-Satterthwaite theorem requires at least three alternatives, strategy-proofness, and unilateral manipulation as core assumptions for individual voting rules. The fundamental difference rests in Arrow's focus on collective preference aggregation versus Gibbard-Satterthwaite's emphasis on manipulability in voting mechanisms.
Comparing Arrow’s and Gibbard–Satterthwaite’s Results
Arrow's Impossibility Theorem establishes that no voting system can simultaneously satisfy all fairness criteria like unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives when converting individual preferences into a collective decision. The Gibbard-Satterthwaite theorem complements this by proving that every non-dictatorial voting rule with three or more alternatives is susceptible to strategic manipulation or tactical voting. Together, these results highlight fundamental limitations in designing perfectly fair and strategy-proof voting systems.
Implications for Voting System Design
Arrow's Impossibility Theorem establishes that no voting system can simultaneously satisfy fairness criteria like unrestricted domain, non-dictatorship, Pareto efficiency, and independence of irrelevant alternatives, highlighting fundamental limitations in collective decision-making. The Gibbard-Satterthwaite theorem complements this by proving that every non-dictatorial voting system with three or more choices is susceptible to strategic voting, revealing inherent vulnerabilities to manipulation. These results imply that designing a perfect voting system is mathematically impossible, necessitating trade-offs between fairness, strategic resistance, and representativeness in election methods.
Limitations and Criticisms of Both Theorems
Arrow's Impossibility Theorem highlights the inherent limitations in creating a social welfare function that satisfies all fairness criteria simultaneously, revealing that no voting system can perfectly transform individual preferences into a collective decision without issues like dictatorial power or inconsistency. The Gibbard-Satterthwaite theorem exposes the inevitability of strategic voting, demonstrating that every non-dictatorial voting system with three or more choices can be manipulated by voters misrepresenting their true preferences. Both theorems face criticisms for their assumptions of unrestricted preference domains and strict rationality, which may not hold in real-world electoral systems, limiting their practical applicability.
Modern Applications and Extensions
Arrow's Impossibility Theorem underpins modern social choice theory by highlighting the challenges in creating fair voting systems that satisfy all desirable criteria simultaneously, influencing the design of electoral reform and collective decision-making algorithms. The Gibbard-Satterthwaite theorem extends these insights to strategic manipulation, proving that every non-dictatorial voting system with three or more alternatives can be susceptible to strategic voting, thereby shaping the development of mechanism design and incentive-compatible algorithms in modern political science and economics. Extensions of these theorems in computational social choice explore approximation methods and restricted preference domains to mitigate impossibility results, enabling practical applications in online voting platforms, multi-agent systems, and blockchain governance.
Conclusion: The Future of Social Choice Theory
Arrow's Impossibility Theorem and the Gibbard-Satterthwaite theorem both reveal fundamental limitations in designing fair and strategy-proof social choice mechanisms, demonstrating the inherent trade-offs in collective decision-making processes. These theorems underscore the challenges faced in achieving unanimous and manipulation-resistant voting systems, prompting ongoing research in computational social choice and mechanism design. Future advancements likely hinge on developing hybrid models or relaxing strict criteria to balance fairness, efficiency, and strategic resistance in practical applications.
Arrow's Impossibility Theorem Infographic
 libterm.com
libterm.com