Nash Equilibrium occurs when no player can improve their outcome by changing strategies while others keep theirs unchanged. This concept is fundamental in game theory, analyzing competitive situations where each participant's decision affects others. Discover how understanding Nash Equilibrium can enhance your strategic thinking by reading the rest of the article.
Table of Comparison
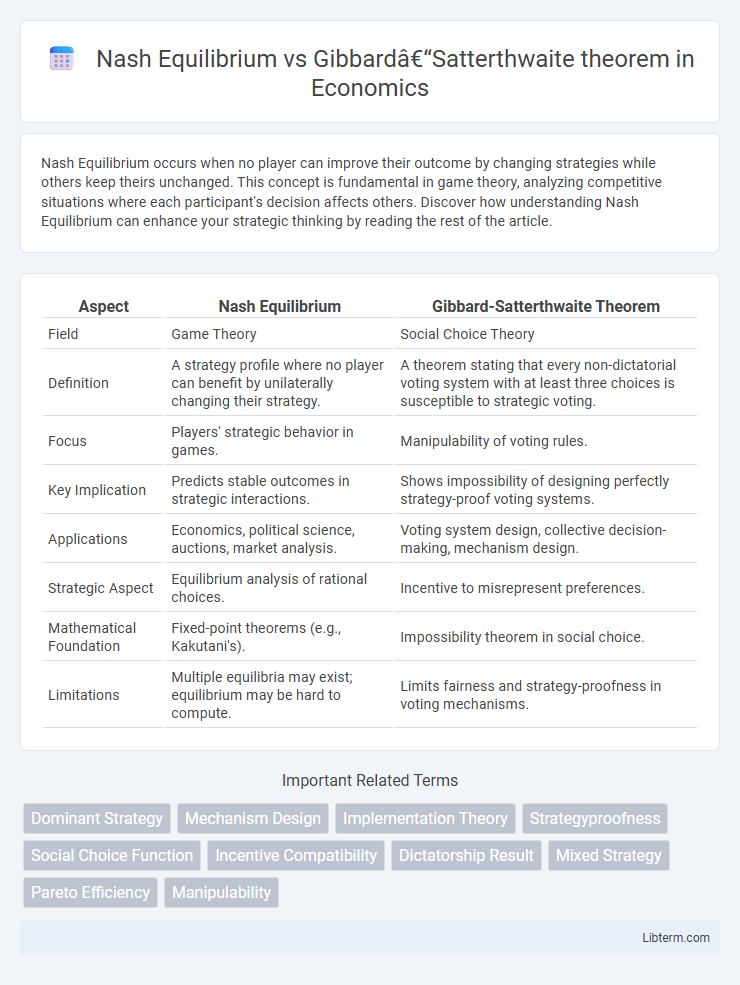
| Aspect | Nash Equilibrium | Gibbard-Satterthwaite Theorem |
|---|---|---|
| Field | Game Theory | Social Choice Theory |
| Definition | A strategy profile where no player can benefit by unilaterally changing their strategy. | A theorem stating that every non-dictatorial voting system with at least three choices is susceptible to strategic voting. |
| Focus | Players' strategic behavior in games. | Manipulability of voting rules. |
| Key Implication | Predicts stable outcomes in strategic interactions. | Shows impossibility of designing perfectly strategy-proof voting systems. |
| Applications | Economics, political science, auctions, market analysis. | Voting system design, collective decision-making, mechanism design. |
| Strategic Aspect | Equilibrium analysis of rational choices. | Incentive to misrepresent preferences. |
| Mathematical Foundation | Fixed-point theorems (e.g., Kakutani's). | Impossibility theorem in social choice. |
| Limitations | Multiple equilibria may exist; equilibrium may be hard to compute. | Limits fairness and strategy-proofness in voting mechanisms. |
Introduction to Game Theory and Social Choice
Nash Equilibrium represents a stable state in game theory where no player can improve their payoff by unilaterally changing strategies, emphasizing strategic decision-making in competitive scenarios. The Gibbard-Satterthwaite theorem in social choice theory asserts that every non-dictatorial voting system with three or more options is susceptible to strategic manipulation, highlighting limitations in collective decision mechanisms. Both concepts underpin fundamental challenges in predicting rational behavior within individual strategic interactions and group preference aggregation.
Defining Nash Equilibrium: Concepts and Applications
Nash Equilibrium is a fundamental concept in game theory where no player can improve their payoff by unilaterally changing strategies, given the strategies chosen by others. It applies broadly in economics, political science, and evolutionary biology to predict stable outcomes in strategic interactions without cooperative agreements. The Gibbard-Satterthwaite theorem, contrastingly, addresses social choice functions, proving that any non-dictatorial voting system with three or more options can be manipulated, underscoring the challenges in designing strategy-proof mechanisms.
The Gibbard–Satterthwaite Theorem Explained
The Gibbard-Satterthwaite theorem states that in any non-dictatorial voting system with three or more choices, it is impossible to design a strategy-proof mechanism that always produces a fair and truthful outcome, because voters can manipulate their preferences to achieve a more favorable result. This contrasts with Nash Equilibrium, where players' strategies stabilize because no one can gain by unilaterally changing their choice, but does not guarantee truthful revelation or fairness in voting contexts. The theorem highlights inherent limitations in collective decision-making mechanisms, emphasizing strategic vulnerability and the challenge of achieving both fairness and strategy-proofness simultaneously.
Mathematical Foundations: Assumptions and Frameworks
Nash Equilibrium is grounded in non-cooperative game theory, assuming rational players with complete knowledge of strategies and payoffs, leading to stable strategy profiles where no player can benefit from unilateral deviation. The Gibbard-Satterthwaite theorem, rooted in social choice theory and mechanism design, assumes at least three alternatives and non-dictatorial voting systems, proving that every non-manipulable voting rule must be dictatorial or manipulable. Both frameworks employ formal mathematical models, but Nash equilibrium relies on equilibrium concepts in strategic interactions, while Gibbard-Satterthwaite focuses on incentive compatibility and strategy-proofness in collective decision-making.
Incentive Compatibility in Games and Voting Systems
Nash Equilibrium ensures incentive compatibility in strategic games by stabilizing players' strategies so no one benefits from unilaterally deviating, while the Gibbard-Satterthwaite theorem highlights the challenge of incentive compatibility in voting systems by proving that every non-dictatorial voting mechanism with three or more options is vulnerable to strategic manipulation. The theorem demonstrates that no perfect voting rule exists to prevent voters from misrepresenting preferences, contrasting with the Nash Equilibrium's focus on equilibrium strategy profiles in games. Incentive compatibility remains a critical concern in designing mechanisms where truthful behavior aligns with individual optimal strategies.
Key Differences Between Nash Equilibrium and Gibbard–Satterthwaite
Nash Equilibrium is a solution concept in game theory where no player can benefit by unilaterally changing their strategy, emphasizing strategic stability in non-cooperative games. The Gibbard-Satterthwaite theorem addresses the impossibility of designing a voting system that is both strategy-proof and non-dictatorial when voters have three or more choices, focusing on preference aggregation and manipulation. The key difference lies in Nash Equilibrium's analysis of strategic interactions among rational players versus the Gibbard-Satterthwaite theorem's implication on the inherent manipulability of collective decision-making mechanisms.
Real-World Examples: Strategic Behavior and Manipulability
Nash Equilibrium captures the stable outcomes in strategic games where no player benefits from unilaterally changing their strategy, exemplified by firms in an oligopoly setting maintaining pricing strategies despite competitive pressure. The Gibbard-Satterthwaite theorem highlights the inevitability of manipulability in voting systems with three or more options, as seen in political elections where voters strategically misrepresent preferences to influence outcomes. These concepts underline the tension between strategic stability and the susceptibility of collective decision-making processes to strategic manipulation.
Implications for Mechanism Design
Nash Equilibrium ensures stable outcomes where no player benefits from unilateral deviation, providing a foundation for predicting strategic behavior in mechanism design. The Gibbard-Satterthwaite theorem reveals inherent limitations in designing voting mechanisms, showing that every non-dictatorial voting rule with three or more options is susceptible to strategic manipulation. Together, these concepts highlight the trade-offs in mechanism design between achieving equilibrium outcomes and preventing manipulation, guiding designers to create more robust and incentive-compatible systems.
Limitations and Criticisms of Both Theories
Nash Equilibrium faces limitations due to multiple equilibria and assumptions of perfect rationality, which often do not hold in real-world strategic interactions, leading to unpredictable or suboptimal outcomes. The Gibbard-Satterthwaite theorem highlights fundamental challenges in designing voting systems, showing that all non-dictatorial voting rules with three or more options are susceptible to strategic manipulation. Both theories face criticism for their idealized assumptions; Nash Equilibrium relies on common knowledge and rationality, while the Gibbard-Satterthwaite theorem assumes voters have complete information and deterministic preferences, restricting their practical applicability in complex social and economic systems.
Future Directions in Strategy and Social Choice Research
Exploring the intersection of Nash Equilibrium and the Gibbard-Satterthwaite theorem opens new avenues for designing strategy-proof mechanisms that incorporate equilibrium concepts to enhance collective decision-making. Future research aims to develop hybrid models that blend incentive compatibility with equilibrium stability, addressing challenges in multi-agent systems and voting protocols. Advancements in computational social choice and algorithmic game theory will drive innovations in robust, efficient mechanisms for social preferences aggregation under strategic behavior.
Nash Equilibrium Infographic
 libterm.com
libterm.com