Effective interest rate reflects the true cost of borrowing or return on investment by accounting for compounding periods within a year, offering a more accurate measure than nominal rates. Understanding this rate helps you make informed financial decisions, whether comparing loan options or evaluating savings accounts. Explore the rest of the article to learn how calculating the effective interest rate can optimize your financial strategy.
Table of Comparison
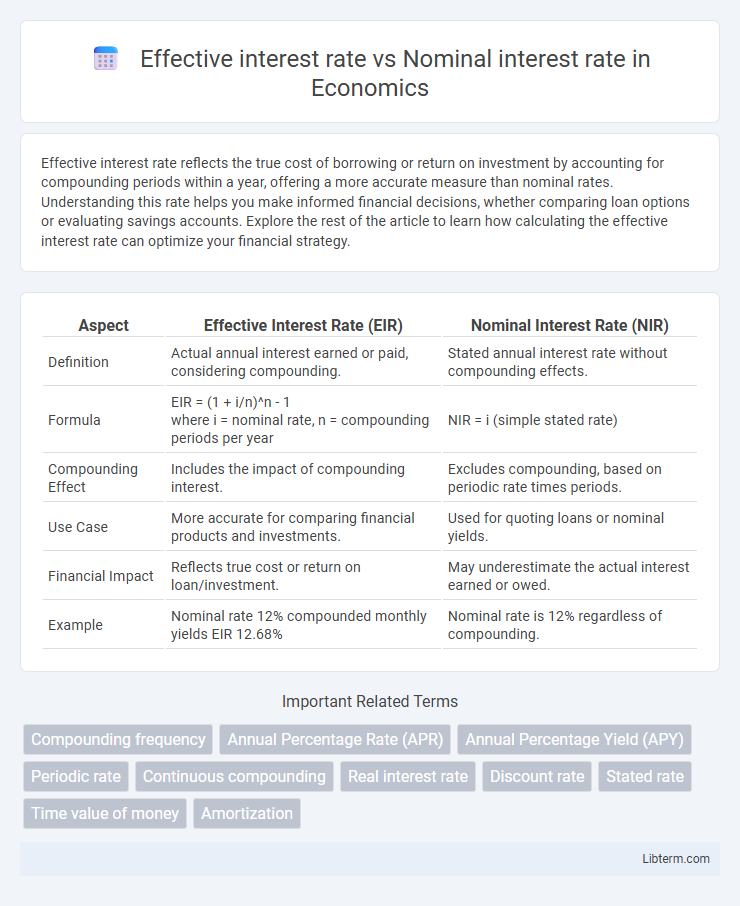
| Aspect | Effective Interest Rate (EIR) | Nominal Interest Rate (NIR) |
|---|---|---|
| Definition | Actual annual interest earned or paid, considering compounding. | Stated annual interest rate without compounding effects. |
| Formula | EIR = (1 + i/n)^n - 1 where i = nominal rate, n = compounding periods per year |
NIR = i (simple stated rate) |
| Compounding Effect | Includes the impact of compounding interest. | Excludes compounding, based on periodic rate times periods. |
| Use Case | More accurate for comparing financial products and investments. | Used for quoting loans or nominal yields. |
| Financial Impact | Reflects true cost or return on loan/investment. | May underestimate the actual interest earned or owed. |
| Example | Nominal rate 12% compounded monthly yields EIR 12.68% | Nominal rate is 12% regardless of compounding. |
Understanding Interest Rates: An Overview
Effective interest rate reflects the true cost of borrowing or the actual yield on investment by accounting for compounding periods within a year, while nominal interest rate represents the stated annual rate without compounding effects. Understanding the difference between effective and nominal rates is crucial for accurately comparing loans, savings accounts, or investment products. Effective interest rate is always equal to or higher than the nominal rate when compounding occurs more than once a year, providing a clearer picture of financial costs or gains.
What is Nominal Interest Rate?
Nominal interest rate represents the stated or face rate of interest on a loan or investment without accounting for compounding within the year. It is the percentage rate agreed upon by the lender and borrower, typically expressed on an annual basis, and does not reflect the effects of inflation or fees. Investors and borrowers use the nominal interest rate to understand basic cost or return but must consider the effective interest rate for a true measure of financial impact.
What is Effective Interest Rate?
Effective interest rate represents the true annual cost of borrowing or return on investment after accounting for compounding periods within a year, unlike the nominal interest rate which does not consider compounding effects. It provides a more accurate measure by incorporating the frequency of interest application, such as monthly or quarterly compounding, making it essential for comparing different financial products. Calculated using the formula (1 + nominal rate / n)^n - 1, where n is the number of compounding periods, the effective interest rate reflects the actual growth or cost of funds over a year.
Key Differences Between Nominal and Effective Interest Rates
The effective interest rate accounts for compounding periods within a year, reflecting the true cost of borrowing or yield on investment, while the nominal interest rate does not consider compounding and represents the stated annual rate. Effective interest rate is always equal to or higher than the nominal rate when compounding occurs more than once per year. Understanding the impact of compounding frequency is critical for accurate comparison of loans or investments based on nominal and effective rates.
How to Calculate Nominal Interest Rate
The nominal interest rate is calculated by dividing the annual percentage rate (APR) by the number of compounding periods per year, then multiplying by 100 to express it as a percentage. This rate does not account for compounding within the year, making it simpler but less precise than the effective interest rate. The formula for nominal interest rate is: Nominal Rate = APR / n, where n is the number of compounding periods annually.
How to Calculate Effective Interest Rate
The effective interest rate is calculated by compounding the nominal interest rate over the number of periods within a year using the formula: Effective Interest Rate = (1 + Nominal Rate / n)^n - 1, where n represents the number of compounding periods. This calculation accounts for interest-on-interest effects, providing a more accurate measure of the actual cost or yield of a financial product compared to the nominal interest rate, which does not consider compounding. Understanding the frequency of compounding (monthly, quarterly, annually) is essential for precisely determining the effective interest rate.
Impact of Compounding on Interest Rates
The effective interest rate accounts for the impact of compounding periods within a year, reflecting the true cost or yield of an investment, while the nominal interest rate is the stated annual rate without adjustment for compounding. Compounding frequency, such as monthly or quarterly, increases the effective rate above the nominal rate by accumulating interest on previously earned interest. Investors and borrowers use the effective interest rate to evaluate and compare financial products accurately, as it reveals the actual financial impact of interest accumulation over time.
Real-World Examples: Nominal vs. Effective Rates
The nominal interest rate represents the stated annual rate without adjustment for compounding, while the effective interest rate reflects the true annual cost or return accounting for compounding periods. For example, a credit card with a nominal rate of 12% compounded monthly results in an effective rate of approximately 12.68%, demonstrating how compounding increases the actual interest charged. Mortgage loans often quote nominal rates semi-annually but the effective rate captures the real cost, impacting borrowers' total payments and financial planning.
Why Effective Interest Rate Matters for Borrowers and Investors
Effective interest rate matters for borrowers and investors because it reflects the true cost or return of a loan or investment after accounting for compounding periods within a year. Unlike the nominal interest rate, which does not include the effects of compounding, the effective interest rate provides a more accurate measure of financial impact. This enables borrowers to assess the real expense of debt and allows investors to make informed decisions about the actual yield on their investments.
Choosing the Right Rate: Practical Tips and Considerations
Choosing the right interest rate involves comparing the effective interest rate, which accounts for compounding periods, with the nominal interest rate that reflects the stated annual rate without compounding effects. Prioritize the effective interest rate for a true cost of borrowing or actual investment return, since it provides a clearer financial picture for decision-making. Consider loan terms, compounding frequency, and fees to select the rate that aligns best with your financial goals and maximizes cost-efficiency or yield.
Effective interest rate Infographic
 libterm.com
libterm.com