The logit model is a powerful statistical tool used to predict the probability of a binary outcome based on one or more predictor variables. It estimates the relationship between the dependent variable and independent variables through the logistic function, making it ideal for classification problems. Explore the rest of the article to understand how the logit model can improve your predictive analytics skills.
Table of Comparison
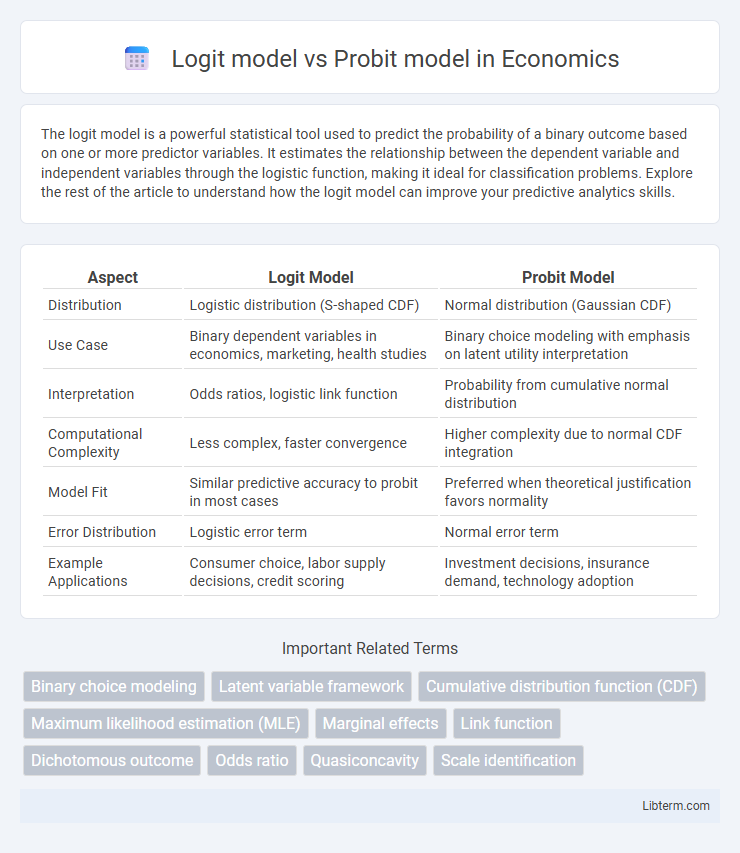
| Aspect | Logit Model | Probit Model |
|---|---|---|
| Distribution | Logistic distribution (S-shaped CDF) | Normal distribution (Gaussian CDF) |
| Use Case | Binary dependent variables in economics, marketing, health studies | Binary choice modeling with emphasis on latent utility interpretation |
| Interpretation | Odds ratios, logistic link function | Probability from cumulative normal distribution |
| Computational Complexity | Less complex, faster convergence | Higher complexity due to normal CDF integration |
| Model Fit | Similar predictive accuracy to probit in most cases | Preferred when theoretical justification favors normality |
| Error Distribution | Logistic error term | Normal error term |
| Example Applications | Consumer choice, labor supply decisions, credit scoring | Investment decisions, insurance demand, technology adoption |
Introduction to Logit and Probit Models
Logit and Probit models are widely used for modeling binary dependent variables in econometrics and statistics. The Logit model employs the logistic function to estimate the probability of a binary outcome, characterized by the log-odds being a linear combination of predictor variables. In contrast, the Probit model uses the standard normal cumulative distribution function to link predictors to the probability of an event, making it suitable for modeling latent variables with normally distributed errors.
Fundamental Concepts: Binary Choice Models
Logit and Probit models are fundamental binary choice models used to estimate the probability of a binary outcome based on predictor variables. The Logit model uses the logistic function to ensure predicted probabilities lie between 0 and 1, while the Probit model relies on the cumulative distribution function of the standard normal distribution. Both models address issues of non-linearity and heteroscedasticity in binary response data but differ in their distributional assumptions, with Logit assuming a logistic distribution and Probit assuming a normal distribution for the error terms.
Mathematical Formulations: Logit vs Probit
The Logit model uses the logistic function defined as \( P(Y=1|X) = \frac{1}{1 + e^{-\beta X}} \) to estimate the probability of a binary outcome, capturing the odds through a sigmoid curve. The Probit model employs the cumulative distribution function (CDF) of the standard normal distribution, expressed as \( P(Y=1|X) = \Phi(\beta X) \), where \( \Phi \) denotes the normal CDF, modeling the latent variable via a Gaussian process. Both models transform linear combinations of predictors into probabilities but differ in their link functions, with Logit implying a logistic distribution and Probit assuming a normal distribution for error terms.
Underlying Distributional Assumptions
The Logit model assumes a logistic distribution for the error terms, characterized by a cumulative distribution function (CDF) with heavier tails compared to the normal distribution. The Probit model is based on the assumption that the error terms follow a standard normal distribution, leading to a CDF with lighter tails and different sensitivity to data extremes. These underlying distributional assumptions influence the shape of the link functions and the interpretation of coefficients in binary outcome modeling.
Estimation Techniques and Model Fit
The Logit model uses the logistic distribution function and is estimated via Maximum Likelihood Estimation (MLE), optimizing the probability of observed outcomes through the logistic function. The Probit model relies on the standard normal cumulative distribution function and also applies MLE, fitting data with a probit link that assumes a latent normal variable. Both models assess goodness-of-fit using metrics like the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), and pseudo-R2, but the choice often depends on the distribution assumption and empirical fit to the data.
Interpretation of Coefficients
Logit model coefficients represent the change in the log-odds of the dependent event for a one-unit increase in the predictor variable, facilitating interpretation through odds ratios. Probit model coefficients indicate the change in the z-score of the standard normal distribution underlying the binary outcome, which requires normal CDF transformation for probability interpretation. Both models estimate probabilities differently but provide meaningful signs and significance levels to assess predictor impact on binary dependent variables.
Model Performance and Predictive Power
The Logit model employs a logistic distribution function, often providing robust predictive power with slightly better fit in datasets exhibiting non-linear relationships between variables, while the Probit model uses the cumulative normal distribution and may better capture subtler variations in error terms. Model performance comparison typically hinges on likelihood-based metrics such as Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), with Logit favored in cases with larger sample sizes and Probit in scenarios assuming normally distributed errors. Predictive accuracy, evaluated through measures like the Area Under the Receiver Operating Characteristic Curve (AUC-ROC), often reveals comparable results, though Logit's interpretability in odds ratios can enhance practical decision-making.
Practical Applications in Real-World Scenarios
Logit and Probit models are commonly used for binary outcome predictions in fields such as finance, healthcare, and marketing. The Logit model is preferred in credit scoring and customer purchase decisions due to its interpretability and ease of calculation. The Probit model is favored in toxicology and social sciences where underlying latent variables follow a normal distribution, enhancing model fit and inference accuracy.
Advantages and Limitations of Each Model
The Logit model offers easier interpretation through odds ratios and handles large samples efficiently, but it assumes a logistic distribution which may not fit all datasets well. The Probit model, based on the normal distribution, is advantageous when modeling latent variables and provides smoother probability curves, yet it is computationally more complex and harder to interpret than Logit. Both models serve binary outcome prediction but differ in error distribution assumptions, impacting their applicability depending on the nature of the data and the research context.
Choosing Between Logit and Probit: Key Considerations
Choosing between Logit and Probit models depends largely on the underlying distribution assumption of the error term; Logit uses the logistic distribution while Probit assumes a normal distribution. The Logit model often provides easier interpretation through odds ratios and is preferred in cases requiring straightforward probability modeling. Probit is favored when latent variables or cumulative normal distribution characteristics are better suited to the data, particularly in econometrics and psychometrics.
Logit model Infographic
 libterm.com
libterm.com