The mass moment of inertia measures an object's resistance to rotational acceleration about a specific axis, depending on how its mass is distributed relative to that axis. Calculating this property accurately is crucial for analyzing the dynamics of rotating systems in engineering and physics. Discover how understanding mass moment of inertia can optimize your mechanical design by reading the rest of the article.
Table of Comparison
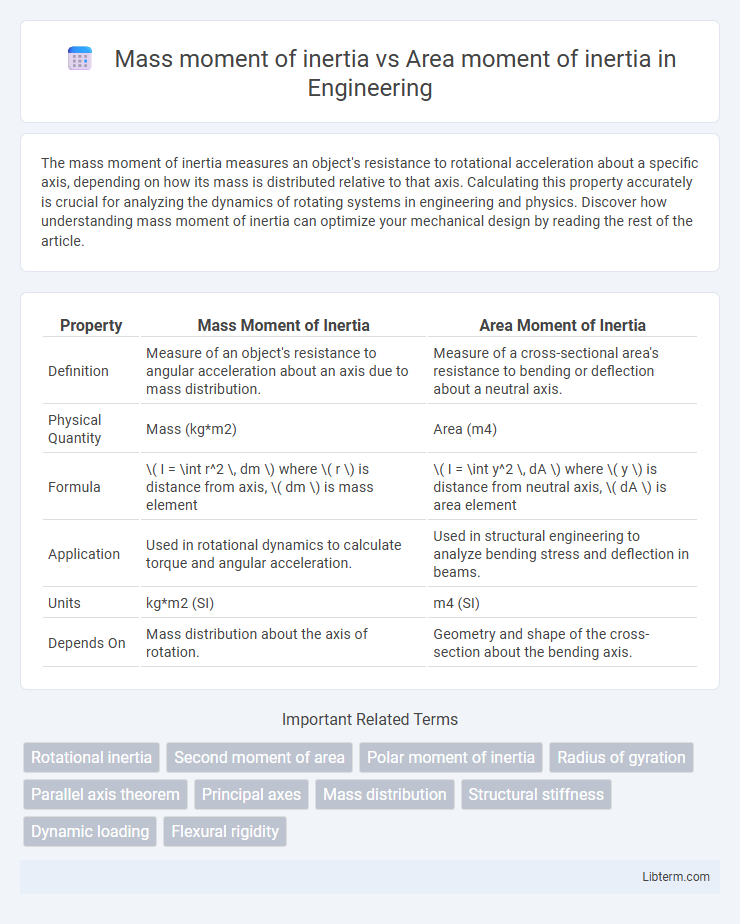
| Property | Mass Moment of Inertia | Area Moment of Inertia |
|---|---|---|
| Definition | Measure of an object's resistance to angular acceleration about an axis due to mass distribution. | Measure of a cross-sectional area's resistance to bending or deflection about a neutral axis. |
| Physical Quantity | Mass (kg*m2) | Area (m4) |
| Formula | \( I = \int r^2 \, dm \) where \( r \) is distance from axis, \( dm \) is mass element | \( I = \int y^2 \, dA \) where \( y \) is distance from neutral axis, \( dA \) is area element |
| Application | Used in rotational dynamics to calculate torque and angular acceleration. | Used in structural engineering to analyze bending stress and deflection in beams. |
| Units | kg*m2 (SI) | m4 (SI) |
| Depends On | Mass distribution about the axis of rotation. | Geometry and shape of the cross-section about the bending axis. |
Introduction to Moments of Inertia
Mass moment of inertia quantifies an object's resistance to angular acceleration around an axis, depending on mass distribution relative to that axis. Area moment of inertia measures a cross-section's resistance to bending and deflection, related to geometry and dimensions of structural elements. Understanding these distinct moments of inertia is crucial in mechanical engineering and structural analysis for optimizing design and stability.
Defining Mass Moment of Inertia
Mass moment of inertia quantifies an object's resistance to angular acceleration based on its mass distribution relative to the axis of rotation. It is calculated by integrating the product of the mass elements and the square of their distances from the rotation axis, expressed in units like kg*m2. Unlike area moment of inertia, which pertains to the geometric distribution of an object's cross-sectional area and its resistance to bending, mass moment of inertia directly relates to dynamic rotational properties.
Understanding Area Moment of Inertia
Area moment of inertia, also known as the second moment of area, quantifies a beam's resistance to bending and deflection, crucial for structural engineering and design. Unlike mass moment of inertia, which relates to an object's rotational dynamics and depends on mass distribution, area moment of inertia is purely geometric and calculated based on cross-sectional shape and area. Understanding area moment of inertia enables engineers to predict bending stresses and optimize shapes for maximum strength and minimal material usage in beams, columns, and other structural elements.
Physical Significance: Mass vs Area Moment
Mass moment of inertia quantifies an object's resistance to angular acceleration based on mass distribution relative to an axis, crucial in dynamics and rotational motion analysis. Area moment of inertia, or second moment of area, measures a cross-section's ability to resist bending and deflection under load, fundamental in structural engineering and beam theory. While mass moment of inertia relates to how mass affects rotational behavior, area moment of inertia focuses on geometric properties influencing structural stiffness.
Mathematical Formulations and Units
Mass moment of inertia (I) is mathematically formulated as \( I = \int r^2 dm \), where \( r \) is the distance from the axis of rotation and \( dm \) is the differential mass element, measured in \( \text{kg*m}^2 \). Area moment of inertia (also called the second moment of area) is defined as \( I = \int y^2 dA \), where \( y \) is the distance from the neutral axis and \( dA \) is the differential area element, with units of \( \text{m}^4 \). While mass moment of inertia quantifies an object's resistance to angular acceleration, area moment of inertia measures a beam's resistance to bending.
Applications of Mass Moment of Inertia
Mass moment of inertia plays a crucial role in mechanical engineering and aerospace applications by quantifying an object's resistance to angular acceleration around an axis, essential for designing rotating machinery, vehicle dynamics, and robotic arms. It is used extensively in the analysis of flywheels, turbines, and gyroscopes to ensure stability and efficient energy transfer. Unlike the area moment of inertia, which is primarily applied in structural engineering to predict bending and deflection in beams and columns, the mass moment of inertia is focused on dynamic systems involving rotational motion.
Applications of Area Moment of Inertia
Area moment of inertia, also known as the second moment of area, is crucial in structural engineering for analyzing bending and deflection of beams under loads, determining the stiffness and resistance to bending in beams, shafts, and other structural elements. It is widely used in the design of bridges, buildings, and mechanical components to ensure stability and safety by minimizing deformation. In contrast, mass moment of inertia applies primarily to rotational dynamics and governs how an object resists angular acceleration about an axis, making it essential in mechanical systems involving rotation.
Key Differences between Mass and Area Moments
Mass moment of inertia quantifies an object's resistance to rotational acceleration about an axis and depends on the mass distribution relative to that axis, expressed in kg*m2. Area moment of inertia, also known as the second moment of area, measures a cross-section's resistance to bending and is calculated based on geometric shape and dimensions, expressed in m^4. Key differences include mass moment of inertia involving mass and rotational dynamics, while area moment of inertia involves sectional geometry and structural bending stresses.
Common Misconceptions and Clarifications
Mass moment of inertia quantifies an object's resistance to angular acceleration based on mass distribution relative to an axis, while area moment of inertia measures a beam's resistance to bending based on its cross-sectional shape. A common misconception is confusing these two properties because both use the term "moment of inertia," but they apply to different physical phenomena: mass moment relates to rotational dynamics, and area moment pertains to structural analysis. Clarifying their units--mass moment of inertia in kg*m2 and area moment of inertia in m4--helps distinguish their distinct roles in mechanics and engineering.
Summary and Practical Insights
Mass moment of inertia measures an object's resistance to angular acceleration based on mass distribution relative to an axis, essential for dynamic analysis in mechanical systems. Area moment of inertia quantifies a cross-sectional shape's resistance to bending and deflection, critical for structural engineering and beam design. Understanding both concepts aids in optimizing mechanical performance and structural integrity by accurately predicting rotational dynamics and stress distribution.
Mass moment of inertia Infographic
 libterm.com
libterm.com