The Rankine cycle is a fundamental thermodynamic process used to convert heat into mechanical work, predominantly in steam power plants. It involves the expansion of steam through a turbine, condensation in a condenser, and pumping of liquid water back to the boiler, optimizing energy efficiency. Explore this article to understand the detailed workings and applications of the Rankine cycle in power generation.
Table of Comparison
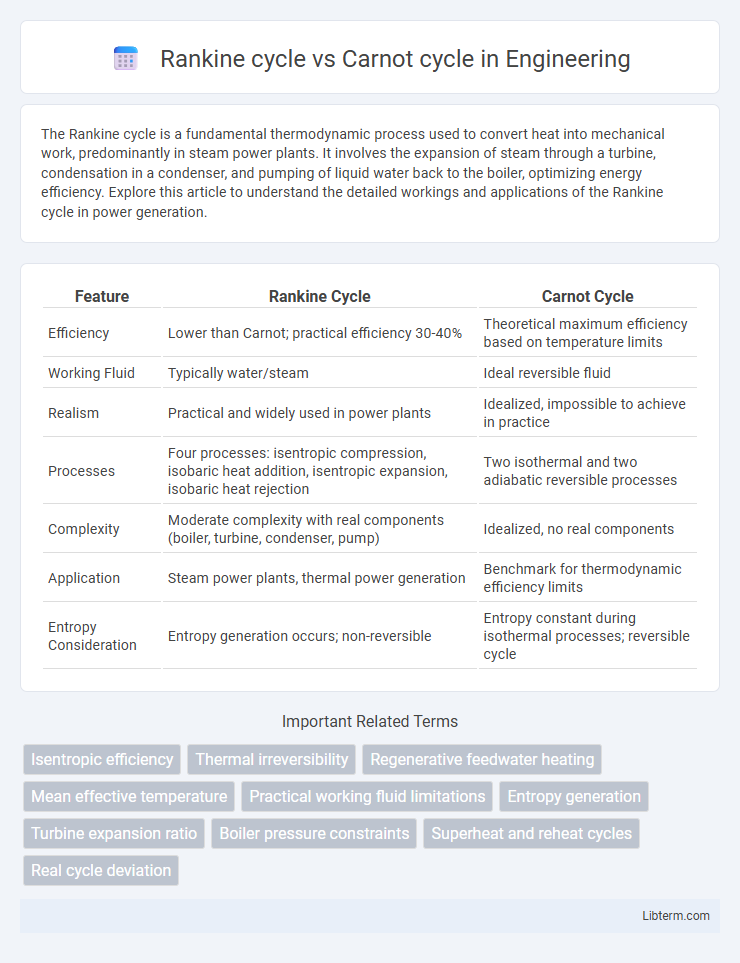
| Feature | Rankine Cycle | Carnot Cycle |
|---|---|---|
| Efficiency | Lower than Carnot; practical efficiency 30-40% | Theoretical maximum efficiency based on temperature limits |
| Working Fluid | Typically water/steam | Ideal reversible fluid |
| Realism | Practical and widely used in power plants | Idealized, impossible to achieve in practice |
| Processes | Four processes: isentropic compression, isobaric heat addition, isentropic expansion, isobaric heat rejection | Two isothermal and two adiabatic reversible processes |
| Complexity | Moderate complexity with real components (boiler, turbine, condenser, pump) | Idealized, no real components |
| Application | Steam power plants, thermal power generation | Benchmark for thermodynamic efficiency limits |
| Entropy Consideration | Entropy generation occurs; non-reversible | Entropy constant during isothermal processes; reversible cycle |
Introduction to Thermodynamic Cycles
The Rankine cycle, commonly used in power plants, converts heat into mechanical work by vaporizing water and condensing steam in a closed loop, emphasizing practical efficiency under real-world constraints. The Carnot cycle, an idealized thermodynamic model, defines the maximum possible efficiency between two temperature reservoirs through reversible processes but is not realizable in practical applications. Understanding both cycles is crucial for optimizing energy conversion and improving the design of thermal engines.
Overview of the Carnot Cycle
The Carnot cycle represents an idealized thermodynamic process that operates between two heat reservoirs at constant temperatures, achieving maximum efficiency dictated by the temperature difference. It consists of two isothermal processes and two adiabatic processes, forming a reversible cycle with no entropy generation. This theoretical model provides a benchmark for the maximum achievable efficiency in heat engines, guiding the evaluation of real cycles like the Rankine cycle.
Fundamentals of the Rankine Cycle
The Rankine cycle operates on the principle of converting heat into mechanical work using phase changes of a working fluid, typically water, through four main processes: isentropic compression, constant pressure heat addition, isentropic expansion, and constant pressure heat rejection. Unlike the ideal Carnot cycle, the Rankine cycle is more practical for real-world applications such as steam power plants because it accounts for realistic fluid properties and phase changes. Thermal efficiency of the Rankine cycle depends on factors like boiler and condenser temperatures, turbine and pump efficiencies, and the working fluid's thermodynamic properties.
Key Differences Between Rankine and Carnot Cycles
The Rankine cycle operates using phase change of the working fluid, typically water, between liquid and vapor, making it practical for real-world power plants, whereas the Carnot cycle is an idealized thermodynamic cycle with reversible processes and no phase change, representing maximum theoretical efficiency. The Rankine cycle includes components such as a boiler, turbine, condenser, and pump, with irreversibilities like friction and heat losses affecting performance, while the Carnot cycle consists of two isothermal and two adiabatic processes with no losses. Efficiency of the Rankine cycle is lower due to practical constraints, whereas the Carnot cycle efficiency depends solely on the temperature difference between the heat source and sink, serving as an upper limit for heat engine performance.
Efficiency Comparison: Rankine vs Carnot
The Rankine cycle typically achieves lower thermal efficiency compared to the Carnot cycle due to practical irreversibilities like friction, heat losses, and non-ideal component behavior, which reduce work output. While the Carnot cycle represents the theoretical maximum efficiency based on operating temperatures, its idealized isentropic processes and perfect heat exchange are unattainable in real systems. Engineering efforts to improve Rankine cycle efficiency focus on superheating, reheating, and regenerative feedwater heating to approach but never exceed the Carnot efficiency limit determined by the temperature difference between the heat source and sink.
Practical Applications of Rankine Cycle
The Rankine cycle is widely employed in practical power generation systems such as steam turbines in thermal power plants due to its ability to efficiently convert heat energy into mechanical work under realistic operating conditions. Unlike the idealized Carnot cycle, which is limited by its reversible processes and impractical assumptions, the Rankine cycle accommodates phase change of water, enabling effective use of low-grade heat sources and cycling between liquid and vapor states. Its adaptability and integration with real-world equipment make it the preferred choice for electricity production in coal, nuclear, and solar thermal power plants.
Limitations and Challenges of Carnot Cycle
The Carnot cycle, while theoretically the most efficient heat engine operating between two temperatures, faces significant practical limitations such as the requirement for reversible processes and zero entropy generation, which are impossible to achieve in real engines. Its idealized assumptions, including perfect insulation and infinitely slow heat transfer, make it impractical for actual power plants where irreversibilities, friction, and finite-rate heat transfer dominate. Consequently, the Rankine cycle is preferred in engineering due to its ability to model realistic steam power systems with components like turbines, condensers, and pumps, accommodating real fluid behaviors and operating conditions.
Real-World Factors Affecting Both Cycles
The Rankine cycle experiences efficiency losses due to pump and turbine irreversibilities, pressure drops, and non-ideal heat transfer, while the Carnot cycle, though theoretically more efficient, is impractical because it requires reversible processes and perfectly adiabatic conditions. Real-world constraints such as fluid friction, mechanical wear, and finite heat source temperatures reduce the achievable performance of both cycles. In industrial applications, the Rankine cycle remains dominant for power generation despite lower efficiencies because of its adaptability and fewer practical limitations compared to the idealized Carnot cycle.
Innovations and Improvements in Rankine Cycle
The Rankine cycle incorporates innovations such as superheating, reheating, and regeneration to enhance thermal efficiency beyond the idealized Carnot cycle under practical conditions. Superheating increases the average temperature during heat addition, while reheating reduces moisture content in the turbine, improving moisture-related performance issues. Regenerative feedwater heating recovers waste heat, raising the cycle's overall efficiency and enabling more effective energy conversion in real-world power plants.
Conclusion: Selecting the Optimal Thermodynamic Cycle
The Rankine cycle offers practical advantages for power generation due to its real-world efficiency and ability to handle phase changes, unlike the idealized Carnot cycle, which serves as a theoretical maximum efficiency benchmark. Engineers select the Rankine cycle for its balance between achievable efficiency and feasibility in steam power plants, while the Carnot cycle remains a standard for comparing thermodynamic performance limits. Optimal cycle selection hinges on application-specific factors such as operational conditions, working fluid properties, and economic considerations.
Rankine cycle Infographic
 libterm.com
libterm.com