Reynolds analogy provides a fundamental relationship between heat transfer and momentum transfer in fluid flow, allowing engineers to predict convective heat transfer coefficients based on known friction factors. This analogy simplifies complex thermal and fluid dynamics problems by linking the Nusselt number to the Reynolds and Prandtl numbers, aiding in efficient design of heat exchangers and aerodynamic surfaces. Explore the rest of the article to deepen your understanding of Reynolds analogy and its practical applications in engineering.
Table of Comparison
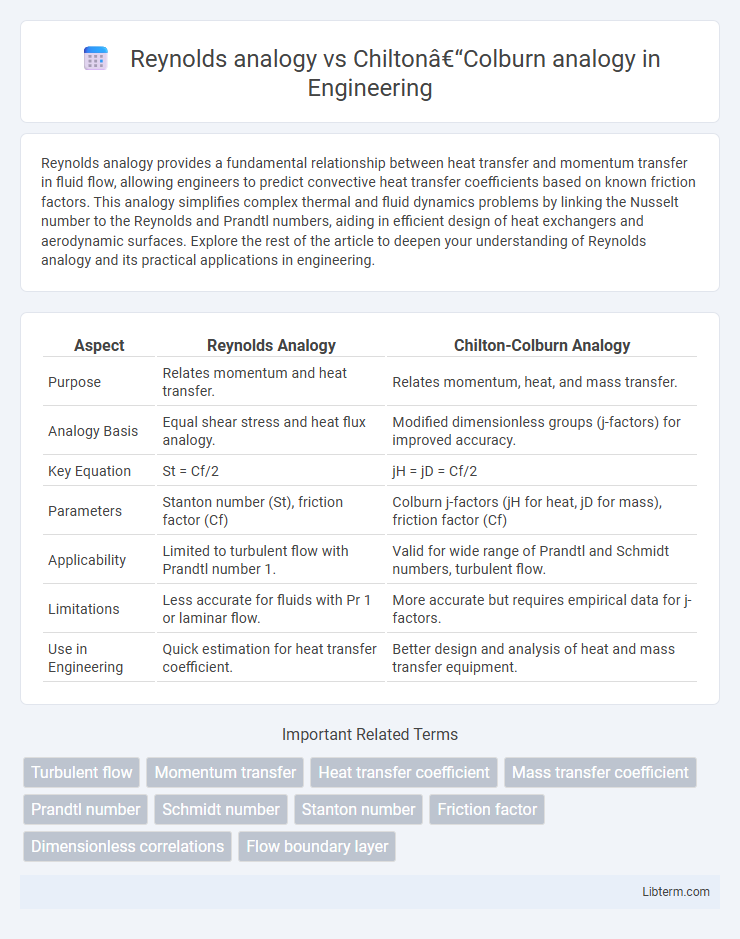
| Aspect | Reynolds Analogy | Chilton-Colburn Analogy |
|---|---|---|
| Purpose | Relates momentum and heat transfer. | Relates momentum, heat, and mass transfer. |
| Analogy Basis | Equal shear stress and heat flux analogy. | Modified dimensionless groups (j-factors) for improved accuracy. |
| Key Equation | St = Cf/2 | jH = jD = Cf/2 |
| Parameters | Stanton number (St), friction factor (Cf) | Colburn j-factors (jH for heat, jD for mass), friction factor (Cf) |
| Applicability | Limited to turbulent flow with Prandtl number 1. | Valid for wide range of Prandtl and Schmidt numbers, turbulent flow. |
| Limitations | Less accurate for fluids with Pr 1 or laminar flow. | More accurate but requires empirical data for j-factors. |
| Use in Engineering | Quick estimation for heat transfer coefficient. | Better design and analysis of heat and mass transfer equipment. |
Introduction to Heat and Mass Transfer Analogies
Reynolds analogy establishes a fundamental relationship between momentum and heat transfer by equating the dimensionless shear stress and heat transfer coefficients, primarily applicable in turbulent flow with Prandtl number near unity. Chilton-Colburn analogy extends this concept by incorporating mass transfer, introducing the j-factors (j_H for heat, j_D for mass, and j_f for friction) to generalize heat, mass, and momentum transfer correlations across varying fluid properties and flow conditions. These analogies enable engineers to predict heat and mass transfer rates from momentum transfer measurements, enhancing design accuracy in convective heat exchanger and chemical reactor applications.
Overview of Reynolds Analogy
Reynolds Analogy relates momentum and heat transfer by assuming equal turbulent diffusivities for momentum and heat, simplifying the calculation of heat transfer coefficients from friction factors. It is most accurate in turbulent flow regimes with Prandtl numbers close to unity, where thermal and momentum boundary layers behave similarly. Compared to Chilton-Colburn analogy, Reynolds analogy provides a more straightforward but less precise estimation, as it neglects differences in thermal and momentum diffusivities.
Fundamentals of Chilton–Colburn Analogy
The Chilton-Colburn analogy extends the Reynolds analogy by incorporating dimensionless groups such as the Colburn j-factors, which relate heat, mass, and momentum transfer more accurately for turbulent flow conditions. This analogy is based on the principle that the mechanisms governing momentum, heat, and mass transfer exhibit similar behaviors when expressed through corresponding dimensionless parameters. It provides a more precise correlation for convective heat transfer coefficients by linking them with friction factors and Schmidt or Prandtl numbers, improving predictive consistency in engineering applications.
Mathematical Formulations: Reynolds vs Chilton–Colburn
The Reynolds analogy mathematically simplifies heat transfer and momentum transfer by equating the Stanton number (St) to half the skin friction coefficient (Cf/2), assuming Prandtl number (Pr) of unity, expressed as St = Cf/2. The Chilton-Colburn analogy refines this approach by introducing the j-factor, representing dimensionless heat transfer (jH) and mass transfer (jD) coefficients, formulated as jH = St Pr2/3 and equated to Cf/2, accounting for variable Prandtl numbers. Both analogies aim to relate turbulent heat, mass, and momentum transfer, with Chilton-Colburn providing improved accuracy for non-unity Prandtl and Schmidt numbers through its modified mathematical expressions.
Underlying Assumptions of Both Analogies
Reynolds analogy assumes equal momentum and heat transfer coefficients by considering turbulent flow with a Prandtl number of unity, implying identical velocity and thermal boundary layers. Chilton-Colburn analogy extends this by introducing a correction factor, the j-factor, to account for non-unity Prandtl numbers and differences in velocity and thermal boundary layer thicknesses. Both analogies rely on the premise of turbulent flow and dominant convective transport mechanisms but differ in their treatment of fluid properties and boundary layer characteristics.
Applicability and Limitations
The Reynolds analogy is primarily applicable for turbulent flow with a Prandtl number near unity, simplifying heat and momentum transfer correlations by assuming equal turbulent diffusivities. The Chilton-Colburn analogy extends applicability to a broader range of Prandtl and Schmidt numbers, improving accuracy in convective heat and mass transfer predictions for both laminar and turbulent regimes. Limitations of the Reynolds analogy include its inaccuracy for fluids with Prandtl numbers significantly different from one, while the Chilton-Colburn analogy may still oversimplify complex flow phenomena such as strong buoyancy effects or non-Newtonian fluids.
Comparative Analysis: Accuracy and Use Cases
Reynolds analogy provides a simplified correlation between momentum and heat transfer by assuming equal turbulent Prandtl and Schmidt numbers, making it less accurate for fluids with varying thermal and mass diffusivities. Chilton-Colburn analogy introduces correction factors (j-factors) that account for differences in thermal and mass diffusivities, resulting in improved accuracy across a broader range of Reynolds, Prandtl, and Schmidt numbers. Reynolds analogy is commonly used for quick estimates in high-turbulence flows with similar momentum and heat transfer characteristics, while Chilton-Colburn analogy is preferred in detailed heat exchanger design and chemical process engineering where precise transfer coefficients are essential.
Relevance in Modern Engineering Applications
Reynolds analogy simplifies heat and momentum transfer by assuming similar turbulent mechanisms, making it useful for quick estimates in aerodynamic and heat exchanger design. Chilton-Colburn analogy extends this by incorporating mass transfer and empirical corrections, enhancing accuracy for chemical reactors and process engineering. Modern engineering increasingly favors Chilton-Colburn models due to their better prediction capabilities across varying Reynolds numbers and fluid properties, supporting optimized thermal management and energy efficiency.
Practical Examples in Industrial Processes
Reynolds analogy simplifies heat and momentum transfer analysis by assuming similar mechanisms, commonly used in turbulent pipe flow for estimating convective heat transfer in process industries. Chilton-Colburn analogy extends this by incorporating empirical correction factors, offering more accurate predictions in applications like chemical reactors and air conditioning systems where mass transfer also plays a critical role. Both analogies facilitate design and optimization of heat exchangers and cooling systems, with Chilton-Colburn preferred for its versatility in complex industrial processes involving simultaneous heat, mass, and momentum transfer.
Conclusion: Choosing the Right Analogy
Reynolds analogy is suitable for simple, turbulent flow situations where heat and momentum transfer have similar mechanisms, providing a quick, approximate relation between friction and heat transfer coefficients. Chilton-Colburn analogy offers greater accuracy by incorporating dimensionless groups like the Colburn factor, making it preferable for complex flows and detailed heat transfer analysis. Choosing the right analogy depends on the required precision and flow characteristics, with Chilton-Colburn being favored in engineering applications demanding higher reliability.
Reynolds analogy Infographic
 libterm.com
libterm.com